Fig.1.22 shows two blocks of masses m1=3kgandm2=5kg, both moving towards right on a frictionless surface with speeds u1=10m⋅s−1andu2=4m⋅s−1 respectively. To the back side of m2 an ideal spring fo force constant 1000N⋅m−1 is attached. Calculate the maximum compression of the spring when the blocks collide ?

m1=3kg,m2=5kg
u1=10m⋅s−1,u2=4m⋅s−1
Force constant , k=1000N⋅m−1
Let v be the speed of the combination.
Using the law of conservation of linear momentum,
m1u1+m2u2=(m1+m2)v
∴v=m1u1+m2u2m1+m2=3×10+5×43+5=6.25m⋅s−1
Also, let x be the maximum compression of the spring when the blocks collide.
∴ From conservation of mechanical energy , we get
12m1u21+12m2u22=12(m1+m2)v2+12kx2
or,500x2=380−312.5=67.5
∴x=√67.5500≈0.367m
Topper's Solved these Questions
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - SECTION RELATED QUESTIONS
24 Videos
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
38 Videos
- WBCHSE QUESTION PAPER -2019BOOK - CHHAYA PUBLICATIONCHAPTER - WBCHSE QUESTION PAPER -2019EXERCISE - SECTION - II ( GROUP -D)
10 Videos
Similar Questions
Two blocks of masses m1=2kg and m2=5 kg are moving in the same direction along a frictionless surface with speeds 10m/s and 3m/s, respectively, m2 being ahead of m1. An ideal spring with k=1120N/m is attached to the back side of m2. Find the maximum compression of the spring when the blocks collide. What are the final velocities of the blocks when they separate?
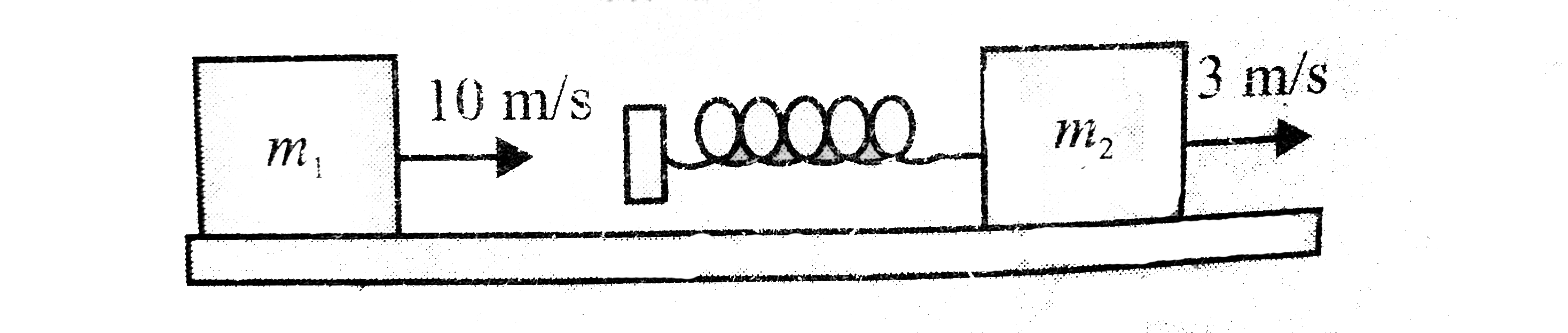
View SolutionTwo blocks of masses m1=2kg and m2=5 kg are moving in the same direction along a frictionless surface with speeds 10m/s and 3m/s, respectively, m2 being ahead of m1. An ideal spring with k=1120N/m is attached to the back side of m2. Find the maximum compression of the spring when the blocks collide. What are the final velocities of the blocks when they separate?
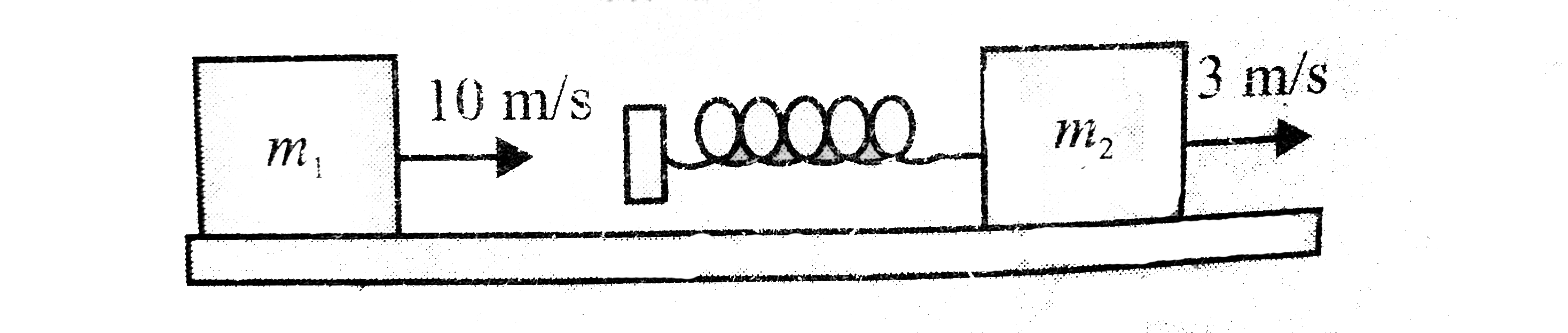
View Solution
Knowledge Check
Two blocks of masses m1=2kg and m2=4kg are moving in the same direction with speeds v1=6m/s and v2=3m/s, respectively on a frictionless surface as shown in the figure. An ideal spring with spring constant k=30000N/m is attached to the back side of m2. Then the maximum compression of the spring after collision will be
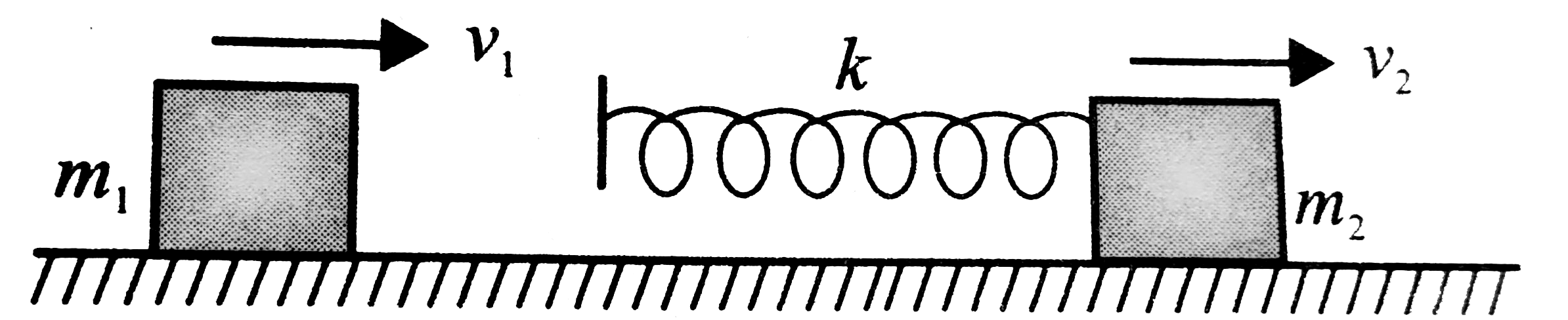 A0.06mB0.04mC0.02mDnone of these
A0.06mB0.04mC0.02mDnone of theseA mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
A0.15 mB0.12 mC1.5 mD0.5 m
Two blocks of masses m1=2kg and m2=4kg are moving in the same direction with speeds v1=6m/s and v2=3m/s, respectively on a frictionless surface as shown in the figure. An ideal spring with spring constant k=30000N/m is attached to the back side of m2. Then the maximum compression of the spring after collision will be
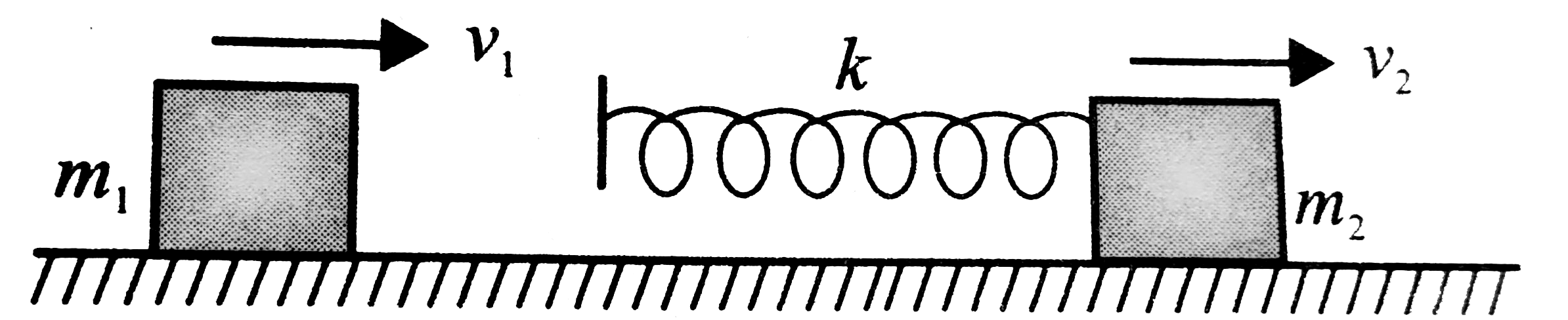
View SolutionA 4.0 kg body, moving with a speed of 2.0m/s ,collides with a spring bumper of negligible mass and force constant 100Nm−1 .The maximum compression of the spring is ?
View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.

View SolutionA block of mass 2 kg is moving on a frictionless horizontal surface with a velocity of 1m/s towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100N/m. Find the rnaximum compression of the spring
View SolutionFind the loss of KE of the two particles of mass m1=3kg&m2=6kg, moving towards each other with speed u1=5m/s,u2=10m/s respectively. The coefficient of restitution of collision of the particles is e = 0.5.
View SolutionFind the loss of KE of the two particles of mass m1=3kg&m2=6kg, moving towards each other with speed u1=5m/s,u2=10m/s respectively. The coefficient of restitution of collision of the particles is e = 0.5.
View Solution
