Find the loss of KE of the two particles of mass m1=3kg&m2=6kg, moving towards each other with speed u1=5m/s,u2=10m/s respectively. The coefficient of restitution of collision of the particles is e = 0.5.
The correct Answer is:169 J
To find the loss of kinetic energy (KE) of two particles during a collision, we will follow these steps:
Step 1: Calculate Initial Kinetic Energy
The initial kinetic energy (KE_initial) of the two particles can be calculated using the formula:
KE=12mu2
where m is the mass and u is the initial velocity.
For particle 1 (mass m1=3kg, velocity u1=5m/s):
KE1=12×3×(5)2=12×3×25=37.5J
For particle 2 (mass m2=6kg, velocity u2=10m/s):
KE2=12×6×(10)2=12×6×100=300J
Thus, the total initial kinetic energy is:
KEinitial=KE1+KE2=37.5+300=337.5J
Step 2: Apply Conservation of Momentum
The total momentum before and after the collision must be conserved. The initial momentum pinitial is given by:
pinitial=m1u1+m2(−u2)=3×5+6×(−10)=15−60=−45kg m/s
Let V1 and V2 be the final velocities of masses m1 and m2 respectively. The final momentum pfinal is:
pfinal=m1V1+m2V2
Setting pinitial=pfinal:
3V1+6V2=−45(Equation 1)
Step 3: Use Coefficient of Restitution
The coefficient of restitution e relates the velocities before and after the collision:
e=V2−V1u1+u2
Given e=0.5, u1=5, and u2=10:
0.5=V2−V15+10=V2−V115
Thus,
V2−V1=0.5×15=7.5(Equation 2)
Step 4: Solve the Equations
Now we have two equations:
1. 3V1+6V2=−45
2. V2−V1=7.5
From Equation 2, we can express V2 in terms of V1:
V2=V1+7.5
Substituting into Equation 1:
3V1+6(V1+7.5)=−45
3V1+6V1+45=−45
9V1+45=−45
9V1=−90⇒V1=−10m/s
Substituting back to find V2:
V2=−10+7.5=−2.5m/s
Step 5: Calculate Final Kinetic Energy
Now we can calculate the final kinetic energy (KE_final):
For particle 1:
KE1,final=12×3×(−10)2=12×3×100=150J
For particle 2:
KE2,final=12×6×(−2.5)2=12×6×6.25=18.75J
Thus, the total final kinetic energy is:
KEfinal=KE1,final+KE2,final=150+18.75=168.75J
Step 6: Calculate Loss of Kinetic Energy
The loss of kinetic energy is given by:
ΔKE=KEinitial−KEfinal=337.5−168.75=168.75J
Final Answer
The loss of kinetic energy during the collision is approximately:
ΔKE≈169J
The initial kinetic energy (KE_initial) of the two particles can be calculated using the formula:
KE=12mu2
where m is the mass and u is the initial velocity.
KE1=12×3×(5)2=12×3×25=37.5J
KE2=12×6×(10)2=12×6×100=300J
KEinitial=KE1+KE2=37.5+300=337.5J
The total momentum before and after the collision must be conserved. The initial momentum pinitial is given by:
pinitial=m1u1+m2(−u2)=3×5+6×(−10)=15−60=−45kg m/s
pfinal=m1V1+m2V2
Setting pinitial=pfinal:
3V1+6V2=−45(Equation 1)
The coefficient of restitution e relates the velocities before and after the collision:
e=V2−V1u1+u2
Given e=0.5, u1=5, and u2=10:
0.5=V2−V15+10=V2−V115
Thus,
V2−V1=0.5×15=7.5(Equation 2)
Now we have two equations:
1. 3V1+6V2=−45
2. V2−V1=7.5
V2=V1+7.5
Substituting into Equation 1:
3V1+6(V1+7.5)=−45
3V1+6V1+45=−45
9V1+45=−45
9V1=−90⇒V1=−10m/s
Substituting back to find V2:
V2=−10+7.5=−2.5m/s
Now we can calculate the final kinetic energy (KE_final):
For particle 1:
KE1,final=12×3×(−10)2=12×3×100=150J
For particle 2:
KE2,final=12×6×(−2.5)2=12×6×6.25=18.75J
KEfinal=KE1,final+KE2,final=150+18.75=168.75J
The loss of kinetic energy is given by:
ΔKE=KEinitial−KEfinal=337.5−168.75=168.75J
The loss of kinetic energy during the collision is approximately:
ΔKE≈169J
Similar Questions
Two particles of masses m1=6kg&m2=4kg move towards each other with u1=3m/sec&u2=6m/sec respectively. If they collide elastically, find the impulse of the particles.
View SolutionTwo identical balls each of mass 4 kg are moving towards each other with speeds 2 m/s and 3 m/s respectively. They undergo head on perfectly elastic collision. Then impulse imparted by one ball on other is
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then
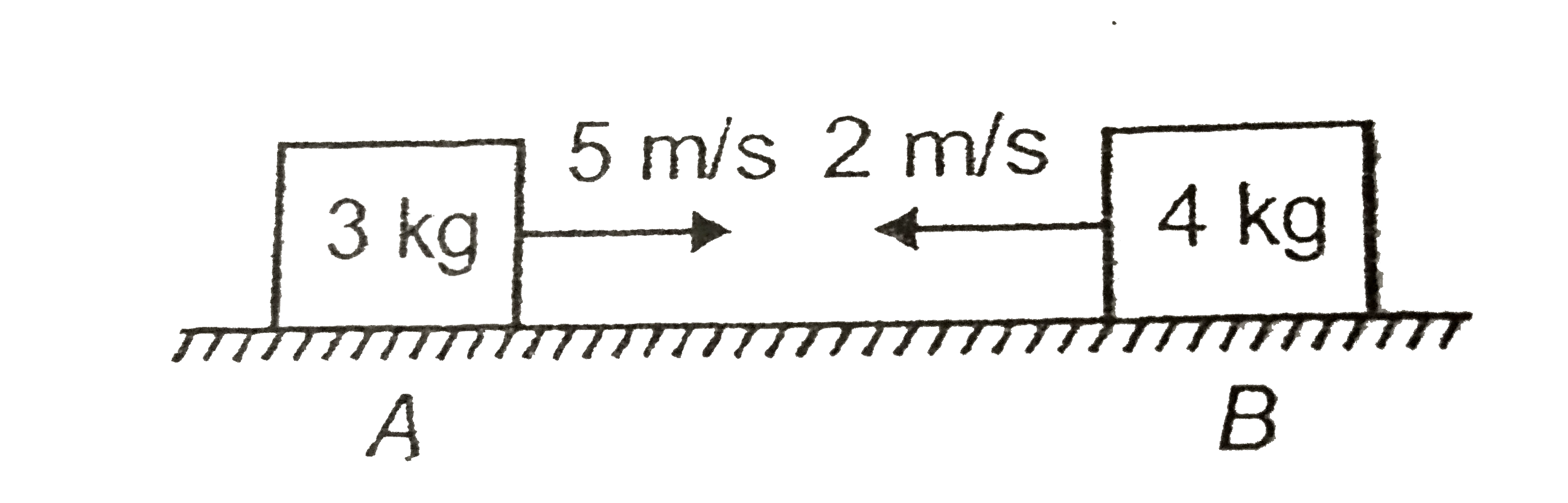
Velocity of A after collision
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then

Velocity of B after collision
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then

Loss in kinetic energy in collision
View SolutionTwo particles A and B of equal size but of masses mkg and 2mkg are moving directly towards each other with speeds 21m/s and 4m/s respectively. After collision, A moves with a speed of 1m/s in the original direction. Then:
View SolutionTwo particles of mass 1kg and 2kg are moving along the same line with speeds 2m/s and 4m/s respectively. Calculate the speed of the centre of mass of the system if both the particles are moving in the same direction.
View SolutionTwo particles of mass 1kg and 2kg are moving along the same line with speeds 2m/s and 4m/s respectively. Calculate the speed of the centre of mass of the system if both the particles are moving in the same direction.
View SolutionTwo particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
View SolutionTwo steel balls A and B of mass 10 kg and 10 g rolls towards each other with 5m/s and 1 m/s respectively on a smooth floor. After collision, with what speed B moves [perfectly elastic collision]?
View Solution
