Find the loss of KE of the two particles of mass m1=3kg&m2=6kg, moving towards each other with speed u1=5m/s,u2=10m/s respectively. The coefficient of restitution of collision of the particles is e = 0.5.
The correct Answer is:169 J
To find the loss of kinetic energy during the collision of two particles, we will follow these steps:
Step 1: Identify the given values
- Mass of particle 1, m1=3kg
- Mass of particle 2, m2=6kg
- Initial velocity of particle 1, u1=5m/s
- Initial velocity of particle 2, u2=10m/s
- Coefficient of restitution, e=0.5
Step 2: Calculate the initial kinetic energy (KE_initial)
The initial kinetic energy of the two particles can be calculated using the formula:
KEinitial=12m1u21+12m2u22
Substituting the values:
KEinitial=12×3×(5)2+12×6×(10)2
Calculating each term:
=12×3×25+12×6×100
=752+6002
=37.5+300=337.5J
Step 3: Apply the conservation of momentum
Using the conservation of momentum before and after the collision:
m1u1+m2(−u2)=m1v1+m2v2
Substituting the values:
3×5−6×10=3v1+6v2
15−60=3v1+6v2
−45=3v1+6v2(Equation 1)
Step 4: Use the coefficient of restitution
The coefficient of restitution is defined as:
e=v2−v1u1+u2
Substituting the known values:
0.5=v2−v15+10
0.5=v2−v115
Multiplying both sides by 15:
7.5=v2−v1(Equation 2)
Step 5: Solve the equations
From Equation 2:
v2=v1+7.5
Substituting v2 in Equation 1:
−45=3v1+6(v1+7.5)
Expanding:
−45=3v1+6v1+45
Combining like terms:
−45=9v1+45
Subtracting 45 from both sides:
−90=9v1
Dividing by 9:
v1=−10m/s
Now substituting back to find v2:
v2=−10+7.5=−2.5m/s
Step 6: Calculate the final kinetic energy (KE_final)
Now, we can calculate the final kinetic energy:
KEfinal=12m1v21+12m2v22
Substituting the values:
KEfinal=12×3×(−10)2+12×6×(−2.5)2
Calculating each term:
=12×3×100+12×6×6.25
=150+18.75=168.75J
Step 7: Calculate the loss of kinetic energy
The loss of kinetic energy is given by:
ΔKE=KEinitial−KEfinal
Substituting the values:
ΔKE=337.5−168.75=168.75J
Final Answer
The loss of kinetic energy during the collision is 168.75 J.
---
- Mass of particle 1, m1=3kg
- Mass of particle 2, m2=6kg
- Initial velocity of particle 1, u1=5m/s
- Initial velocity of particle 2, u2=10m/s
- Coefficient of restitution, e=0.5
The initial kinetic energy of the two particles can be calculated using the formula:
KEinitial=12m1u21+12m2u22
Substituting the values:
KEinitial=12×3×(5)2+12×6×(10)2
Calculating each term:
=12×3×25+12×6×100
=752+6002
=37.5+300=337.5J
Using the conservation of momentum before and after the collision:
m1u1+m2(−u2)=m1v1+m2v2
Substituting the values:
3×5−6×10=3v1+6v2
15−60=3v1+6v2
−45=3v1+6v2(Equation 1)
The coefficient of restitution is defined as:
e=v2−v1u1+u2
Substituting the known values:
0.5=v2−v15+10
0.5=v2−v115
Multiplying both sides by 15:
7.5=v2−v1(Equation 2)
From Equation 2:
v2=v1+7.5
Substituting v2 in Equation 1:
−45=3v1+6(v1+7.5)
Expanding:
−45=3v1+6v1+45
Combining like terms:
−45=9v1+45
Subtracting 45 from both sides:
−90=9v1
Dividing by 9:
v1=−10m/s
Now substituting back to find v2:
v2=−10+7.5=−2.5m/s
Now, we can calculate the final kinetic energy:
KEfinal=12m1v21+12m2v22
Substituting the values:
KEfinal=12×3×(−10)2+12×6×(−2.5)2
Calculating each term:
=12×3×100+12×6×6.25
=150+18.75=168.75J
The loss of kinetic energy is given by:
ΔKE=KEinitial−KEfinal
Substituting the values:
ΔKE=337.5−168.75=168.75J
The loss of kinetic energy during the collision is 168.75 J.
Topper's Solved these Questions
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I
45 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I (ASSERTION REASONING TYPE)
2 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Numerical)
8 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
Similar Questions
Two particles of masses m1=6kg&m2=4kg move towards each other with u1=3m/sec&u2=6m/sec respectively. If they collide elastically, find the impulse of the particles.
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then

Loss in kinetic energy in collision
View Solution
Knowledge Check
Two particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
A103m/sB107m/sC112m/sD123m/sTwo balls of masses 2m and m are moving with speed 2v0 and v0 towards each other. If the coefficient of restitution e=1/3 , the speed of balls , if collision is head - on
Av03,4v03B2v03,5v03C2v03,4v03Dv03,2v03A particle of mass m1 collides head on with a stationary particles of mass m2. If m1m2 gte, where e is the coefficient of restitution, then :
Am1 will retrun backBm1 will move in same directionCm1 will stopDunpredictable
Two particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then

Velocity of B after collision
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then
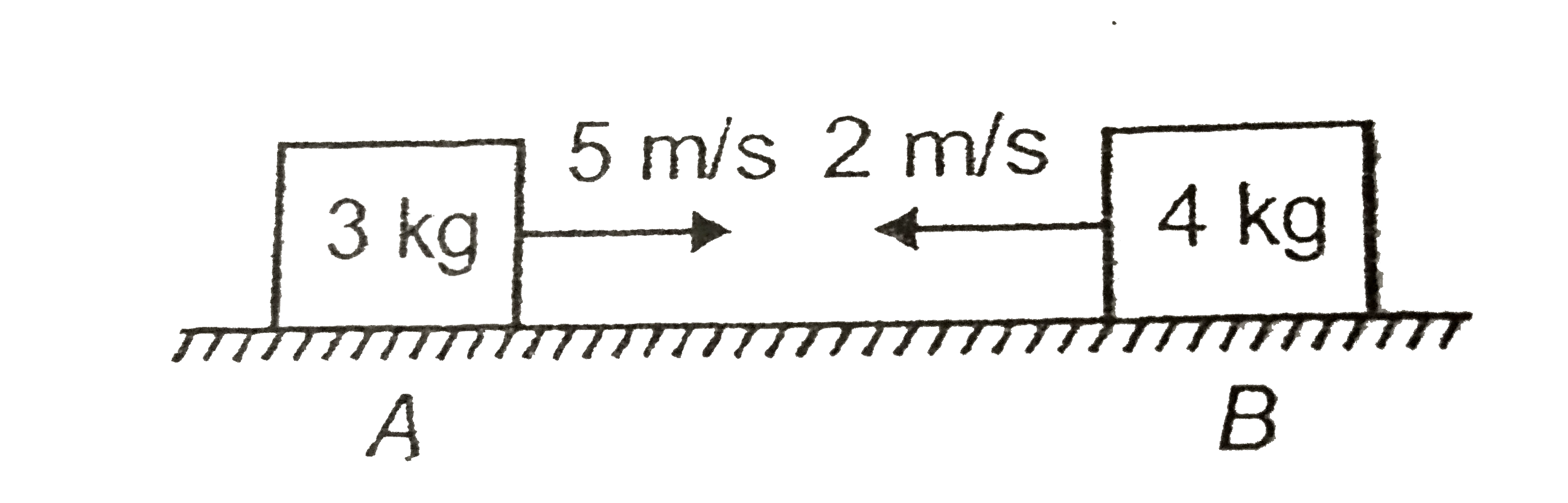
Velocity of A after collision
View SolutionTwo particles of mass 1kg and 2kg are moving along the same line with speeds 2m/s and 4m/s respectively. Calculate the speed of the centre of mass of the system if both the particles are moving in the same direction.
View SolutionTwo particles A and B of equal size but of masses m kg and 2 m kg are moving directly towards each other with speeds 21 m/s and 4 m/s respectively. After collision, A moves with a speed of 1 m/s in the original direction. Then:
View SolutionTwo bodies of masses 0.1 kg and 0.4 kg move towards each other with the velocities 1 m/s and 0.1 m/s respectively, After collision they stick together. In 10 sec the combined mass travels
View Solution
