Figure 22-8e is identical to Fig 22-8a except that particle 4 is now included. It has charge q4=−3.20×10−19C, is at a distance 34 R from particle 1, and lies on a line that makes an angle θ=60∘ with the x axis. What is the net electrostatic electrostatic electrostatic force →F1, net on particle 1 due to particle 2 and 4?
KEY IDEAS
The net force →F1, net is the vector sum of →F1, net and a new force →F14 acting on particle 1 due to particle 4. Because particles 1 and 4 have charge of opposite signs, particle 1 is attracted to particle 4. Thus, force →F14 on particle 1 is directed toward particle 4, at angle θ=60∘, as indicated in the free-body diagram of Fig. 22-8f.
Four particles: We can rewrite Eq.22−4 as
F14=14πε0|q1||q4|(34R)2
=(8.99×109N⋅m2/C2)×(1.60×10−19C)(3.20×10−19C)(34)2(0.0200m)2
=2.05×10−24N.
Then from Eq. 22-7, we can write the net force on →F1.net particle 1 as
→F1, net=→F12+→F14.
Because the forces →F12and→F14 are not directed along the same axis, we cannot sum simply by combining their magnitudes. Instead, we must add them as vectors, using one of the following methods.
Method 1. summing directly on a vector-capable calculator. For →F12, we enter the magnitude 1.15×10−24 and the angle 180∘ For →F14, we enter the magnitude 2.05×10−24 and the angle 60∘. Then we add the vectors.
Method 2. Summing in unit-vector notation. First we rewrite →F14 as
→F14=(F14cosθ)ˆi+(F14sinθ)ˆj.
Substituting 2.05×10−24N for F14and60∘ for θ, this becomes
→F14=(1.025×10−24N)ˆi+(1.775×10−24N)ˆj.
Then we sum:
→F1, net=→F12+→F14
=−(1.15×10−24N)ˆi+(1.025×10−24N)ˆi+(1.775×10−24N)ˆj
=(−1.25×10−25N)ˆi+(1.78×10−24N)ˆj. (Answer)
Method 3. Summing components axis by axis. The sum of the x components gives us
F1, net, x=F12,x+F14,x=F12+F14cos60∘
=−1.15×10−24N+(2.05×10−24N)(cos60∘)
=−1.25×10−25N.
The sum of the y components gives us
F1, net, y=F12,y+F14,y=0+F14sin60∘
=(2.05×10−24N)(sin60∘)
=1.78×10−24N.
The net force →F1, net has the magnitude
F1, net=√F21, net, x+F21, net, y=1.78×10−24N. (Answer)
To find the direction of →F1, net, we take
θ=tan−1F1, net,yF1,net,x=−86.0∘.
However, this is an unreasonable result because →F1,net must have a direction between the directions of →F12 and →F14. To correct θ, we add 180∘, obtaining
=86.0∘+180∘=94.0∘ (Answer)
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points9videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Problems63videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELASTICITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type1videos
ELECTRIC POTENTIAL
Similar Questions
Figure 22-8c is identical to Fig. 22-8a except that particle 3 now lies on the x axis between particles 1 and 2. Particle 3 has charge q2=−3.20×10−19C and is at a distance (3/4)R from particle 1. What is the net electrostatic force →F1.net on particle 1 due to particles 2 and 3?
View SolutionFigure shows an arrangement of four charged particles, with angle θ=35.0∘ and distance d = 2.00 cm. Particle 2 has charge q2=+8.00×10−19C, particle 3 and 4 have charges q3=q4=−1.60×10−19C, (a) What is distance D between the origin and particle 2 if the net electrostatic force on particle 1 due to the other particles is zero ? (b) If particles 3 and 4 were moved closer to the x axis but maintained their symmetry about that axis, would the required value of D be greater than, less than, or the same as the part (a) ?
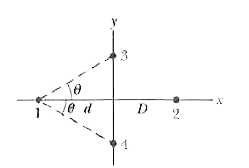View SolutionTwo positively charged particles fixed in place on an x axis. The charges are q1=1.60×10−19Candq2=3.20×10−19C, and the particle separation is R = 0.0200m. What are teh magnitude and direction of the electrostatic force →F12 on particle 1 from particle 2?
View SolutionIn fig. a central particle of charge −q is surrounded by two circular rings of charged particle of radii r and R, with Rgtr. what is the magnitude and dirction of the net electrostatic force on the central particle due to the other particles?
View SolutionIn fig. a central particle of charge −q is surrounded by two circular rings of charged particle of radii r and R, with Rgtr. what is the magnitude and dirction of the net electrostatic force on the central particle due to the other particles?
View SolutionTwo charged particles are attached to an x axis: Particle 1 of charge −4.00×10−7C is at position x = -5.00 cm and particle 2 of charge +4.00×10−7C is at position x = 10.cm. Midway between the particles, what is their net electric field in unit-vector notation ?
View SolutionFigure 22-18a shows there particles with charges q1=+2Q,q2=−2Q,andq3=−2Q, each a distance d from the origin. What net electric field →E is produced at the origin?
View SolutionIn Fig., particles 1 and 2 have charge 20.0μC each and are held at separation distance d = 0.75 m. (a) What is the magnitude of the electrostatic force on particle 1 due to particle 2? In Fig., particle 3 of charge 20.0μC is positioned so as to complete an equilateral triangle. (b) What is the magnitude of the net electrostatic force on particle 1 due to particles 2 and 3 ?
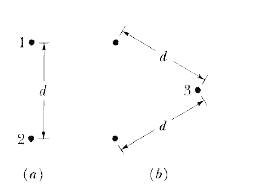View SolutionIn Fig., particles 1 and 2 are fixed in place on an axis, at a separation of L = 6.00 cm. Their charges are q1=+e and q2=−27e. Particle 3 with charge q3=+4e is to be placed on the line between particles 1 and 2 , so that they produce a net electrostatic force →F3,net on it. (a) At what coordinate should particle 3 be placed to minimize the magnitude of that force ? (b) What is that minimum magnitude ?
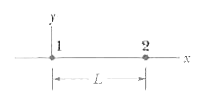View SolutionIn Fig. 22-19, particle 1 of charge q1=5.00q and a particle 2 of charge q2+2.00q are fixed on the x-axis.
As a multiple of distance L, at what coordinate on the axis is the net electric field of the particles zero?
View Solution