Figure here shown P and Q as two equally intense coherent sources emitting radiations of wavelength 20 m. The separation PQ is 5.0 m and phase of Q is ahead of the phase of P by 90∘. A,B and C are three distant points of observation equidistant from the mid-point of PQ. The intensity of radiations at A,B and C will bear the ratio
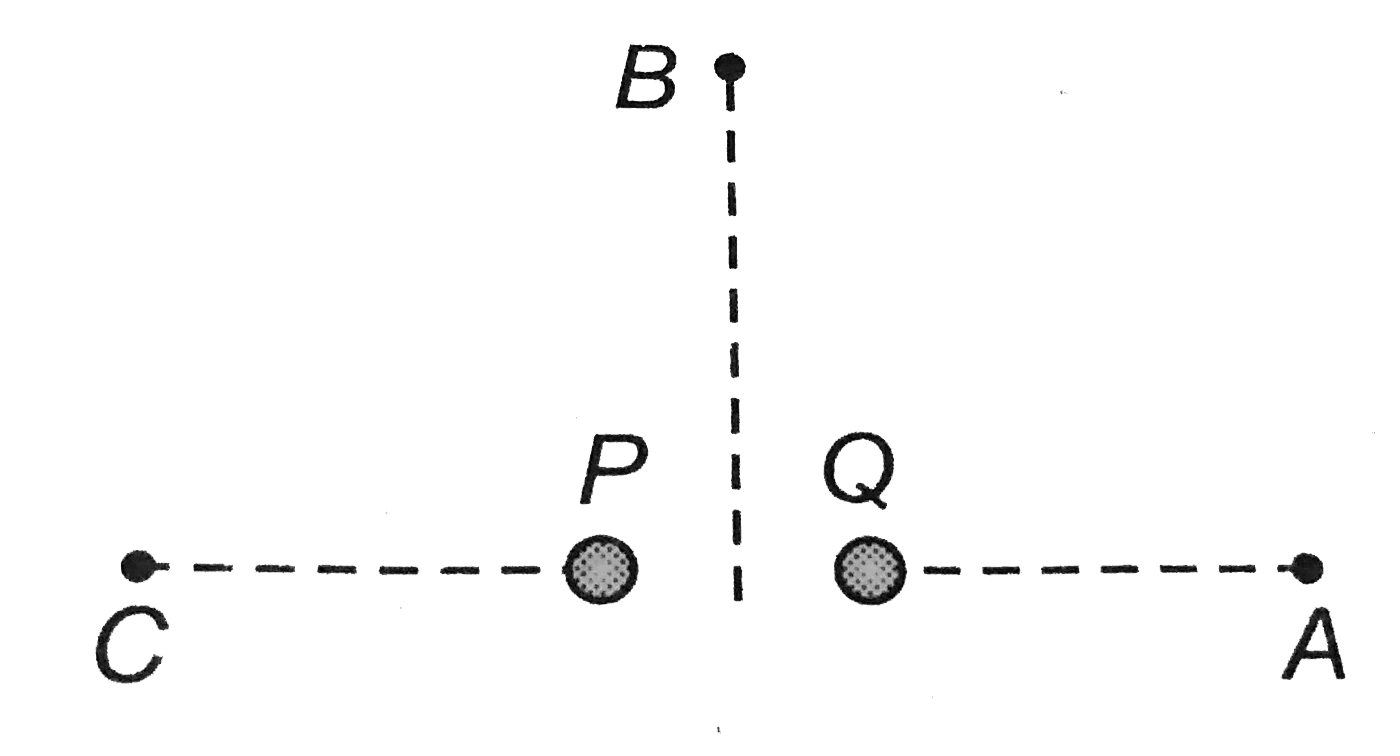
0:1:4
4:1:0
0:1:2
2:1:0
The correct Answer is:D
Step by step video, text & image solution for Figure here shown P and Q as two equally intense coherent sources emitting radiations of wavelength 20 m. The separation PQ is 5.0 m and phase of Q is ahead of the phase of P by 90^(@). A,B and C are three distant points of observation equidistant from the mid-point of PQ. The intensity of radiations at A,B and C will bear the ratio by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Fig, here shows P and Q as two equally intense coherent sources emitting radiations of wavelength 20m. The separation PQ si 5m, and phase of P is ahead of the phase Q by 90∘. A, B and C are three distant points ofobservation equidistant from the mid - point of PQ. The intensity of radiations of A, B, C will beasr the ratio
 A0:1:4B4:1:0C0:1:2D2:1:0
A0:1:4B4:1:0C0:1:2D2:1:0P and Q are points on the line joining A(-2,5) and B(3,1) such that AP=PQ=QB. Then the mid pont of PQ is
A(12,3)B(−12,4)C(2,3)D(1,4)Two waves are propagating to the point P along a straight line produced by two sources A and B of simple harmonic and of equal frequency. The amplitude of every wave at P is a and the phase of A is ahead by π/3 than that of B and the distance AP is greater than BP by 50cm. Then the resultant amplitude at the point P will be if the wavelength is 1 meter
A2aBa√3Ca√2Da
If the point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), find p.
View SolutionIf A=(1,2,3) and B(3,5,7) and P,Q are the points on AB such that AP=PQ=QB, then the mid point of PQ is
View SolutionA point source of constant power P is emitting photon of wavelength λ. What is the intensity of photons at r distance from the source ?(speed of light = c)
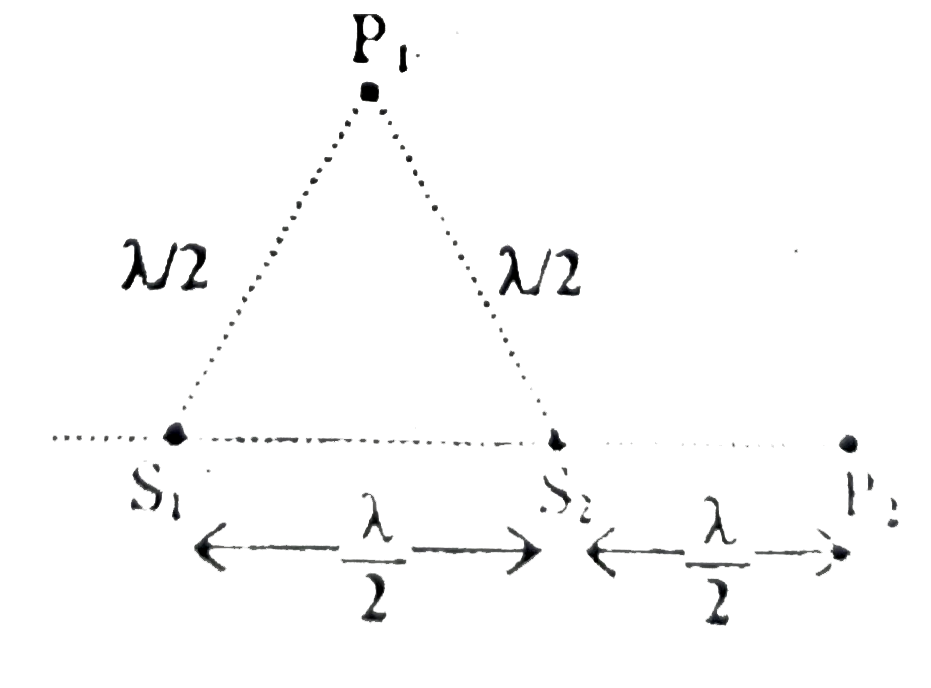
View SolutionS1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
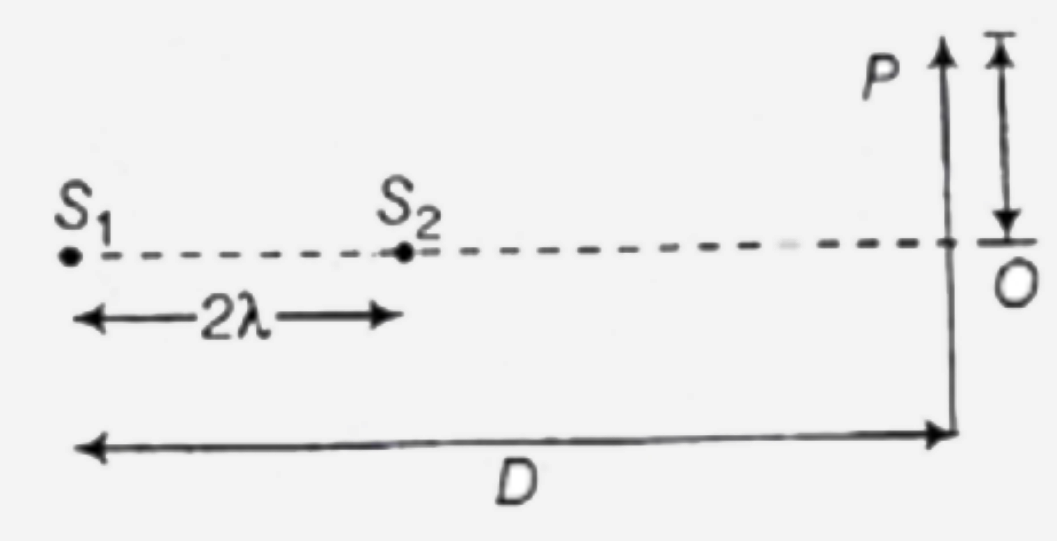
View SolutionTwo coherent point sources S1andS2 vibrating in phase emit light of wavelength λ . The separation between them is 2λ . The light is collected on a screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O
View Solution
