Figure shows a block A of mass 6m having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block B of mass m is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
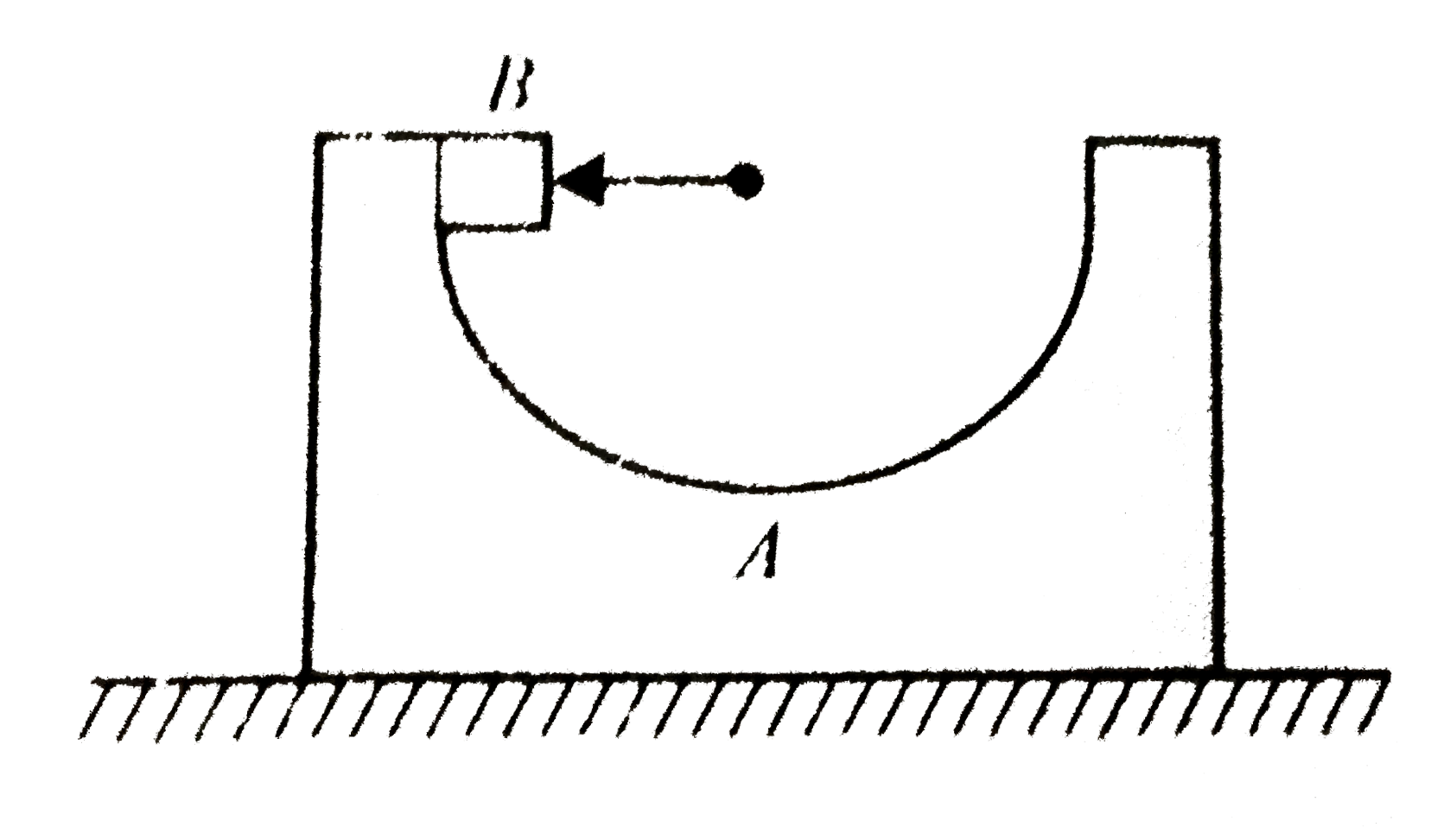
Let the smaller block is moving with speed v1 relative to the bigger block when it reaches the bottommost position and at this instant bigger block is moving at v2 (say). Then using conservation of momentum in horizontal direction, we have
6mv2=m(v1−v2) .........i
Now using energy conservation
mga=12m(v1−v2)2+12(6m)v21
...........ii
solving eqn i and ii we get
2ga−36v22+6v22
v2=√ga21
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
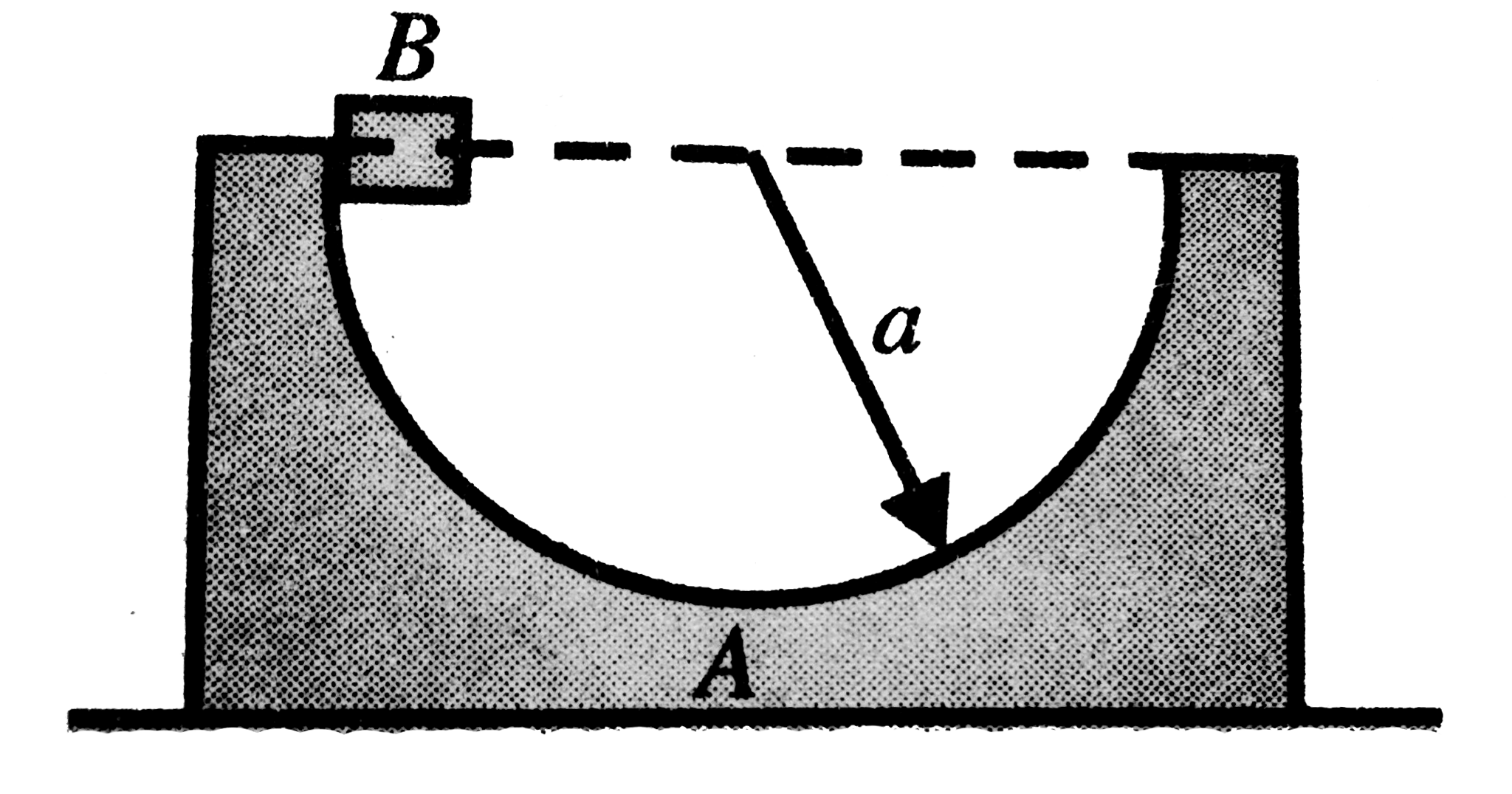
Figure shows a wedge A of mass 6m smooth semicircular groove of radius a=8.4m placed on a smooth horizontal surface. A small block B of mass m is released from a position in groove where its radius is horizontal. Find the speed (in ms−1) of bigger block when smaller block reaches its bottommost position.
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View Solution
Knowledge Check
The figure shows a block of mass M=2m having a spherical smooth cavity of radius R placed on a smooth horizontal surface .There is a small ball of mass m moving at an instant vertically downward with a velocity v with respect to the block .At this instant :
 AThe normal reaction on the ball by the block is mv2RBThe normal reaction on the ball by the block is 23mv2RCThe acceleration of the block with respect to the ground is v23RDThe acceleration of the block with respect to the ground is v22R
AThe normal reaction on the ball by the block is mv2RBThe normal reaction on the ball by the block is 23mv2RCThe acceleration of the block with respect to the ground is v23RDThe acceleration of the block with respect to the ground is v22RA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.
 AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at B
AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at B
Figure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mas m placed on a horizontal floor. The curved part of the surface shown is semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.

View SolutionA smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?

View Solution
A block is released from position A in the following figure. Find the speed of the block in position B. Assume the surface as frictionless.
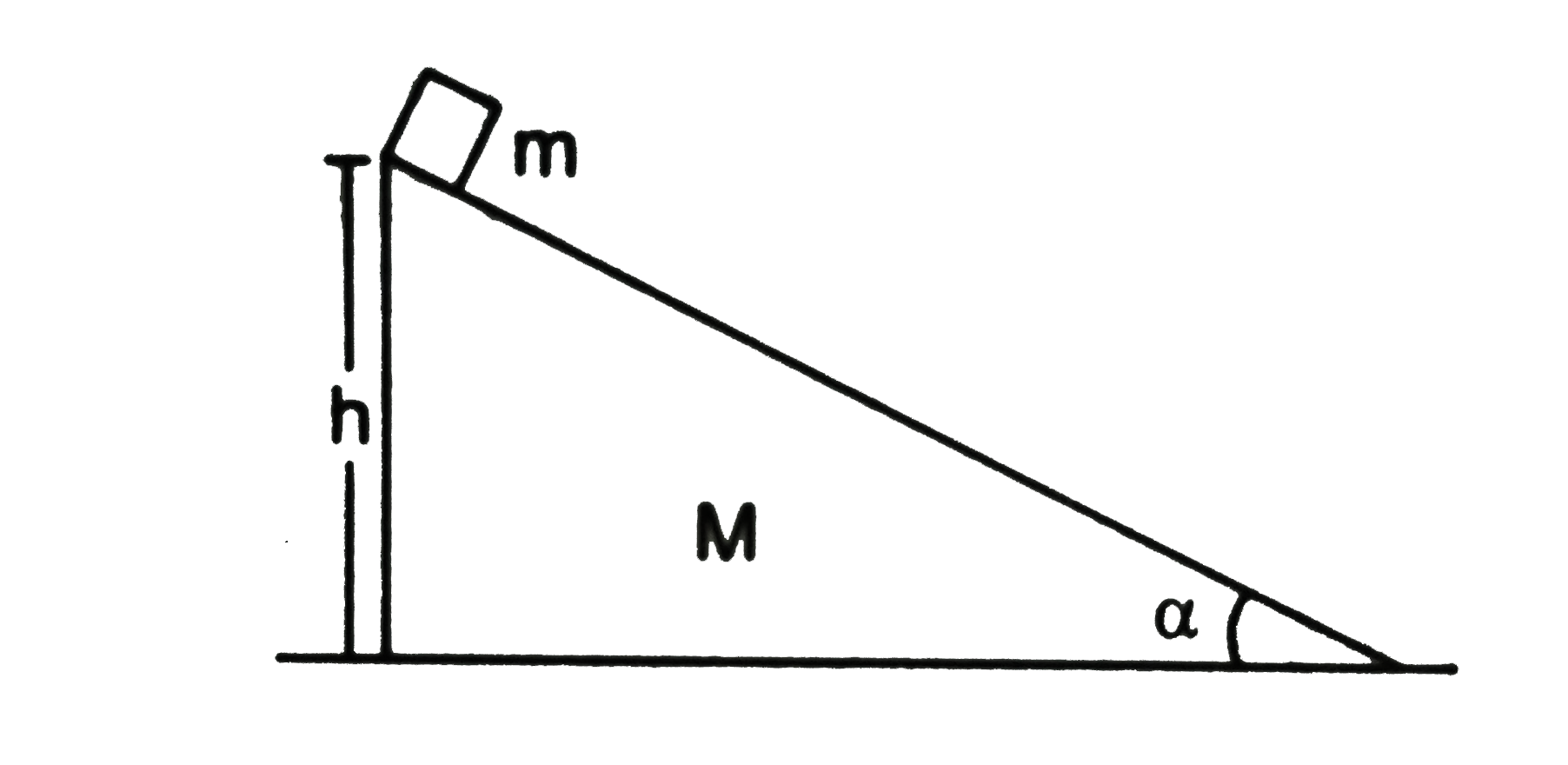
View SolutionA block of mas m is placed on a triangular block of mas m, which in tunis placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
View SolutionA block of mass m is placed on a triangular block of mass M(M=2m) , as shown. All surfaces are smooth. Calculate the velocity of triangular block when the smaller block reaches at bottom.

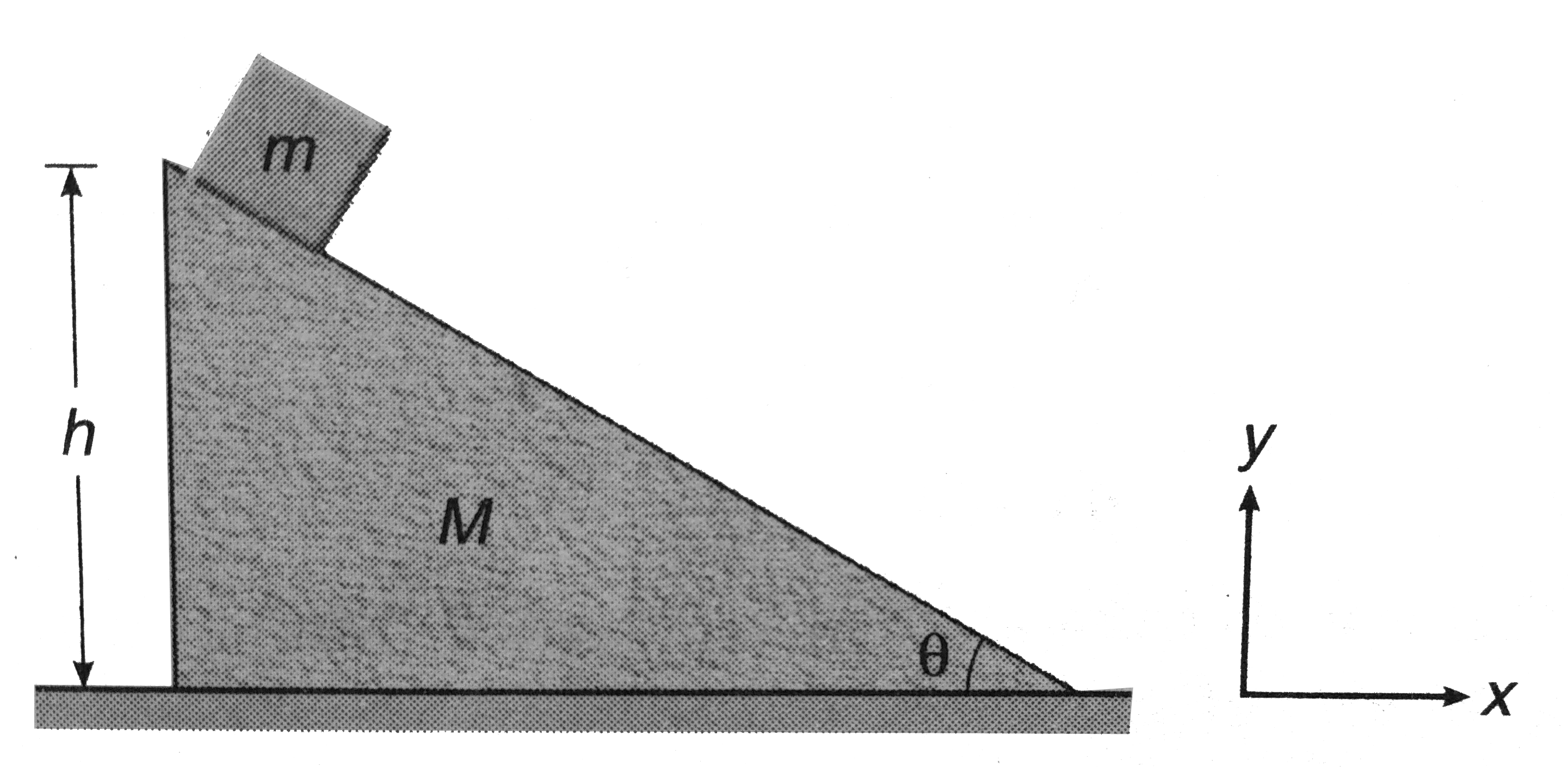
View SolutionA block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
View Solution
