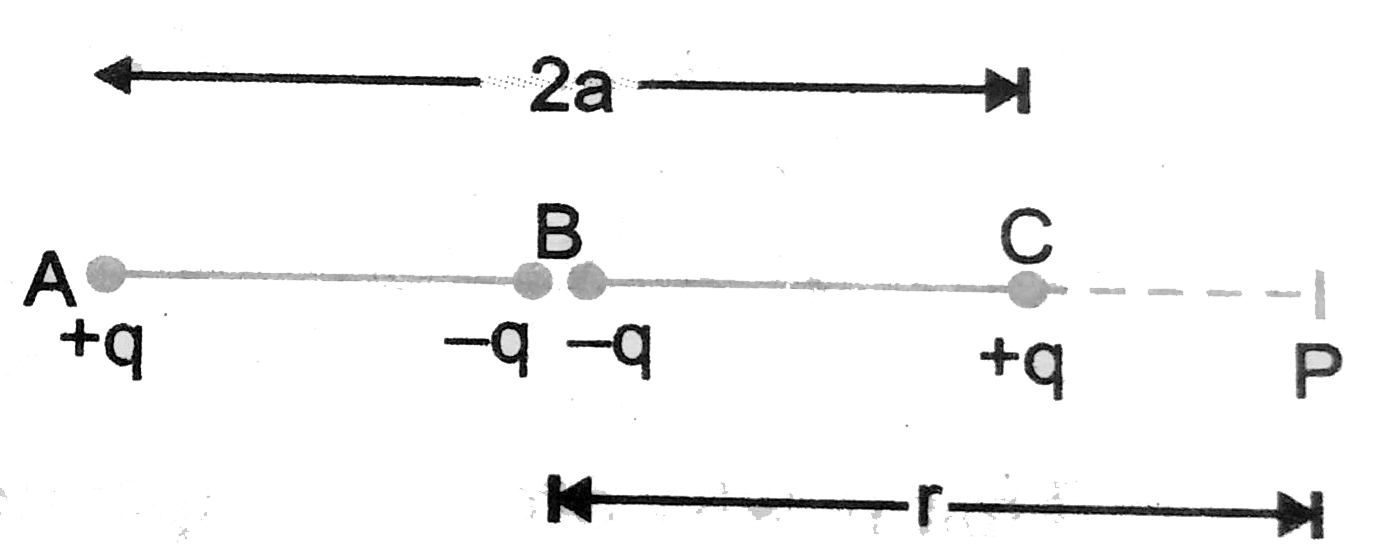
Figure shows a charge array known as an 'electric quadrupole'. For a point on the axis of the quadrupole, obtain the dependence of potential on r for ra>>1, and contrast your results with that due to an electric dipole, and an electric monopole (i.e., a single charge).

For the electric quadrupole shown in the above figure, net electric potential at point P is
V=14πε0[q(r+a)−2qr+q(r−a)]=q4πε0[1r+a+1r−a−2r]
=q4πε0[r(r−a)+r(r+a)−2(r2−a2)r(r2−a2)]=q4πε0.2a2r(r2−a2)
=q.2a24πε0r3(1−a2r2)=2qa24πε0r3(1−a2r2)
Forra>>1i.e.,ar>>1 we have : V=2qa24πε0r3
Thus, V∝1r3 i.e., electric potential due to a quadrupole is inversely proportional to the cube of the distance along its axis. However, for a dipole V∝1r2 and for a monopole V∝1r.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS
18 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - MULTIPLE CHOICE QUESTIONS
35 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST
1 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Videos
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
Fig shows a charge array known as an 'electric quadrupole'. For a point on the axis of the quadrupole, obtain the dependence of potential on r for r/a>>1, and contract your results with that due to an electric dipole and an electric monopole (i.e, a single charge).
View SolutionFig shows a charge array known as an 'electric quadrupole'. For a point on the axis of the quadrupole, obtain the dependence of potential on r for r/a>>1, and contract your results with that due to an electric dipole and an electric monopole (i.e, a single charge).

View Solution
Knowledge Check
The electric potential V at a point on the axis of an electric dipole depends on the distance 'r of the point from the dipole as
AV∝1rBV∝1r2CV∝1r3DV∝rThe electric potential at a point on the axis of an electric dipole depends on the distance r of the point from the dipole as
A∝1rB∝1r2C∝rD∝1r3Electric potential (ϕ) of a quadrupole varies with distance 'r' on its axis as :-
Aϕ∞r−1Bϕ∞r−2Cϕ∞r−3Dϕ∞r−3/2
The figure given below shows a charge array known as an 'electric quadrupole'. For a point on the axis of the quadrupole, obtain the dependence of potential on r for ra>>1. Contrast your result with that due to an electric dipole and an electric monopole (i.e. a single charge).

View SolutionFigure shows a charge array known as an "electric quadrupole". For a point on the axis of the quadruple, the dependence of potential on r(ra>>1) is 1rn. Find n?
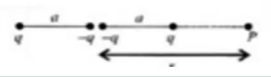
View SolutionFigure shows a charge array known as an "electric quadrupole". For a point on the axis of the quadruple, the dependence of potential on r(ra>>1) is 1rn. Find n?

View SolutionDeduce an expression for the electric potential due to an electric dipole at any point on its axis. Mention one contrasting feature of electric potential of a dipole at a point as compared to that due to a single charge.
View SolutionDeduce an expression for the electric potential due to an electric dipole at any point on its axis. Mention one contrasting feature of electric potential at a point due to dipole as compared to that due to a single charge.
View Solution
