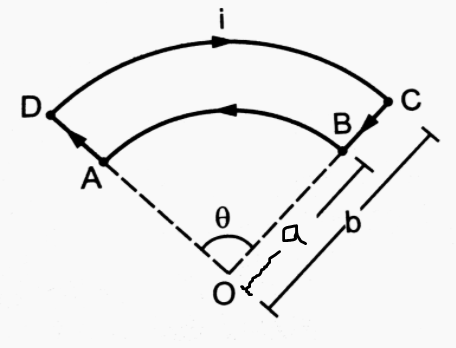
Figure shows a current loop having two circular arcs joined by two radial lines. Find the magnetic field B at the centre O.
 Solution in Tamil
Solution in Tamil
Solution: As the point O is on the line AD, the magnetic
field at O due to AD is zero. Similarly , the field at O
due to BC is also zero. The field at the centre of a
∘a––rcurrentl∞pisgivenbyB=((μ0)i2a).Thefielddue<br>→the∘a––rarcBAwillbe<br> B_1=(theta/ 2pi)((mu_0)i/2a)<br>Theright−handthumbre–showstˆthefieldis<br>comingoutofthepla≠ofthefigure.Thefielddue→<br>the∘a––rarcDCis<br> B_2= (theta/2 pi)((mu_0)i/2b) <br> going into the plane of the figure. The resultant field at
O is
B= ((B_1)-(B_2))= ((mu_0)i theta(b-a)/4 pi ab)
coming out of the plane.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 1
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - exercise
61 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
60 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercise
9 Videos
Similar Questions
An electric current flows in a wire from north to south.
What will be the direction of the magnetic field due to this wire at a point.
View SolutionA vertical wire carries a current in upward direction. An electron beam sent horizontally towards the wire will be deflected
View SolutionUsing the formulae ((→F)=(→qv)×(→B)andB=(μ0)i2πr,find the SI units of the magnetic field B and the permeability constant
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View SolutionThe magnetic intensity H at the centre of a long solenoid carrying a current of 2.0A, is found to be 1500Am−1. Find the number of turns per centimetre of the solenoid.
View SolutionFigure shows a current loop having two circular arcs joined by two lines. Find the magnitude field B at the centre O .
View SolutionThere is a uniform magnetic field (B) perpendicular to the plane of the figure in a circular region of radius a centred at O. ABCD is a conducing loop in the plane of the figure with its arms BC and DA along two radial lines from O having an angle θ between them. AB is circular arc of radius OB = d centred at O. CD is also a circular arc of radius OC=b centred at O. The magnetic field is changed at a rate dBdt.
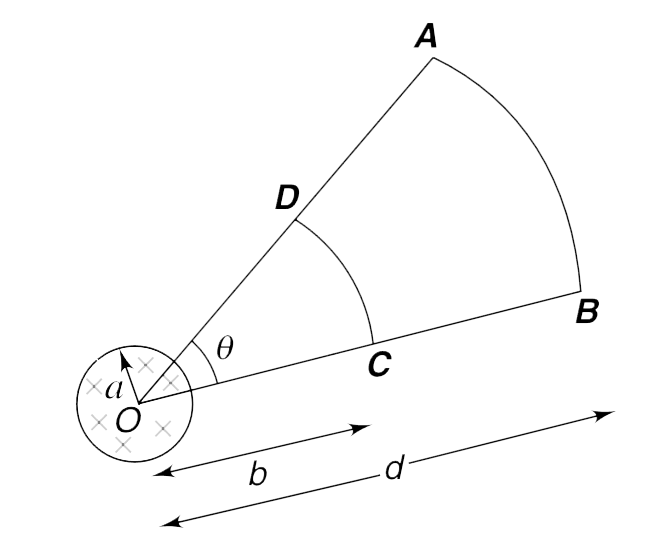
(a) The emf induced in the loop ABCD.
(b) Find emf induced in arc AB.
View SolutionIn the figure-4.30 shown two circular arcs are joined to make a closed loop carrying current l . Frnd the magnetic induction at the common centre 0.
View SolutionA current loop, having two circular arcs jo ined by two radial lines is shown in the figure. It carries a current of 10 A. The magnetic field at point O will be close to :
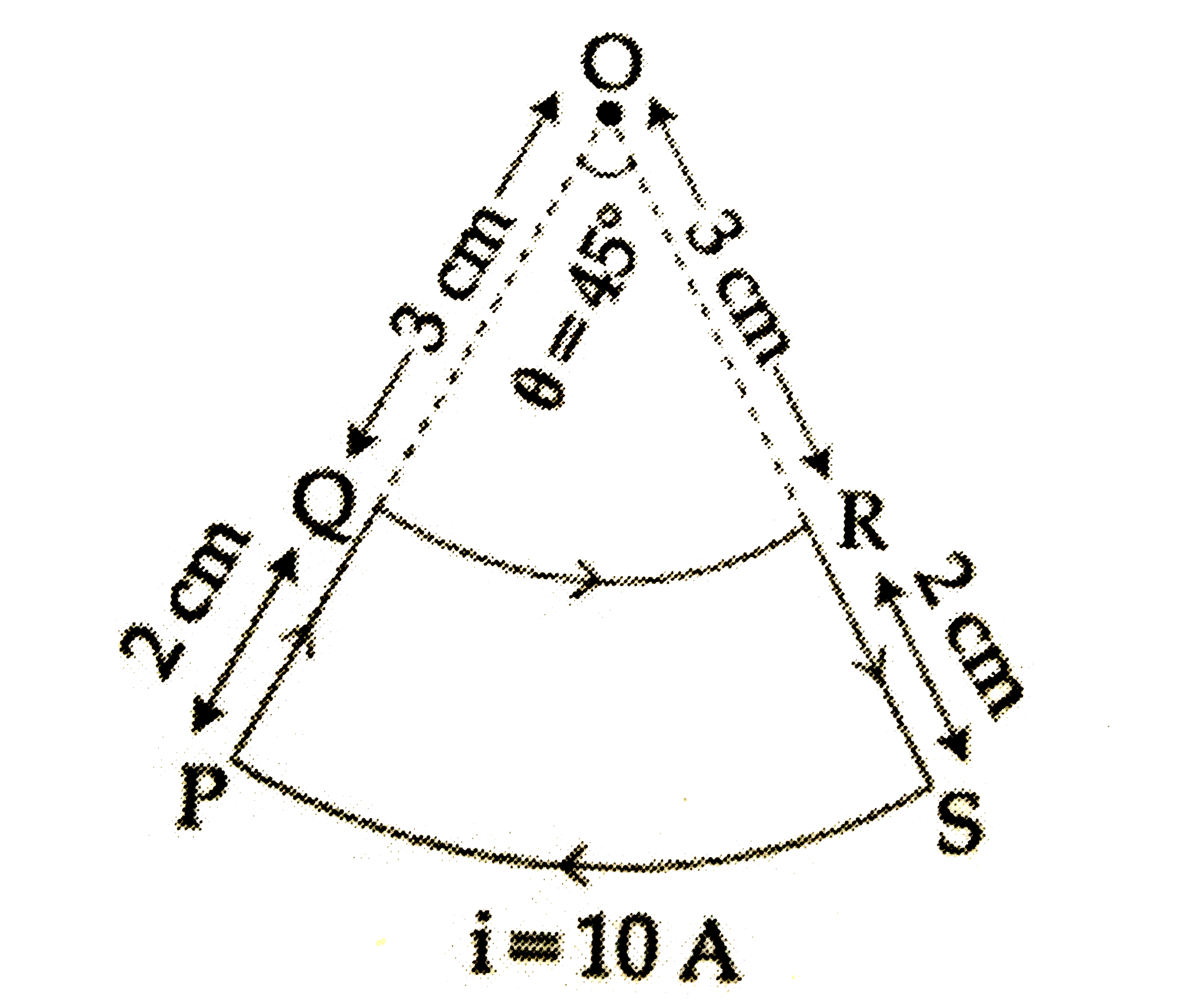
View SolutionA current loop, having two circular arcs jo ined by two radial lines is shown in the figure. It carries a current of 10 A. The magnetic field at point O will be close to :
View SolutionA loop ABCD has current I = 10 A , as shown in the figure . AD and BC are circular arcs with centre at O, for both . The magnetic field at point O is
View SolutionFind the magnetic field at the centre of the circular loop shown in figure.

View SolutionIn the following figure a current loop is shown which is made from two circular arcs of radii a and b(a<b), connected by radial wires. Calculate the magnetic field at the centre O.

View SolutionMagnetic field at the centre of a circular loop & arc
View SolutionShow magnetic field lines for current carrying loop. Write rule for finding the direction of a magnetic field due to a circular current loop.
View SolutionA current loop, having two circular arcs jo ined by two radial lines is shown in the figure. It carries a current of 10 A. The magnetic field at point O will be close to :
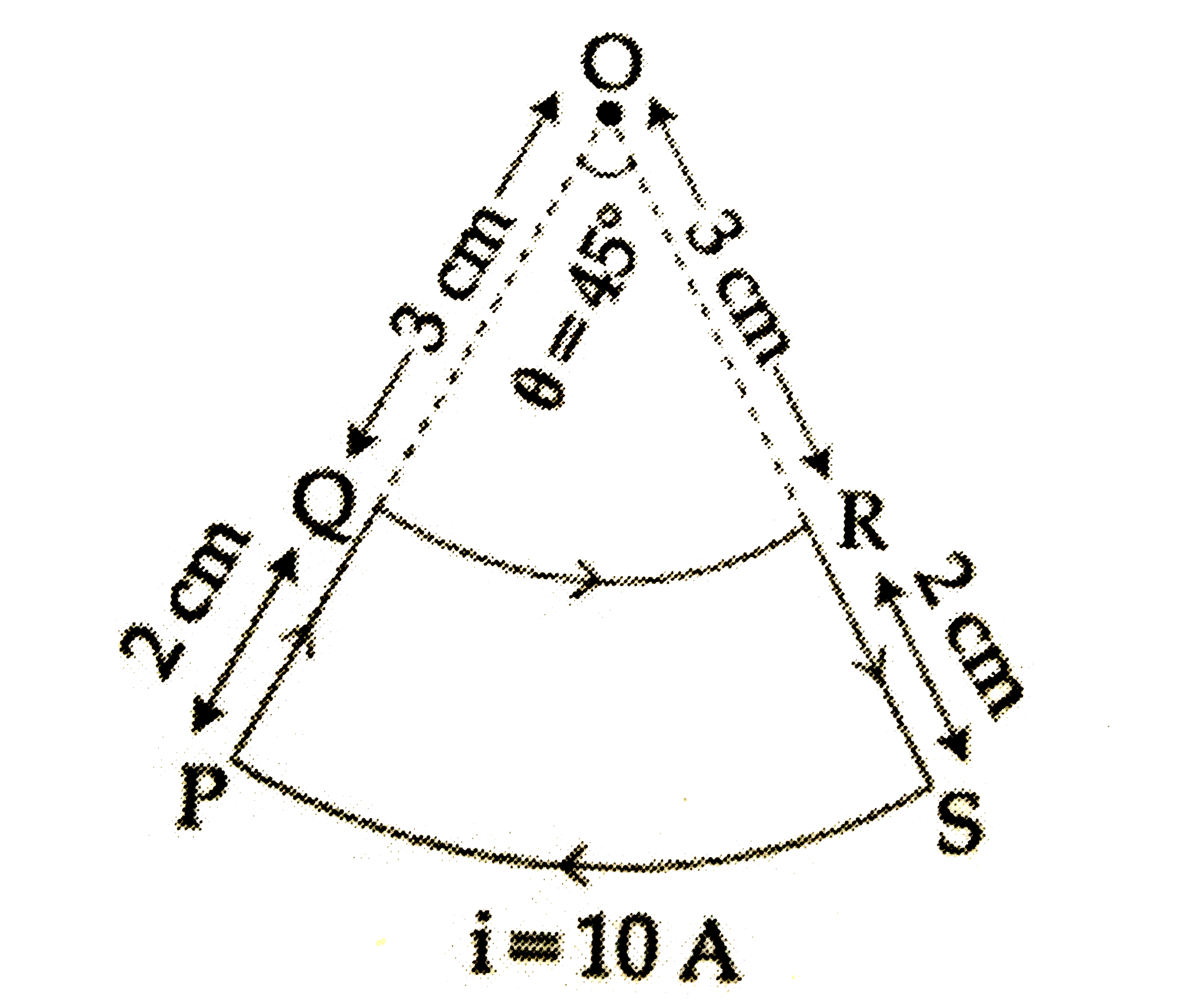
View Solution
