Question

Consider a coaxial cable which consists of an inner wire of radius a surrounded by an outer shell of inner and outer radii b and c respectively. The inner wire carries an electric current (i_0) and the outer shell carries an equal current in opposite direction. Find the magnetic field at a distance x from the axis where b.

Explanation

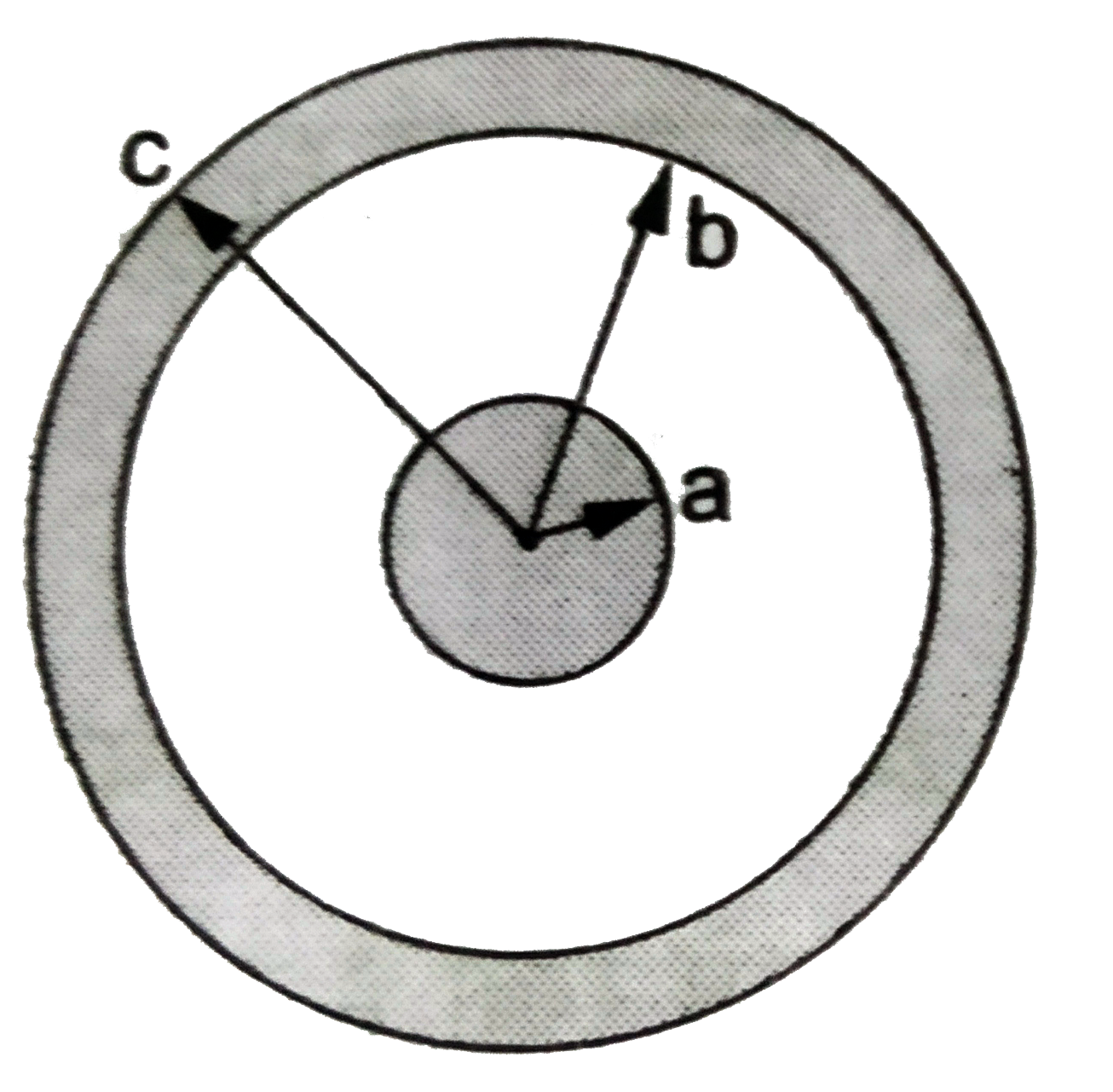
Solution: A cross section of the cable is shown in figure.
Draw a circle of radius x with the centre at the axis of
the cable. The parts a,b,c and d of the figure
correspond to the four parts of the problem.By
symmetry, the magnetic field at each point of a circle
will have the same magnitude and will be tangential to
it. The circulation of B along this circle is, therefore,
` oint (vec B). vec dl = B 2 pi x `
in each of the four parts of the figure.
` (a) The current enclosed within the circle in part a is `
` (i_0)/((pi a)^2). pi x^2 = ((i_0/a^2)x^2).`
` Ampere's law oint (vec B). (vec dl)= (mu_0)i gives `
` B 2 pi x = ((m_0)(i_0)(x^3)/(a^2)) or B= (((mu_0)(i_0)x)/((2 pi a)^2))`
The area of cross section of the outer shell is
` pi c^2- pi b^2. The area of cross section of the outer shell`
` within the circle in part c of the figure is (pi x^2 - pi b^2). `
` Thus, the current through this part is ((i_0(x^2-b^2))/(c^2-b^2)). This is`
` in the opposite direction to the current (i_0) in the inner `
` wire. Thus, the net current enclosed by the circle is `
` (i_0)-((i_0(x^2-b^2))/(c^2-b^2))= ((i_0(c^2- x^2))/(c^2-b^2))` .
From Ampere's law,
` B 2pix= ((mu_0)(i_0)(c^2-x^2)/(c^2-b^2))`
` or, B= ((mu_0)(i_0)(c^2-x^2)/(2 pi x (c^2-b^2))).`
` (d) The net current enclosed by the circle in part d of `
the figure is zero and hence
` B 2pi x = 0 or, B=0.`