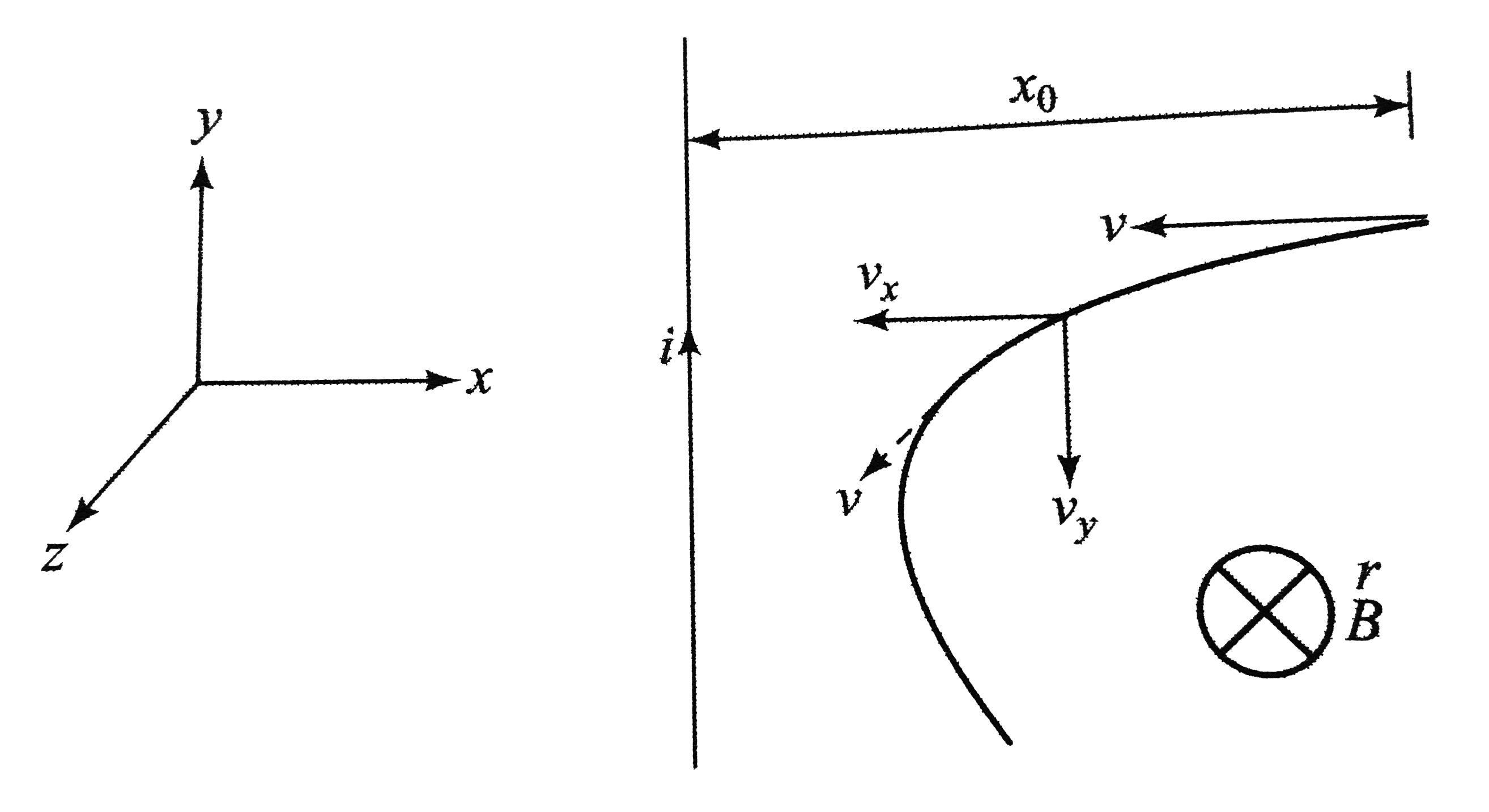
A long , straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance x_0 from the wire is projected towards it with a speed v. Find the minimum separation between the wire and the particle.
Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Solution: Let the particle be initially at P. Take
the wire as the y axis and the foot of perpendicular from
P to the wire as the origin. Take the line OP as the
$x - a ξ s . W e h a v e, O P = x_{0} . T h e m a g \neq t i c f i e l d B a t a n y < b r > p \oint \to t h e r i g h t o f t h e w i r e i s a l o n g t h e \neg a t i v e z - a ξ s . < b r > T h e m a g \neq t i c f or c e o n t h e p a r t i c \leq i s, ∴, \in t h e < b r > x - y p l a \neq . A s t h e r e i s n o \in i t i a l v e l o c i t y a l o n g t h e z - a ξ s, < b r > t h e m o t i o n w i l l b e \in t h e x - y p l a \neq . A l s o, i t s s p e e d < b r > r e m a \in s u n c h a n \geq d . A s t h e m a g \neq t i c f i e l d i s \neg < b r > u n if or m, t h e p a r t i c \leq d o e s \neg g o a l o n g a \circ \leq . < b r > T h e f or c e a t t i m e t i s$ ( vec F)= (vec qv) xx (vec B) $< b r >$ = q((vec i)vx + (vec j)vy) xx (- (mu_0)i/2 pi x) vec k) $< b r >$ = ((vec j) q(v_x)) ((mu_0)i/2pi x) - (( vec i ) (qv_y)((mu_0)i/2 pi x) $< b r > T h u s a_{x} = (\frac{F_{x}}{m}) = - ((μ_{0}) q \frac{i}{2} π m) (\frac{v_{y}}{x}) = - λ (\frac{V_{y}}{x}) ... ... . (i)$
$w h e r e λ = ((μ_{0}) q \frac{i}{2} π m) .$
$A l s o, a_{x} = (\frac{d v_{x}}{d t}) = (d \frac{v_{x}}{d x}) (\frac{d x}{d t}) = ((v_{x}) \frac{d v_{x}}{d x}) ... ... ... . (i i)$
$A s ({(v_{x})}_{x}^{2}) + ({(v_{y})}_{y}^{2}) = v^{2},$
$(2 v_{x}) (d v_{x}) + ((2 v_{y}) (d v_{y})) = 0$
$g i v \in g ((v_{x}) (d v_{x})) = - (v_{y}) (d v_{y}) ... . . (i i i)$
$F r o m (i), (i i) and (i i i),$
$((v_{y}) \frac{d v_{y}}{d x}) = \frac{λ (v_{y})}{x}$
$or, \frac{d x}{x} = (d \frac{v_{y}}{λ}) .$
$I n i t i a l l y x = x_{0} and v_{y} = 0 . A t min i μ m s e p a r a t i o n o m$
$t h e w i r e, v_{x} = 0 s o t {ˆ v}_{y} = - v .$
$T h u s (\int_{x_{0}}^{x}) (\frac{d x}{x}) = ({(\int_{0})}_{0}^{- v}) (\frac{d v_{y}}{λ})$
$or, I n (\frac{x}{x_{0}}) = (- \frac{v}{λ})$
or, x = (x_0) (e^(-v/lambda))= (x_0) (e ^(- 2pi m v /((mu_0)qi))

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

HC VERMA-MAGNETIC FIELD DUE TO CURRENT-worked out examples

Home
Ask Doubt
Profile