Figure shows a light platform on which a man of mass M is standing and holding a string passing over a system of ideal pulleys. Another mass m is hanging as shown in fig. Find the force the man has to exert to maintain the equlibrium of system, and find the force exerted by the platform on the man. Also find the ratio of M/m.
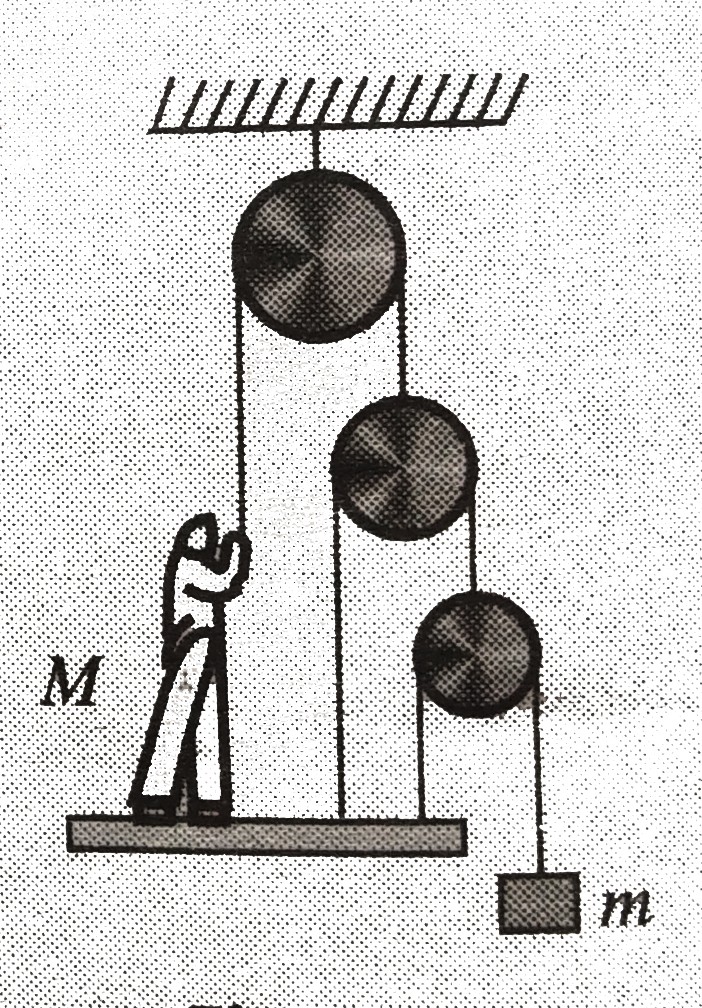
Let the man exertes force F on string
2F=F+N+mg ..(i)
and F+N=Mg ..(ii)

from eq. (i) and (ii): F=(M+m)g2andN=(M−m)g2

Also N=3mg …(iii)
For the whole system of (man + block +pulley)
2F=Mg+mg ...(iv)
From (i) and (iii) F=4mg, also we can get M=7m.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.319videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.413videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
A man of mass M is standing on a plank kept in a box. The plank and box as a whole has mass m. A light string passing over a fixed smooth pulley connects the man and box. If the box remains stationary, find the tension in the string and the force exerted by the man on the plank.
 View Solution
View SolutionA man of mass m=2kg is standing on a platform of mass M=5kg, then at any instant.
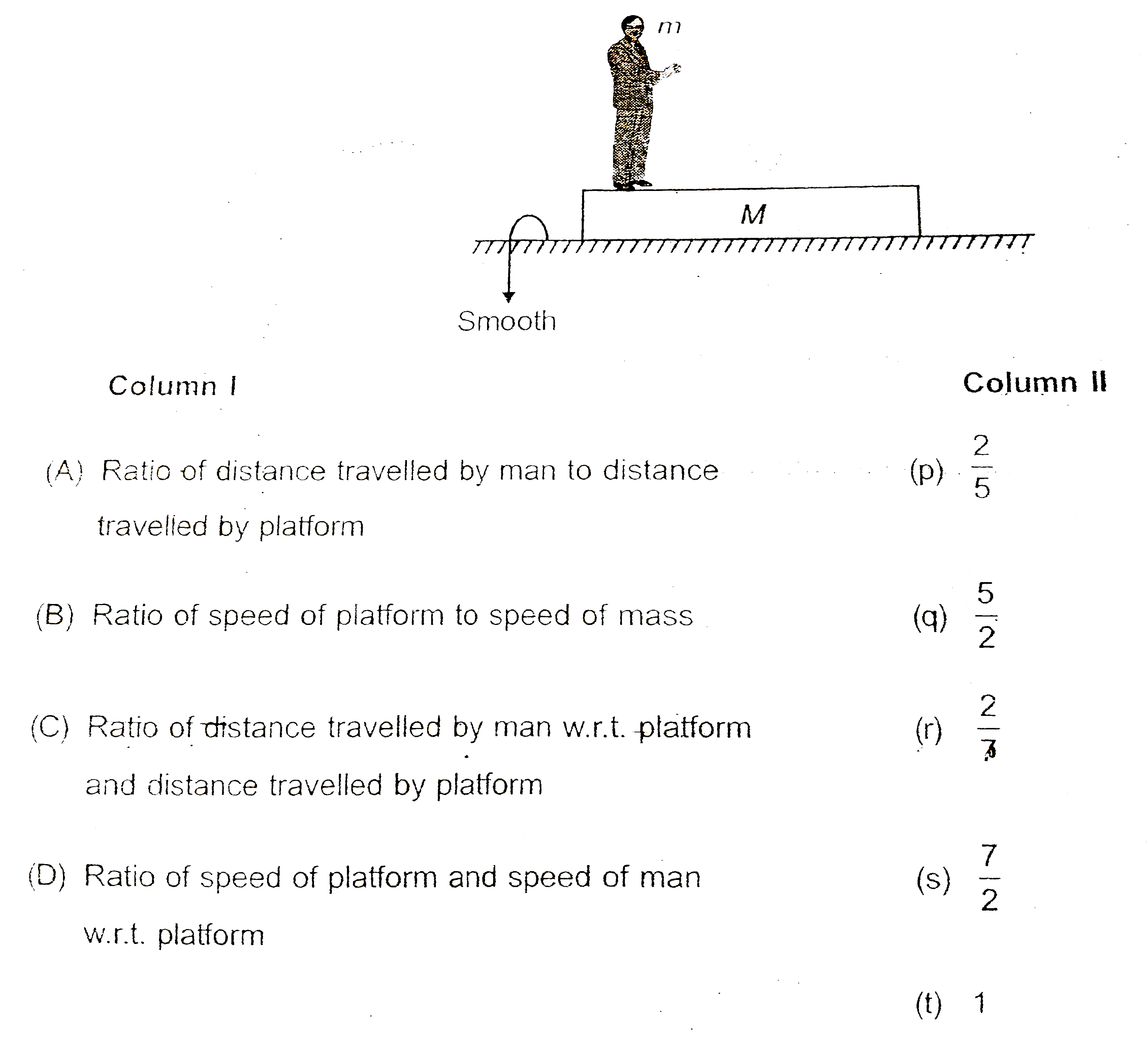 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
Two masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
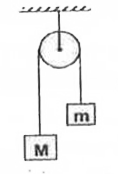 Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above - Question 2 - Select One
In the following figure, the object of mass m is held at rest by a horizontal force as shown. The force exerted by the string on the block is -
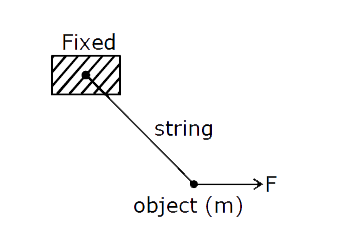 AFBmgCF+mgD√F2+m2g2
AFBmgCF+mgD√F2+m2g2 - Question 3 - Select One
Two bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
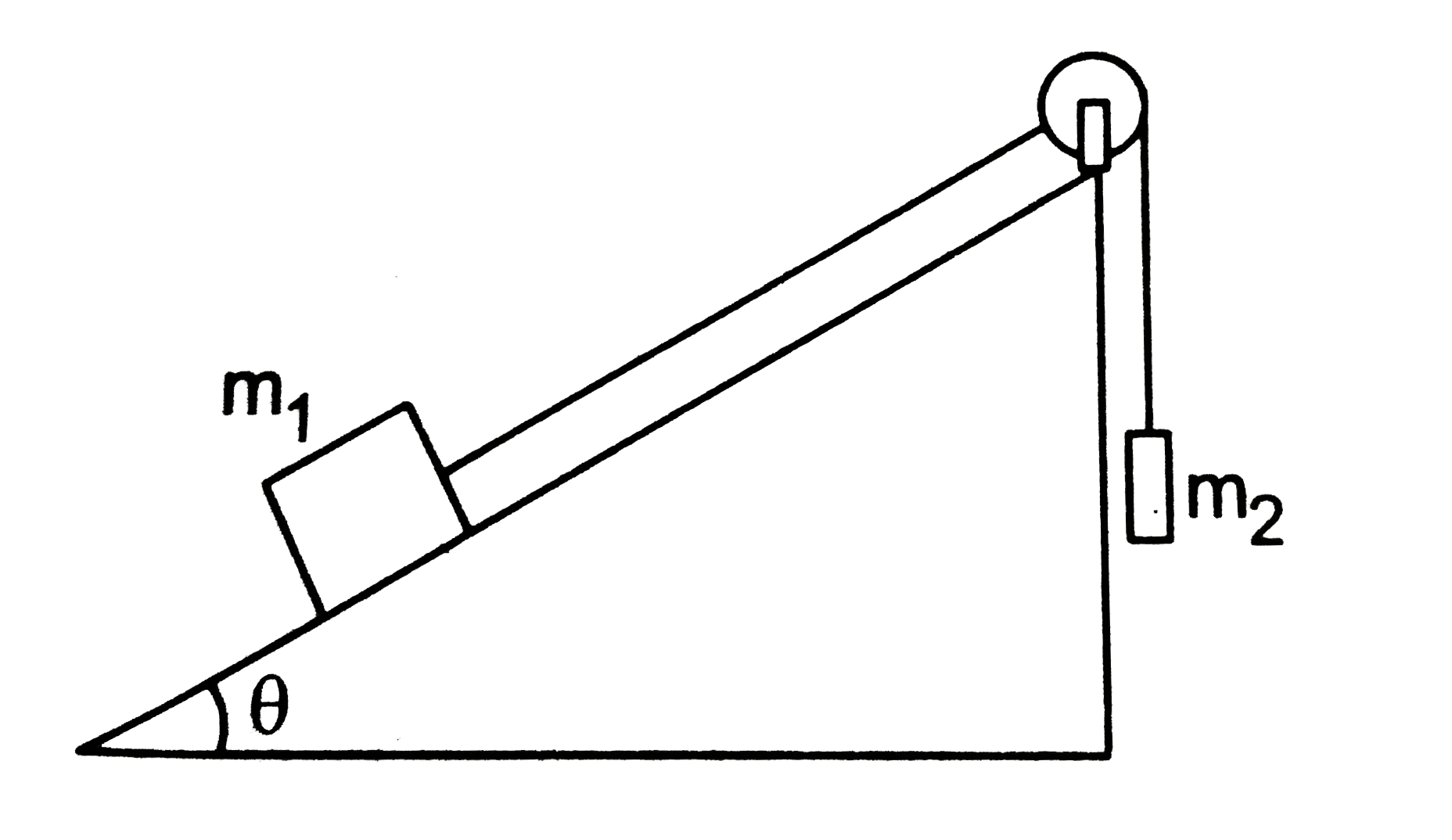 Asinθ=2m2m1 , N=m1gcosθBsinθ=m2m1 , N=m1gcosθCsinθ=m2m1 , N=m1gsinθDsinθ=m2m1 , N=4m1gcosθ
Asinθ=2m2m1 , N=m1gcosθBsinθ=m2m1 , N=m1gcosθCsinθ=m2m1 , N=m1gsinθDsinθ=m2m1 , N=4m1gcosθ
As shown in figure pulley is ideal and strings are massless.If mass m of hanging block is the minimum mass to set the equilibrium of system, then -
 View Solution
View SolutionA mass string going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given
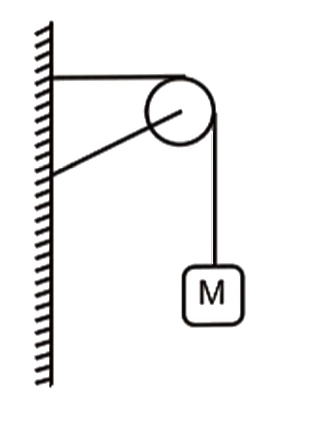 View Solution
View SolutionConsider the situation as shown in the figure. The boy of mass M holds the light rope and the system is at rest. If m is mass of the box, find the force exerted by the boy on the rope and contact force beteween the boy and the box.
 View Solution
View SolutionIn the arrangement shown in figure, what should be the mass of block A so that the system remains at rest. Also find force exerted by string on the pulley Q.
(g=10m/s2)
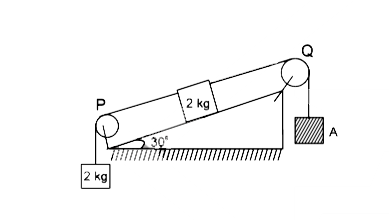 View Solution
View SolutionTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
 View Solution
View Solution

