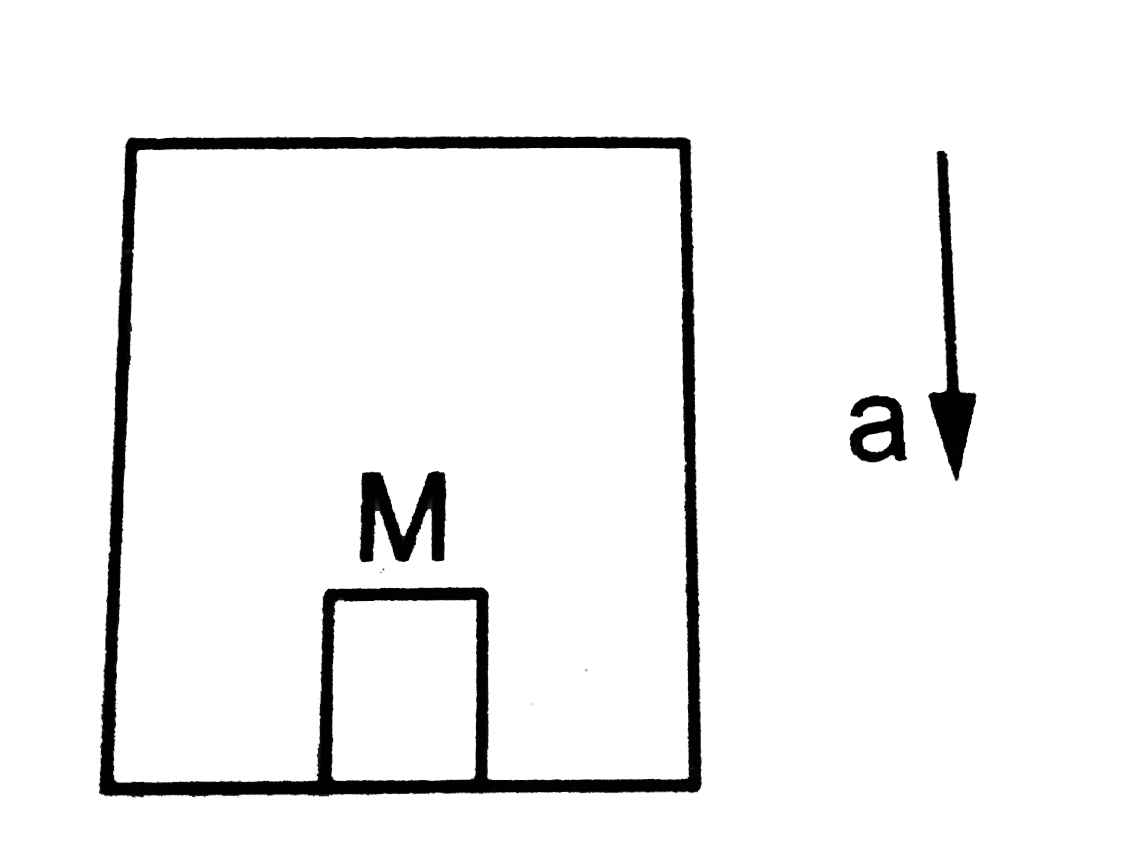
In fig. the block of mass M is at rest on the floor . At what acceleration with which should a boy of mass m climb along the rope of negligible mass so as to lift the block from the floor?
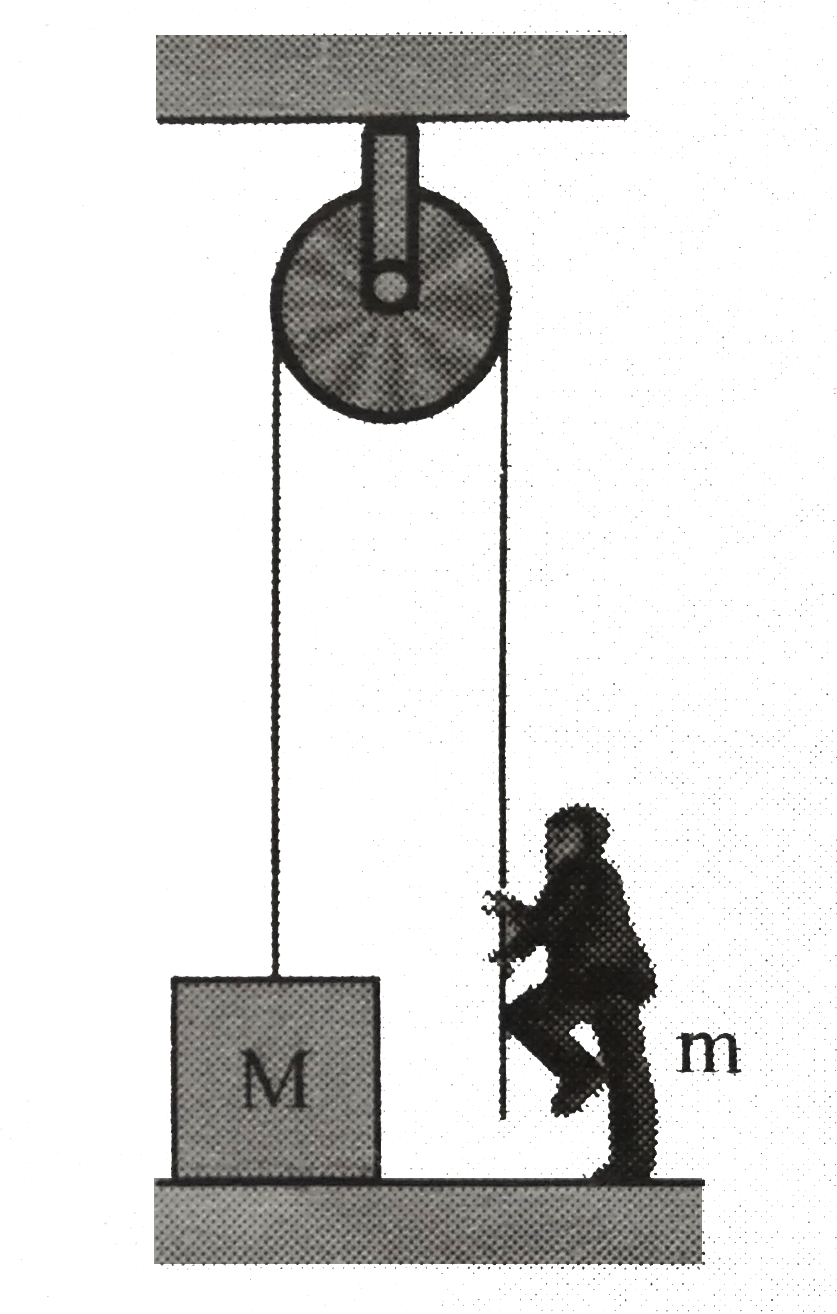
Equation of motion for M:
Since M is stationary, T−Mg=0
⇒T=Mg …(i)
Since the boy moves up with an acceleration a,
T−mg=ma
⇒T=m(g+a)…(ii)
Equating (i) and (ii), we obtain
Mg=m(g+a)
⇒a=(Mm−1)g
that means, if a>(Mm−1)g, block M can be lifted from floor.

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.319videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.413videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
Knowledge Check
- Question 1 - Select One
Block A of mass 35 kg is resting on a frictionless floor.
 A0.8ms−2B2.4ms−2C0.4ms−2D4.4ms−2
A0.8ms−2B2.4ms−2C0.4ms−2D4.4ms−2 - Question 2 - Select One
A rope of negligible mass passes over a pulley of negligible mass attached to the ceiling, as shown in figure. One end of the rope is held by Student A of mass 70kg, who is at rest on the floor. The opposite end of the rope is held by Student B of mass 60kg, who is suspended at rest above the floor. The minimum acceleration a0 with which the Student B should climb up the rope to lift the Student A upward off the floor. (g=10m/s2)
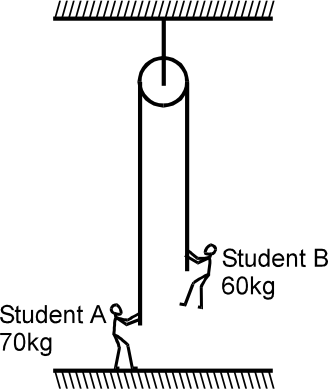 A13m/s2B23m/s2C43m/s2D53m/s2
A13m/s2B23m/s2C43m/s2D53m/s2 - Question 3 - Select One
With what acceleration 'a' should the box of figure moving up so that the block of mass M exerts a force 7Mg/4 on the floor of the box?
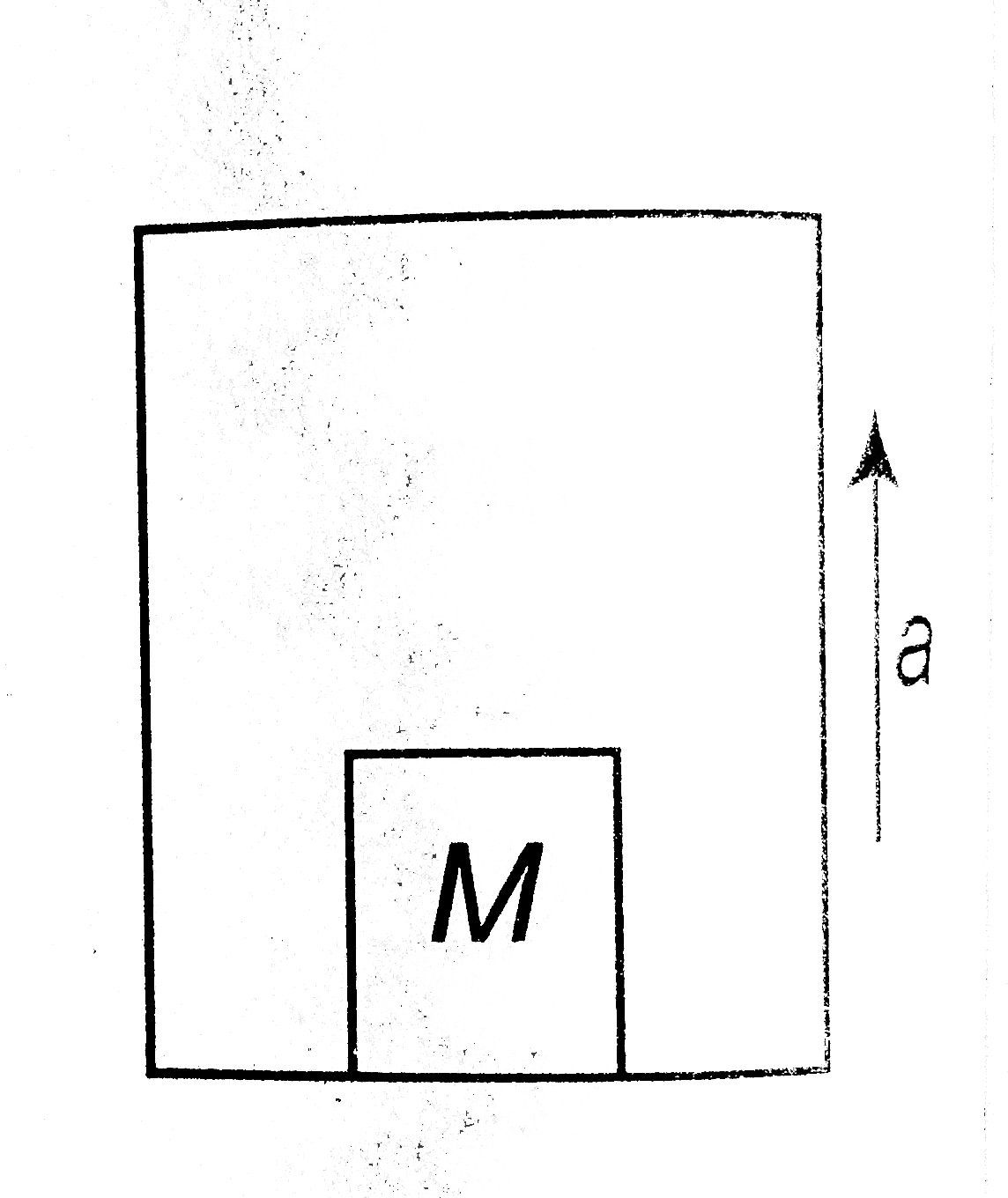 Ag/4Bg/2C3g/4D4g
Ag/4Bg/2C3g/4D4g
In the arrangement shown in the fig. a monkey of mass M keeps itself as well as block A at rest by firmly holding the rope. Rope is massless and the pulley is ideal. Height of the monkey and block A from the floor is h and 2h respectively [h = 2.5 m]
(a) The monkey loosens its grip on the rope and slides down to the floor. At what height from the ground is block A at the instant the money hits the ground?
(b) Another block of mass equal to that of A is stuck to the block A and the system is released. The monkey decides to keep itself at height h above the ground and it allows the rope to slide through its hand. With what speed will the block strike the ground?
(c) In the situation described in (b), the monkey decides to prevent the block from striking the floor. The monkey remains at height h till the block crosses it. At the instant the block is crossing the monkey it begins climbing up the rope. Find the minimum acceleration of the monkey relative to the rope, so that the block is not able to hit the floor. Do you think that a monkey can climb with such an acceleration? (g=10ms−2)
 View Solution
View SolutionA block of mass 25 kg is raised bu a 50kg man in two different ways as shown in fig. what is the action on the floor by the man in the two cases? If the floor yields to a normal force of 700N, which mode should the man adopt to lift the block without the floor yielding?
 View Solution
View SolutionA block of metal is lying on the floor of a bus. The maximum acceleration which can be given to the bus so that the block may remain at rest, will be -
View SolutionA block of mass 2 kg rests on the floor of an elevator , which is moving down with an acceleration 'g' , then the apparent weight of the block is [ take g = 10m/s2 ]
View SolutionA small block of mass m rests on a smooth wedge of angle θ. With what horizontal accelaration a should the wedge be pulled, as shown in fig, so that the block falls freely?
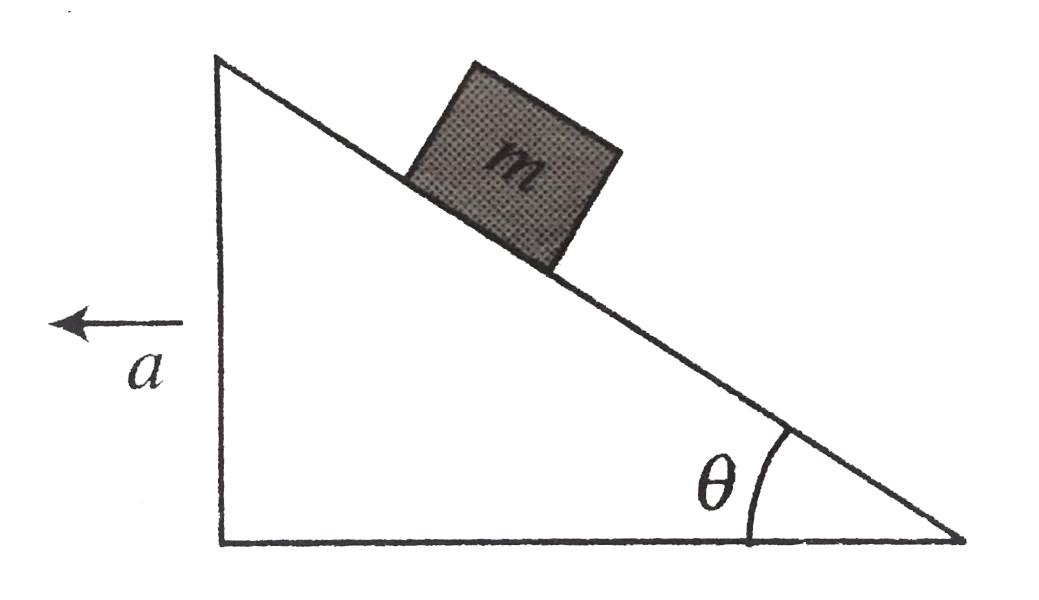 View Solution
View Solution