Figure shows a light rod of length l rigidly atached to a small heavy block ast one end and a hook at the other end. The system is released from rest with the rod in a horizontal position. Thre isa fixed smooth ring at a depth h below the initial position of the hook and the hook gets into the ring as it reaches there. Whast should be the minimum value of h so that the block moves in a complete circle about the ring?

The minimum velocity required to cross the height point c=√2gl
Let the rod relesed from a height h.
Total energy at A=total energy at B
mgh=12mv2
mgh=12m(2gl)
[Because v is the required velocity at B such that the block make a complete circle.
Refer Q=49]
So h=l
Topper's Solved these Questions
Similar Questions
A uniform rod of length L and mass M is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
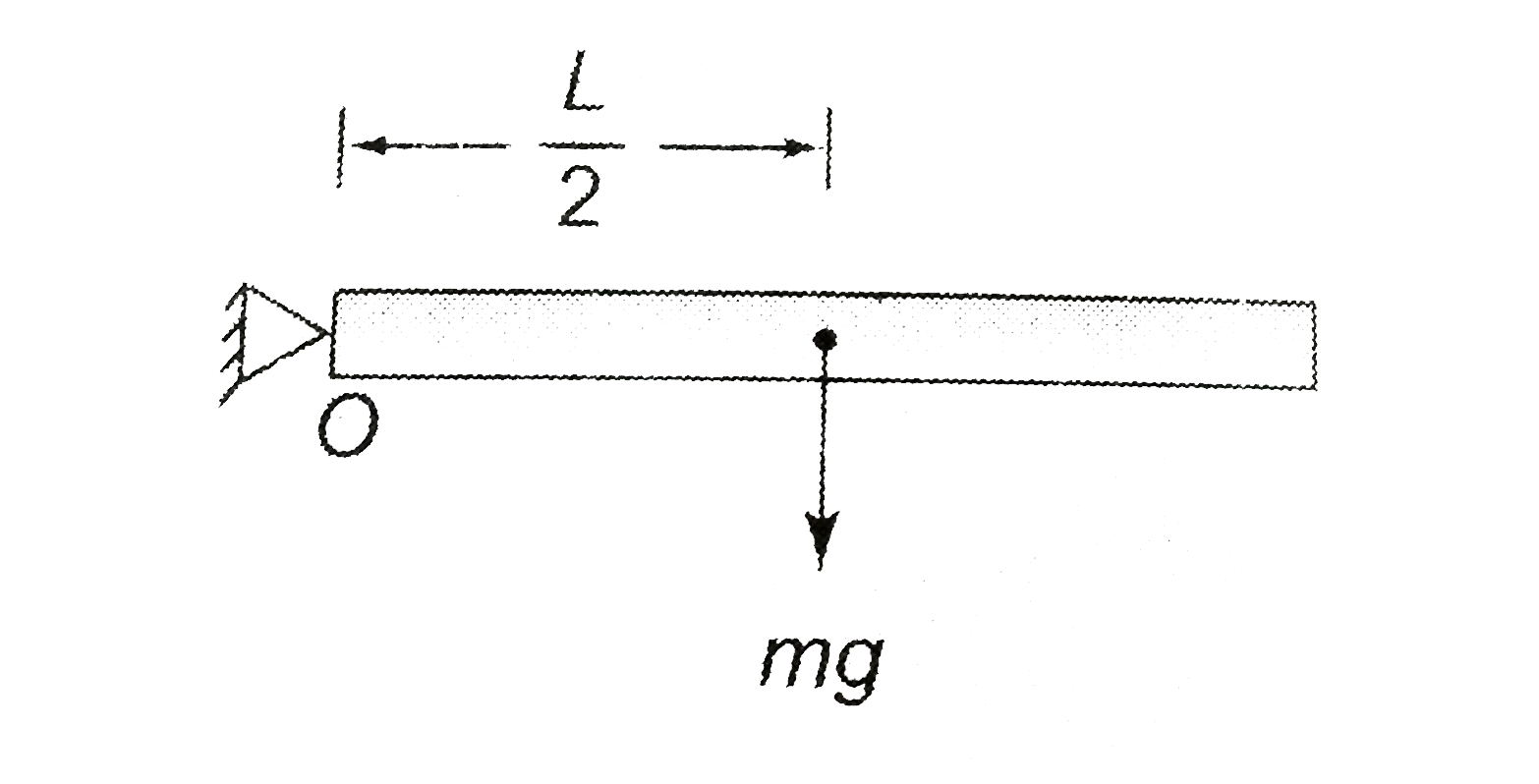
View SolutionA rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?
View Solution
Knowledge Check
In the above problem, if the rod is released from horizontal position, the angular velocity of the rod as it passes the vertical position is (l=length fo rod)
A√12g5lB√2g3lC√3glD√3g7lA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
A√2gLB√3gLC√g2LD√gLA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, When it is in verticle position is
A√2gLB√3gLC√g2LD√gL
A rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA light rigid rod of length 4m is connected rigidly with two identical particles each of mass m=2kg. the free end of the rod is smoothly pivoted at O. The rod is released from rest from its horizontal position at t=0. Find the
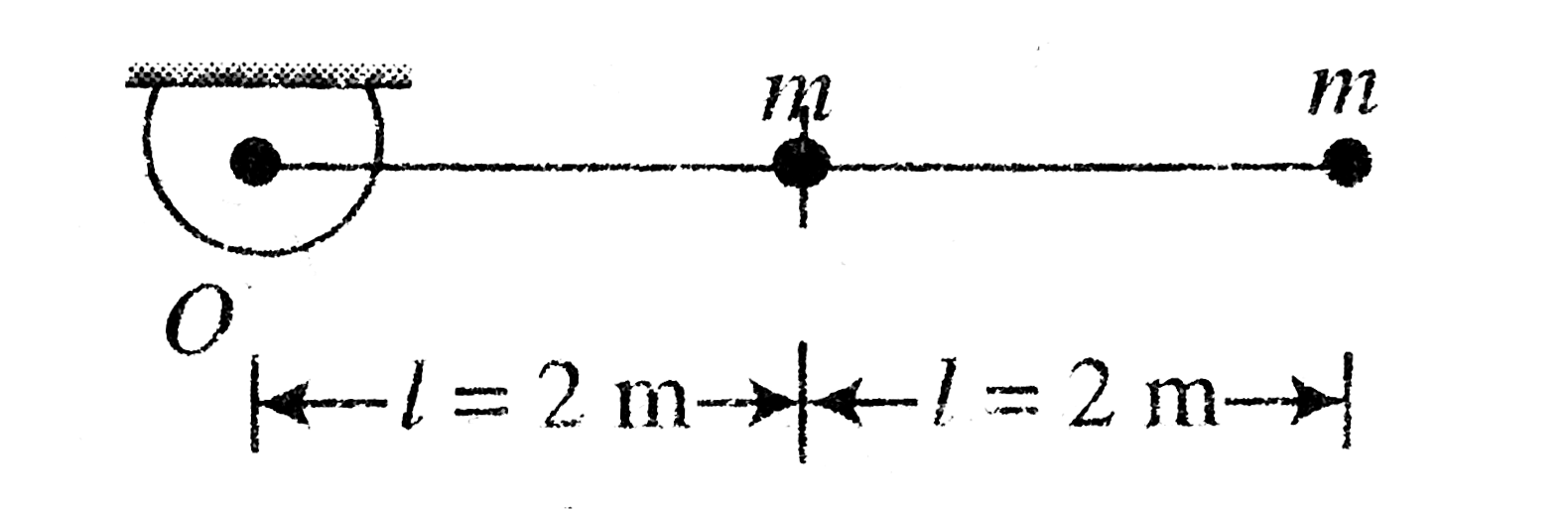
reaction offered by the pivot at t=0 (in N).
View SolutionA uniform slender rod of mass M and length L is pivoted at its end. The rod is released from its nearly vertical position. What is the reaction at the pivot when the rod reaches the horizontal position? If the support is withdrawn at this instant, describe the subsequent motion of the rod.
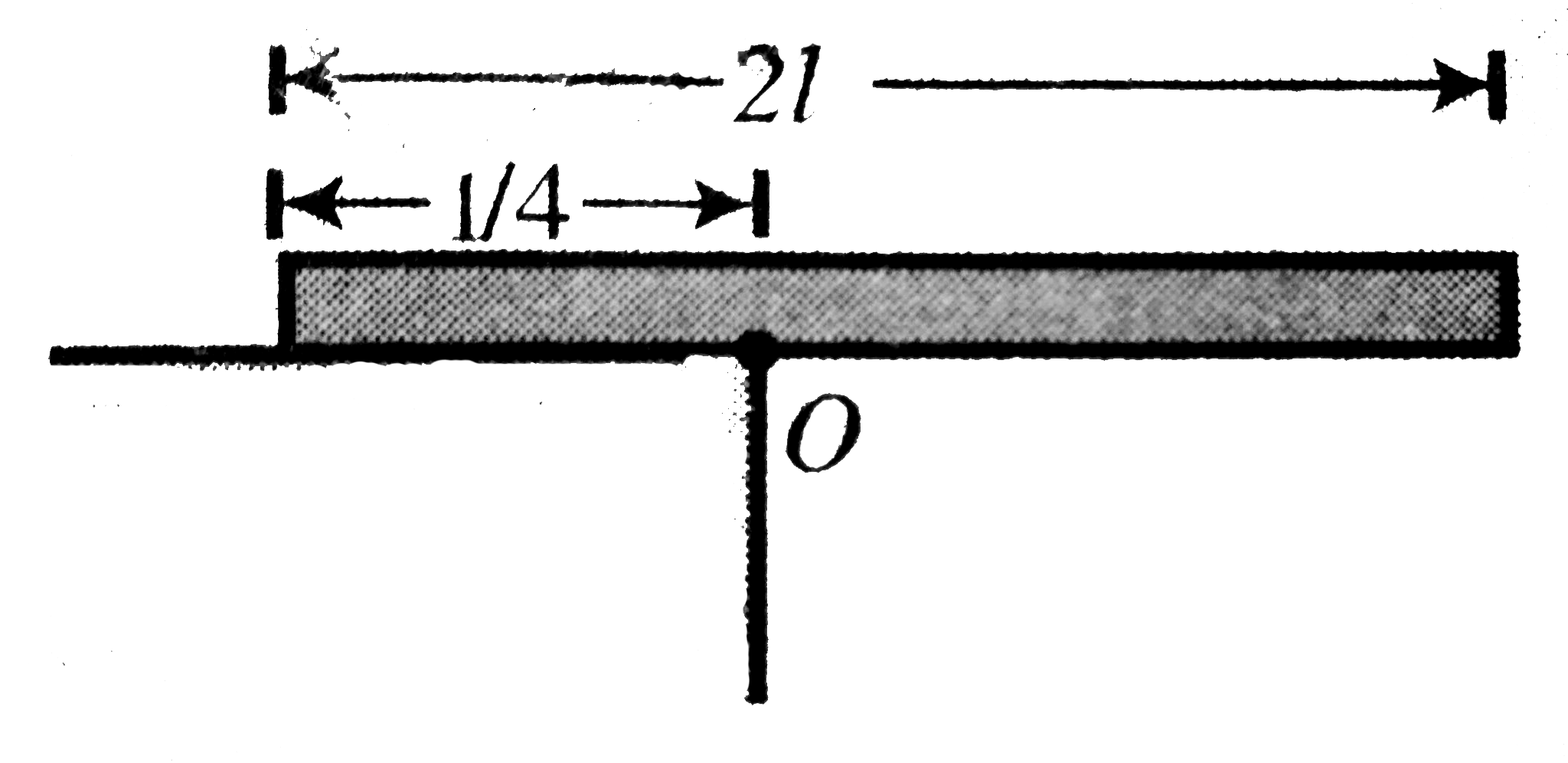
View SolutionOne fourth length of a uniform rod of length 2l and mass m is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.
View SolutionA rod of length L is hinged from one end. It is brought to horizontal position and released. The angular velocity of the rod when it is in vertical position. Is
View Solution
