A heavy particle is usspended by a 1.5 m long string . It is given a horizontal velocityof $\sqrt{57} \frac{m}{s} .$ a. Find the angle made by the string with the upward vertical, when it becomes slack. B. Find the speed of the particle at this instant. c.Find the maximum height reached by the particle over the point of suspension. Take $g = 10 \frac{m}{s^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

$L = 1.5 m, u = \sqrt{57} \frac{m}{\sec}$
a. $m g \cos θ = \frac{m v^{2}}{L}$
$v^{2} = L g \cos θ$
change in K.E.= work done
$\frac{1}{2} m v^{2} - \frac{1}{2} μ^{2} = m g h$
$\to v^{2} - 57 = - 2 \times 1.5 g (1 + \cos θ)$ ……….ii
$\to v^{2} = 57 - 3 g (1 + \cos θ)$

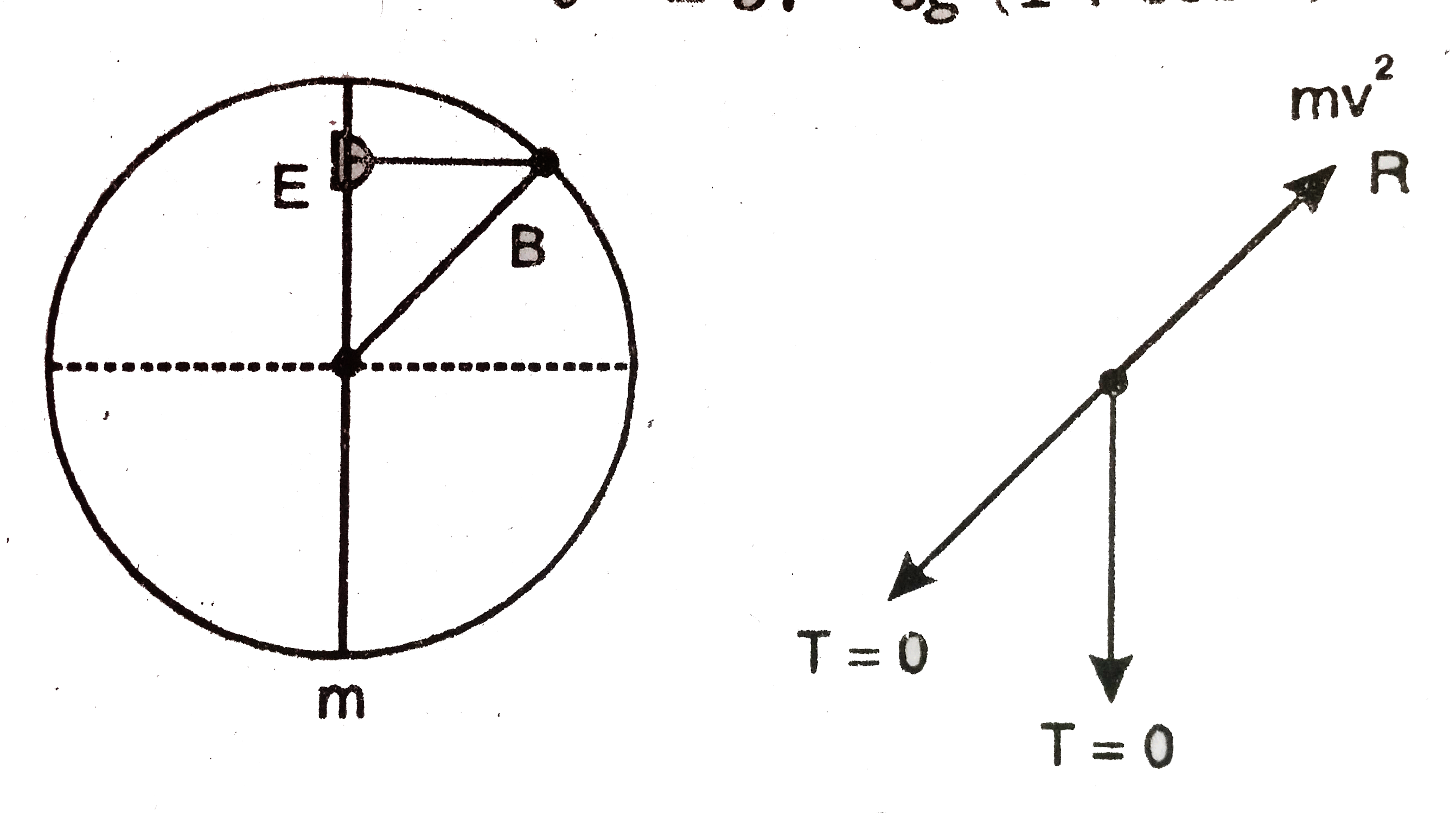
Putting the value of v from equaltion i.
$15 \cos θ - 57 - 3 g (1 + \cos θ)$
$\to 15 \cos θ = 57 - 30 - 30 \cos θ$
$\to 45 \cos θ = 27$
$\to \cos θ = \frac{3}{5}$
$\to θ = \frac{\cos^{- 13}}{5} = 53^{0}$
b. $v = \sqrt{57 - 3 g (1 + \cos θ)}$ from equation i
$\sqrt{9} = \frac{e}{\sec .} < b r > c . a s t h e s t r \in g b e c o m e s l a c k a t p \oint B, t h e p a r t i c \leq w i l l ⋆ t m a k i g n p r o j e c t i o n t i \leq m o t i o n < b r >$ H=OF+DC $< b r >$ =1.5costheta+(u^2sin^2theta)/(2g) $< b r >$ (1.5)xx3/5xx(9xx(0.8)^2)/(2xx10) $< b r >$ 1.2m

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the maximum height reached by a particle which is thrown vertically upwards with the velocity of $20 m / s$ (take $g = 10 m / s^{2}$ ).
A40 m
B10 m
C20 m
Dzero
Question 2 - Select One
Velocity of a particle at some instant is $v = (3 ˆ i + 4 ˆ j + 5 ˆ k) m / s$ . Find speed of the particle at this instant.
A12
B7
C-12
D $5 \sqrt{2}$
Question 3 - Select One
A ball is thrown vertically upward in air. When the particle is at a height half of its maximum height its speed is 10 m/s. Then the maximum height attained by the particle is
A20 m
B15 m
C10 m
D8 m

HC VERMA-WORK AND ENERGY-Exercises

Home
Ask Doubt
Profile