Figure shows a potentiometer with a cell of 2.0 V and internal resistance 0.40 Ω maintaining a potential drop across the resistor wire AB. A standard cell which maintains a constant emf of 1.02 V (for very moderate currents upto a few mA) gives a balance point at 67.3 cm length of the wire. To ensure very low currents drawn from the standard cell, a very high resistance of 600kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf e and the balance point found similarly, turns out to be at 82.3 cm length of the wire
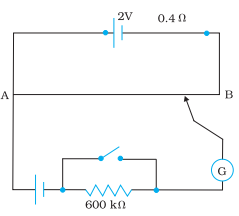
(a) What is the value ε ?
(b) What purpose does the high resistance of 600kΩ have ?
(c) Is the balance point affected by this high resistance?
(d) Is the balance point affected by the internal resistance of the
driver cell?
(e) Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0V instead of 2.0V?
(f) Would the circuit work well for determining an extremely small emf, say of the order of a few mV (such as the typical emf of a thermo-couple)? If not, how will you modify the circuit?
(a) Constant emf of the given standard cell, E1=1.02V
Balance point on the wire, l1=67.3 cm
A cell of unknown emf, ε, replaced the standard cell. Therefore, new balance point on the wire, l=82.3 cm
The relation connecting emf and balance point is,
E1l1=εl
ε=ll1×E1
=82.367.3×1.02=1.247 V
The value of unknown emfits 1.247 V
(b) The purpose of using the high resistance of 600kΩ is to reduce the current through the galvanometer when the movable contact is far from the balance point
(c) The balance point is not affected by the presence of high resistance
(d) The point is not affected by the internal resistance of the driver cell
(e) The method would not work if the driver cell of the potentiometer had an emf of 1.0 V instead of 2.0 V. This is because if the emf of the driver cell of the potentiometer is less than the emf of the other cell, then there would be no balance point on the wire.
(f) The circuit would not work well for determining an extremely small emf. As the circuit would be unstable, the balance point would be close to end A. Hence, there would be a large percentage of error.
The given circuit can be modified if a series resistances is connected with the wire AB. the potential drop acorss AB is slightly greater than the emf measured. The percentage error would be small.
Topper's Solved these Questions
Similar Questions
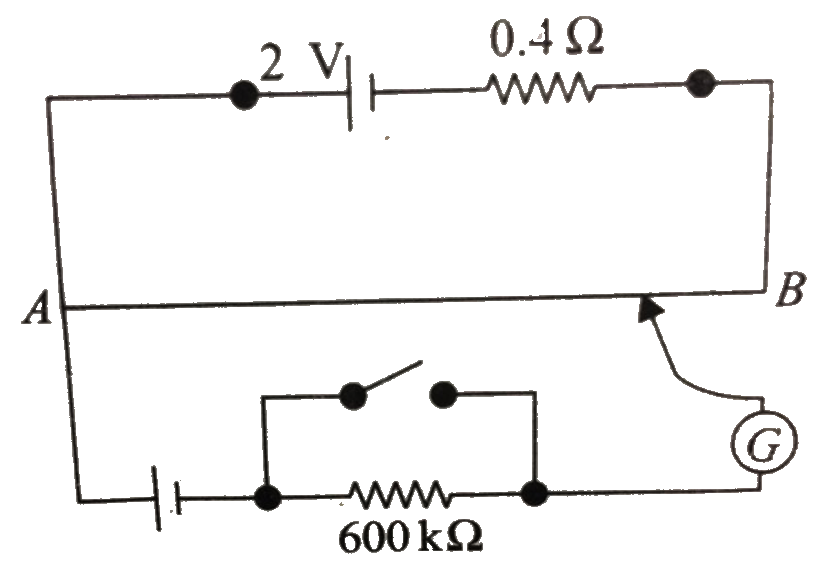
Figure 6.36 shows a potentiometer with a cell of emf 2.0V and internal resistance 0.4Ω maintaining a potential drop across the resistor wire AB. A standard cell that maintains a constant emf of 1.02V (for very moderate current up to emf μA) gives a balance point at 67.3cm length of the wire. To ensure very low current is drawn the standard cell, a very high resistance of 600kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf ε and the balance point found, similary, turns out to be at 82.3cm length of the wire.
a. What is the value of ε?
b.What purpose does the high resistance of 600kΩ have?
c. Is the balance point affected by this high resistance?
d. Is the balance point affected by internal resistance of the driver cell?
e. Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0V instead of 2.0V?
f. Would the circuit work well for determining an extermely small emf, say of the order of a few mV (such as the typical emf of a thermocouple)? If not, how will you modify the circuit ?
View SolutionFigure 6.36 shows a potentiometer with a cell of emf 2.0V and internal resistance 0.4Ω maintaining a potential drop across the resistor wire AB. A standard cell that maintains a constant emf of 1.02V (for very moderate current up to emf μA) gives a balance point at 67.3cm length of the wire. To ensure very low current is drawn the standard cell, a very high resistance of 600kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf ε and the balance point found, similary, turns out to be at 82.3cm length of the wire.
a. What is the value of ε?
b.What purpose does the high resistance of 600kΩ have?
c. Is the balance point affected by this high resistance?
d. Is the balance point affected by internal resistance of the driver cell?
e. Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0V instead of 2.0V?
f. Would the circuit work well for determining an extermely small emf, say of the order of a few mV (such as the typical emf of a thermocouple)? If not, how will you modify the circuit ?

View Solution
Knowledge Check
is made of uniform material and cross-sectional area, and it has uniform resistance per unit length. The potential gradient depends upon the current in the wire.
A potentiometer with a cell of emf 2V and internal resistance 0.4Ω is used across the wire AB. A standard cadmium cell of emf 1.02V gives a balance point at 66cm length of wire. The standard cell is then replaced by a cell of unknows emf e (internal resistance r), and the balance. Point found similarly turns out to be 88cm length of the wire. The length of potentiometer wire AB is 1m.
If the resistance is connected across the cell e, the balancing length willAincreasesBdecreaseCremain sameDnoneis made of uniform material and cross-sectional area, and it has uniform resistance per unit length. The potential gradient depends upon the current in the wire.
A potentiometer with a cell of emf 2V and internal resistance 0.4Ω is used across the wire AB. A standard cadmium cell of emf 1.02V gives a balance point at 66cm length of wire. The standard cell is then replaced by a cell of unknows emf e (internal resistance r), and the balance. Point found similarly turns out to be 88cm length of the wire. The length of potentiometer wire AB is 1m.
The reading of the potentiometer, if a 4V battery is used instead of e isA88.3cmB47.3cmC95cmDcannot be calculated
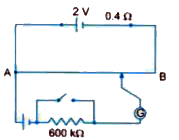
Fig. shows a potentiometer with a cell of 2.0 V and internal resistance 0.40 Ω maintaining a potential drop across the resistor wire AB. A standard cell which maintains a constant emf of 1.02 V (for very moderate currents up to a few mA) gives a balance point at 67.3 cm length of the wire. To ensure very low currents drawn from the standard cell, a very high resistance of 600 kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf and the balance point found similarly, turns out to be at 82.3 cm length of the wire.
(a) What is the value of ε ? (b) What purpose does the high resistance of 600 kΩ have ? (c) Is the balance point affected by this high resistance ? (d) Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0 V instead of 2.0 V? (e) Would the circuit work well for determining an extremely small emf, say of the order of a few mV (such as the typical emf of a thermo-couple) ? If not, how will you modify the circuit ?
View Solution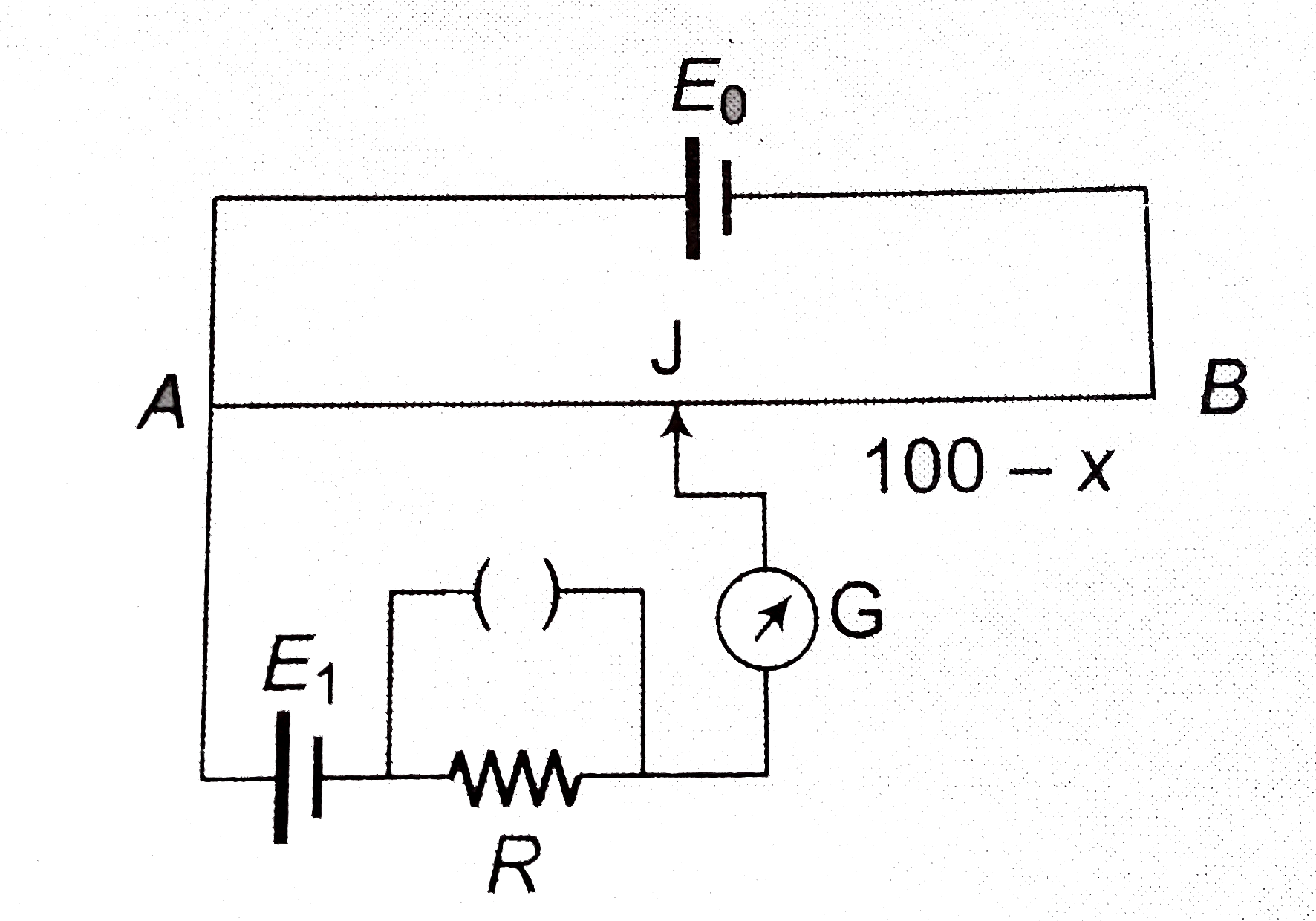
The figure shows a potentiometer using a cell E of emf 2.0V and internal resistance 0.40Ω connected to a resistor wire AB. A standard cell of constant emf of 1.02V gives a balance point a t 67.3cm length of the wire. A very high resistance R=100kΩ is put in with the standard cell. This resistance is shorted by inserting switch S when close to the balance point. The standard cell is then replaced by a cell of unknown emf E and the null point turns out to be 82.3cm length of the wire.
(a) What is the value of E ?
(b) What is the purpose of using the high resistance R ?
( c) Is the null point affected by this high resistance ?
(d) Is the null point affected by the internal resistance of the cell E ?
( e) Would this method work if
(i) the internal resistance of cell E were higher than the resistance of wire AB and
(ii) the emf of cell E were 1.0V instead of 2.0V ?
View SolutionA potentiometer with a cell of EMF 2V and internal resistance 0.4Ω is used across the wire AB. A standard cadmium cell of EMF 1.02V gives a balance point at 66cm length of wire. The standard cell is then replaced by a cell of unknows EMF e (internal resistance r), and the balance. Point found similarly turns out to be 88cm length of the wire. The length of potentiometer wire AB is 1m.
The value of e is
View SolutionIn a potentiometer circuit, the emf of driver cell is 2V and internal resistance is 0.5Ω. The potentiometer wire is 1m long . It is found that a cell of emf 1V and internal resistance 0.5Ω is balanced against 60 cm length of the wire. Calculate the resistance of potentiometer wire.
View SolutionIn a potentiometer circuit, the emf of driver cell is 2V and internal resistance is 0.5Ω. The potentiometer wire is 1m long . It is found that a cell of emf 1V and internal resistance 0.5Ω is balanced against 60 cm length of the wire. Calculate the resistance of potentiometer wire.
View Solutionis made of uniform material and cross-sectional area, and it has uniform resistance per unit length. The potential gradient depends upon the current in the wire.
A potentiometer with a cell of emf 2V and internal resistance 0.4Ω is used across the wire AB. A standard cadmium cell of emf 1.02V gives a balance point at 66cm length of wire. The standard cell is then replaced by a cell of unknows emf e (internal resistance r), and the balance. Point found similarly turns out to be 88cm length of the wire. The length of potentiometer wire AB is 1m.
The reading of the potentiometer, if a 4V battery is used instead of e is
View Solution
