Figure shows a uniform disc of radius $R$ , from which a hole of radius $\frac{R}{2}$ has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.

Video Solution

Text Solution

Verified by Experts

Mass of the cut out disc is
$m = \frac{M}{π R^{2}} \times π {(\frac{R}{2})}^{2} = \frac{M}{4}$
Let centre of the disc is at origin of the coordinates. Then we can write the CM of the system as
$x_{C M} = \frac{\vec{M R} - \vec{m r} + \vec{m r}}{M + m + m} = \frac{M \times 0 - \frac{M}{4} (\frac{- R}{2}) + \frac{M}{4} (\frac{R}{2})}{M - \frac{M}{4} + \frac{M}{4}} = \frac{R}{4}$
$y_{C M} = 0$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.

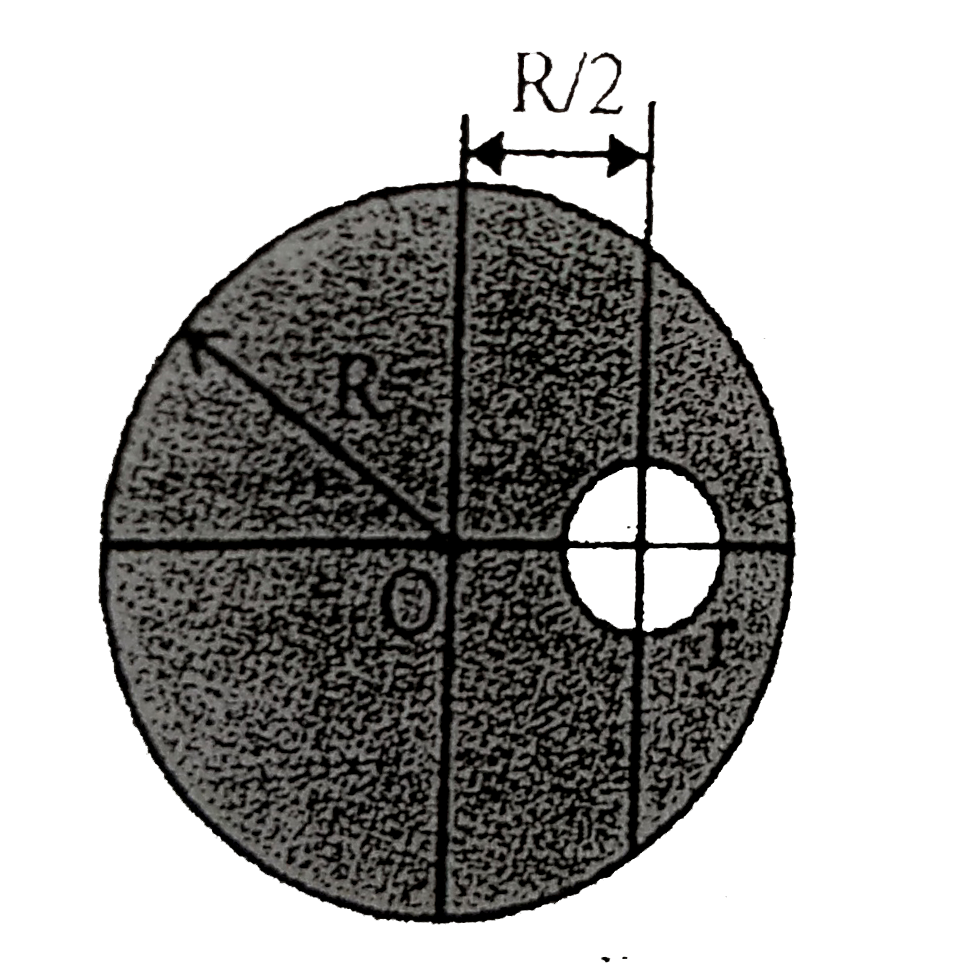A $\frac{R r^{2}}{2 (R^{2} - r^{2})}$ towards right of O
B $\frac{R r^{2}}{2 (R^{2} - r^{2})}$ towards left of O
C $\frac{2 R r^{2}}{(R^{2} + r^{2})}$ towards right of O
D $\frac{2 R r^{2}}{(R^{2} + r^{2})}$ towards left of O
Question 2 - Select One
A paper disc of radius $R$ from which a hole of radius $r$ is cut out is floating in a liquid of the surface tension $S$ . The force on the disc due to the surface tension is
A $S \times 2 π R$
B $S \times 2 π r$
C $S \times 2 π (R - r)$
D $S \times 2 π (R + r)$
Question 3 - Select One
From a circular disc of radius $R$ , a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is $-$

A $\frac{4 R}{3 (π - 2)}$
B $\frac{2 R}{3 (π - 2)}$
C $\frac{5 R}{7 (π - 2)}$
D $\frac{R}{3 (π - 1)}$

CENGAGE PHYSICS-CENTRE OF MASS-INTEGER_TYPE

Home
Ask Doubt
Profile