Figure shows a uniform solid block of mass M and edge lengths a,b and c. Its M.I. about an axis through one edge and perpendicular (as shown) to the large face of the block is
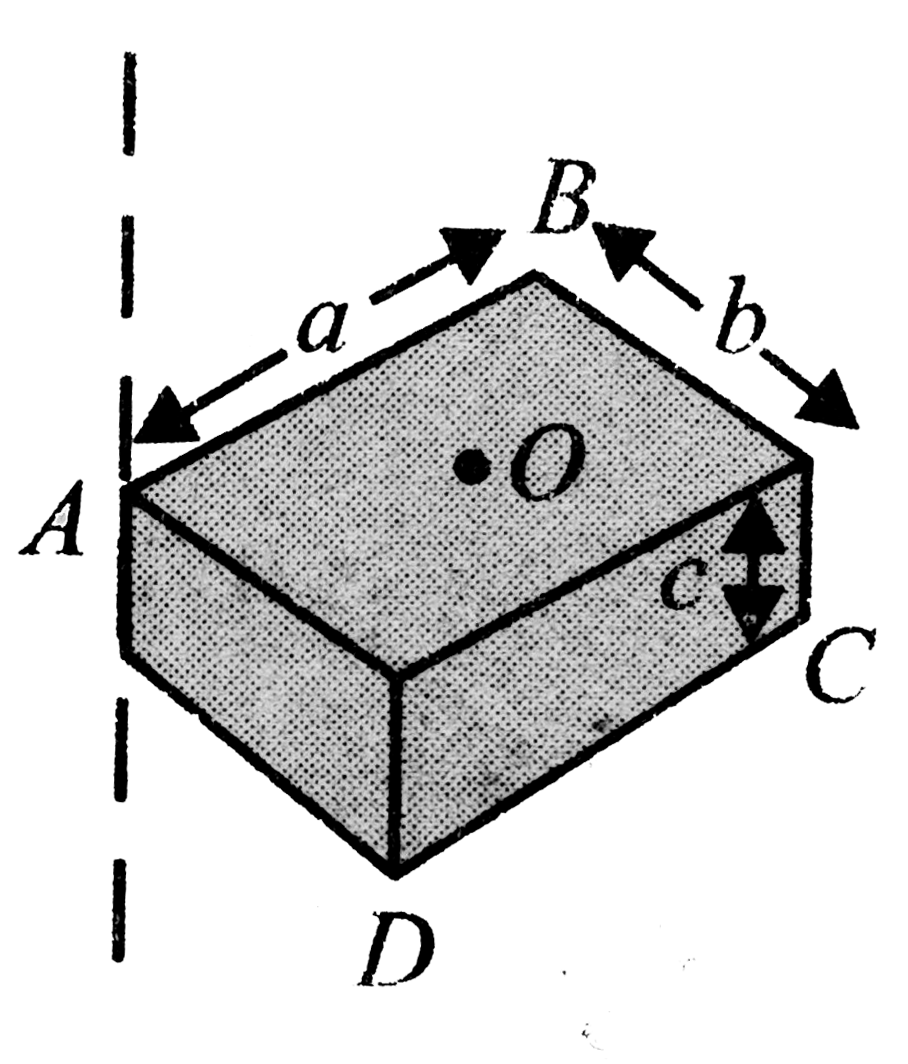
M3(a2+b2)
M4(a2+b2)
7M12(a2+b2)
M12(a2+b2)
The correct Answer is:A
(MI)CG=M(a2+b212)
According to the theorem of parallel axis,
(MI)required axis=(MI)CG+M(OA)2
=M(a2+b23)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
The uniform solid block shown in figure has mass M and edge dimensions a, b, and c. Calculate its rotational inertia about an axis passing through one corner and perpendicular to the large faces.
View SolutionThree thin, uniform, indentical rods each or mass M and length L are joined as shown. Find the M.I. about an axis passing through O and perpendicular to the plane.
View Solution
Knowledge Check
The M.I. of thin uniform rod of mass 'M' and length 'l' about an axis passing through its centre and perpendicular to its length is
AMl2BMl2/3CMl2/2DMl2/12Moment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
A736ML2B748ML2C1148ML2DML212Moment of inertia of a uniform rod of length L and mass M , about an axis pasing through L/4 from one end and perpendicular to its length is
A736ML2B748ML2C1148ML2DML212
Find the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
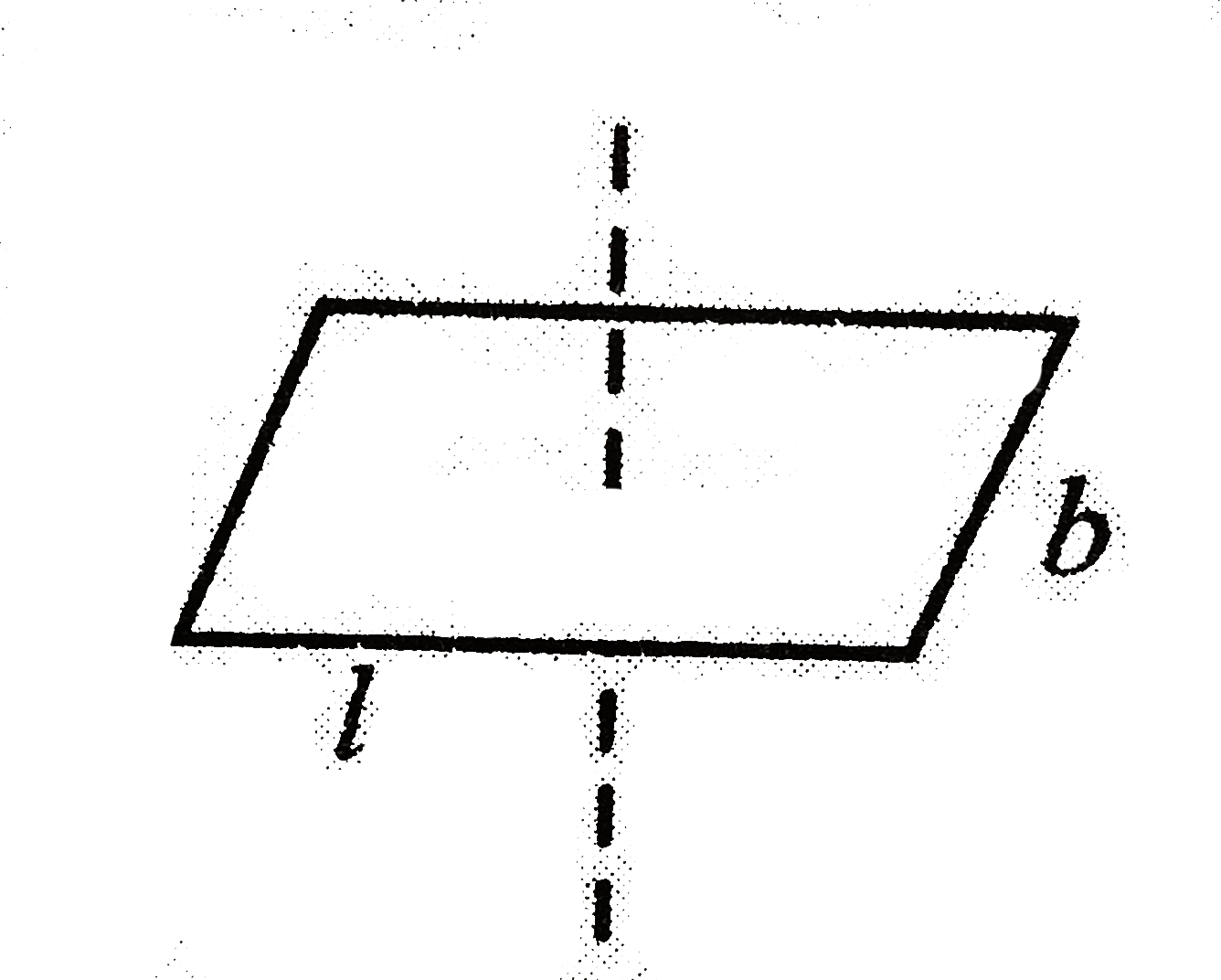
View SolutionFind the moment of inertia of a uniform square plate of mass M and edge of length 'l' about its axis passing through P and perpendicular to it.

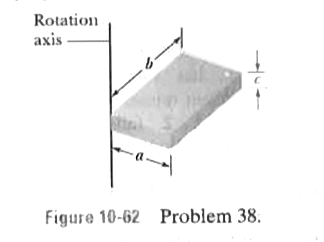
View SolutionThe uniform solid block in Fig. 10-62 has mass 0.172 kg and edge lengths a = 3.5 cm, b = 8.4 cm, and c = 1.4 cm. Calculate its rotational inertia about an axis through one corner and perpendicular to the large faces.
View SolutionThe M.I. of a thin uniform stick of mass 9 gm about an axis passing through one end perpendicular to the length of a meter stick is
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2 R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I, and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2 then
View Solution
