Figure shows the potential energy U(x) of a solid ball that can roll along an x axis. The scale on the U axis is set by Us=100J. The ball is uniform, rolls smoothly, and has a mass of 0.400 kg. It is released at x = 7.0 m headed in the negative direction of the x axis with a mechanical energy of 75 J. (a) If the ball can reach x = 0 m, what is its speed there, and if it cannot, what is its turning point? Suppose, instead, it is headed in the positive direction of the x axis when it is released at x = 70 m with 75 J. (b) If the ball can reach x = 13 m, what is its speed there, and if it cannot, what is its turning point?
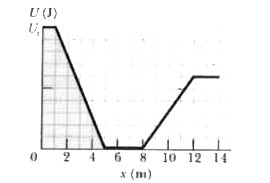
we conclude that there is a turning point (and this is it). The ball, therefore, does not reach the origin, (b) 7.3m/s
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS28videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (More than One Option Correct Type)2videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT4videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))3videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
Similar Questions
Knowledge Check
- Question 1 - Select One
The potential energy of a particle of mass 1 kg in motin along the x-axis is given by
U = 4(1-cos2x)J
Here, x is in meter. The period of small osciallationis (in second) isA2π)BπCπ2D√2π - Question 2 - Select One
The variation of potential energy U of a body moving along x - axis varies with its position (x) as shown in figure
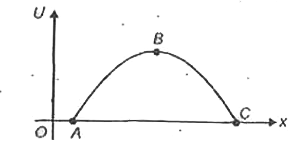
The body is in equilibrium state atAABBCCDBoth A & C - Question 3 - Select One
The variation of potential energy U of a body moving along x - axis varies with its position (x) as shown in figure
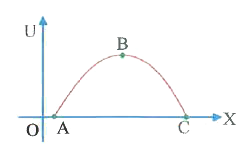
The body is in equilibrium state atAABBCCDBoth A & C
The potential energy of a particle in motion along X axis is given by U=U0−u0 cos ax. The time period of small oscillation is
View SolutionThe potential energy of a particle of mass 1 kg in motin along the x-axis is given by
U = 4(1-cos2x)J
Here, x is in meter. The period of small osciallationis (in second) isView SolutionThe variation of potential energy U of a body moving along x - axis varies with its position (x) as shown in figure

The body is in equilibrium state atView SolutionA partical of mass 2kg is moving on the x−axis with a constant mechanical energy 20J. Its potential energy at any x is U=(16−x2)J where x is in metre. The minimum velocity of particle is :−
View SolutionA partical of mass 2kg is moving on the x−axis with a constant mechanical energy 20J. Its potential energy at any x is U=(16−x2)J where x is in metre. The minimum velocity of particle is :−
View Solution

