A scaffold of mass 65 kg and length 5.2 m is supported in a horizontal position by a vertical cable at each end. A window washer of mass 80 kg stands at a point 1.5 m from one end. What is the tension in (a) the nearer cable and (b) the farther cable?
To solve the problem, we will analyze the forces and torques acting on the scaffold. We will use the principles of static equilibrium, where the sum of forces and the sum of torques acting on the system must equal zero.
Given Data:
- Mass of the scaffold (m_s) = 65 kg
- Length of the scaffold (L) = 5.2 m
- Mass of the window washer (m_w) = 80 kg
- Distance of the window washer from one end (d_w) = 1.5 m
- Acceleration due to gravity (g) = 10 m/s² (for simplicity)
Step 1: Calculate the weights
1. Weight of the scaffold (W_s) = m_s * g = 65 kg * 10 m/s² = 650 N
2. Weight of the window washer (W_w) = m_w * g = 80 kg * 10 m/s² = 800 N
Step 2: Determine the position of the center of mass of the scaffold
The center of mass of the scaffold is located at its midpoint:
- Center of mass position from one end = L/2 = 5.2 m / 2 = 2.6 m
Step 3: Set up the torque equilibrium equation
We will take torques about the point where the nearer cable (T_A) is attached (let’s call this point A). The distance from point A to the center of mass of the scaffold is 2.6 m, and the distance from point A to the position of the window washer is 1.5 m.
The torques due to the weights and tensions are:
- Torque due to the weight of the scaffold (W_s) = W_s * distance from A = 650 N * 2.6 m
- Torque due to the weight of the window washer (W_w) = W_w * distance from A = 800 N * 1.5 m
- Torque due to the tension in the farther cable (T_B) = T_B * L = T_B * 5.2 m
Setting the sum of torques equal to zero:
TB∗5.2=Ws∗2.6+Ww∗1.5
Step 4: Substitute the values and solve for T_B
Substituting the values:
TB∗5.2=650N∗2.6m+800N∗1.5m
TB∗5.2=1690N+1200N
TB∗5.2=2890N
TB=2890N5.2m
TB=555.77N
Step 5: Calculate the tension in the nearer cable (T_A)
Using the equilibrium of vertical forces:
TA+TB=Ws+Ww
Substituting the known values:
TA+555.77N=650N+800N
TA+555.77N=1450N
TA=1450N−555.77N
TA=894.23N
Final Answers:
(a) The tension in the nearer cable (T_A) is approximately 894.3 N.
(b) The tension in the farther cable (T_B) is approximately 555.8 N.
- Mass of the scaffold (m_s) = 65 kg
- Length of the scaffold (L) = 5.2 m
- Mass of the window washer (m_w) = 80 kg
- Distance of the window washer from one end (d_w) = 1.5 m
- Acceleration due to gravity (g) = 10 m/s² (for simplicity)
1. Weight of the scaffold (W_s) = m_s * g = 65 kg * 10 m/s² = 650 N
2. Weight of the window washer (W_w) = m_w * g = 80 kg * 10 m/s² = 800 N
The center of mass of the scaffold is located at its midpoint:
- Center of mass position from one end = L/2 = 5.2 m / 2 = 2.6 m
We will take torques about the point where the nearer cable (T_A) is attached (let’s call this point A). The distance from point A to the center of mass of the scaffold is 2.6 m, and the distance from point A to the position of the window washer is 1.5 m.
- Torque due to the weight of the scaffold (W_s) = W_s * distance from A = 650 N * 2.6 m
- Torque due to the weight of the window washer (W_w) = W_w * distance from A = 800 N * 1.5 m
- Torque due to the tension in the farther cable (T_B) = T_B * L = T_B * 5.2 m
TB∗5.2=Ws∗2.6+Ww∗1.5
Substituting the values:
TB∗5.2=650N∗2.6m+800N∗1.5m
TB∗5.2=1690N+1200N
TB∗5.2=2890N
TB=2890N5.2m
TB=555.77N
Using the equilibrium of vertical forces:
TA+TB=Ws+Ww
Substituting the known values:
TA+555.77N=650N+800N
TA+555.77N=1450N
TA=1450N−555.77N
TA=894.23N
(a) The tension in the nearer cable (T_A) is approximately 894.3 N.
(b) The tension in the farther cable (T_B) is approximately 555.8 N.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS28videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (More than One Option Correct Type)2videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT4videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))3videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
Similar Questions
A uniform horizontal beam of length L and mass M is attached to a wall by a pin connection. Its far end is supported by a cable that makes an angle θ with the horizontal . If a man of mass 'm' stands at a distance l from the wall , find the tension in the cable in equilibrium.
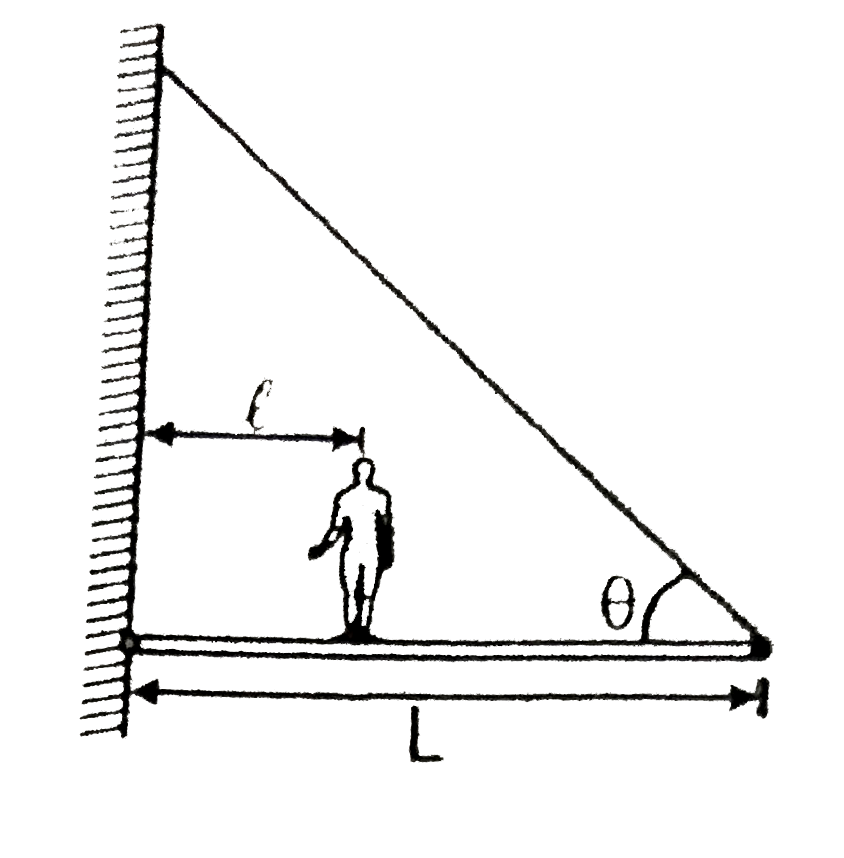 View Solution
View SolutionA uniform bar of mass M and length L is horizontally suspended from the ceiling by two vertical light cables as shown. Cable A is connected 14th distance from the left end of the bar. Cable B is attached at the far right end of the bar. What is the tension in cable A?
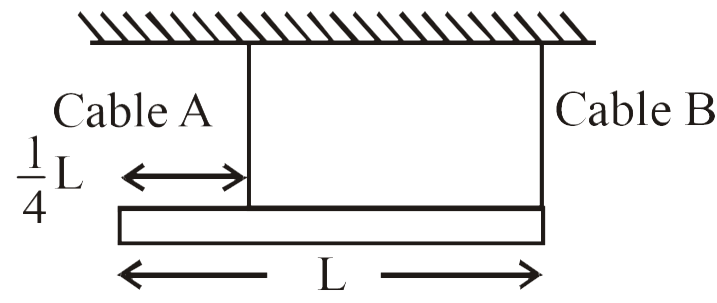 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is
 A15g16B17g16C16g15Dg15
A15g16B17g16C16g15Dg15 - Question 2 - Select One
A steel bar AB of mass 10 kg and length 1 m is kept horizontal by supporting it at the two ends. Two weights of 4 kg and 6 kg are suspended from points of the bar at distances 30 cm and 80 cm respectively from the end A. The reaction at the end A is
A107.8 NB97.8 NC88.2 ND78.2 N - Question 3 - Select One
A uniform rope of mass 0.1 kg and length 2.5 m hangs from ceiling. The speed of transverse wave in the rope at upper end at a point 0.5 m distance from lower end will be
A5 ms−1and2.24ms−1B10 ms−1and3.23ms−1C7.5 ms−1and1.2ms−1DNone of these
A man of mass m=2kg is standing on a platform of mass M=5kg, then at any instant.
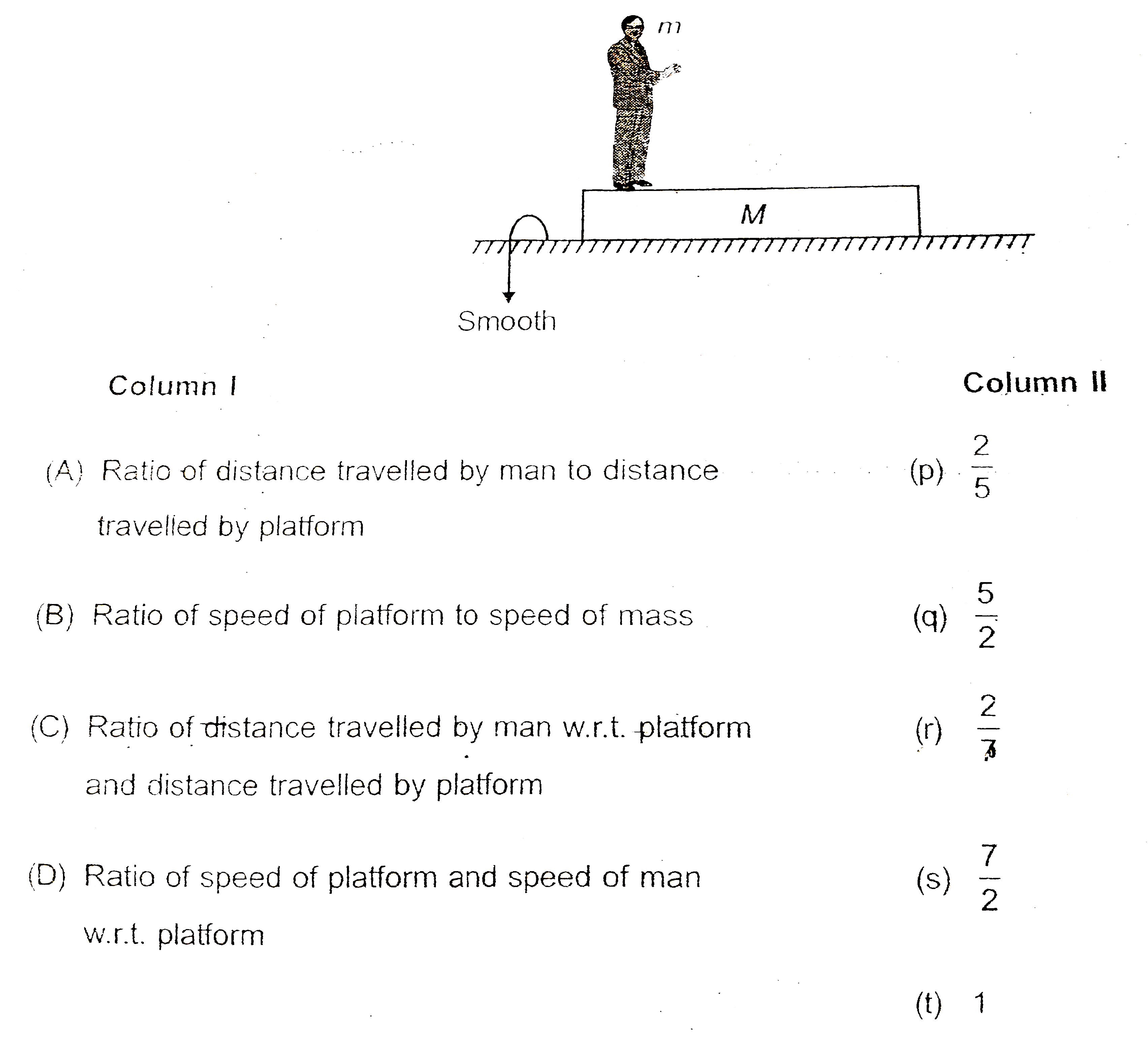 View Solution
View SolutionA plate is in the shape of a quarter cylinder of radius R and length L. This plate is hinged at C to a vertical wall and can rotate freely about C. The end A of the plate is tied to the wall using two horizontal cables the other cables is parallel to OA and the two cables are placed symmetrically). the space between the wall and the plate is filled completely with water (density=ρ) Neglect the weight of the plate and calculate the tension in each cable .
TAke tan−1(π2)=57∘ and cos57∘=12
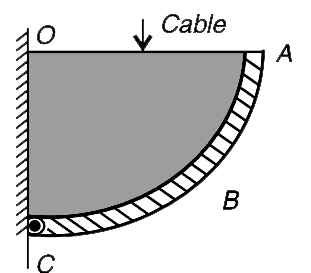 View Solution
View SolutionThe mass of a lift is 600 kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is-
View SolutionA rope of length 4 m having mass 1.5 kg/m lying on a horizontal frictionless surface is pulled at one end by a force of 12N. What is the tension in the rope at a point 1.6 m from the other end?
View SolutionThe mass of a lift if 600kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is :
View Solution

