In Fig. a constant horizontal Force →Fapp of magnitude 10 N is applied to a wheel of mass 10 kg and radius 0.30 m. The wheel rolls smoothly on the horizontal surface, and the acceleration of its center 0.60m/s2. (a) In unit-vec notation, what is the frictional force on the wheel? (b) What is the rotational inertia of the wheel about the rotation axis through its center of mass?
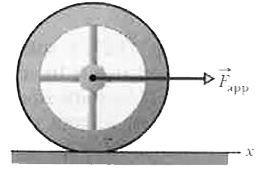
(a) ¯fs=(−4.0N)ˆi, (b) I=0.60kg.m2
Topper's Solved these Questions
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS
28 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (More than One Option Correct Type)
2 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT
4 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))
3 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)
4 Videos
Similar Questions
A constant horizontal force of 10N is applied at the centre of a wheel of mass 10kg and radius 0.30m. The wheel rolls without slipping on the horizontal surface, and the acceleration of the centre of mass is 0.60m/s2.
a. What are the magnitude and direction of the frictional force on the wheel?
b. What is the rotational inertia of the wheel about an axis through its centre of mass and perpendicular to the plane of the wheel?
View SolutionA constant horizontal force of 10N is applied at the centre of a wheel of mass 10kg and radius 0.30m. The wheel rolls without slipping on the horizontal surface, and the acceleration of the centre of mass is 0.60m/s2.
a. What are the magnitude and direction of the frictional force on the wheel?
b. What is the rotational inertia of the wheel about an axis through its centre of mass and perpendicular to the plane of the wheel?
View Solution
Knowledge Check
A wheel of mass 8 kg and radius 40 cm is rolling on a horizontal road with angular velocity 15 rad/s. If moment of inertia of the wheel about its axis is 0.64kgm2, then the rolling kinetic energy of wheel will be
A288 JB216 JC72 JD144 JA torque of 100 N-m acting on a wheel at rest, rotates it through 200 radian in 10 s. What is the moment of inertia of the wheel?
A10 kg-m2B15 kg-m2C20 kg-m2D25 kg-m2A 1.0-kg wheel in the form of a solid disk rolls along a horizontal surface with a speed of 6.0m/s. What is the total kinetic energy of the wheel?
A9.0 JB18 JC27 JD36 J
A wheel is rotating at a speed of 1000 rpm and its KEis106J. What is moment of inertia of the wheel about its axis of rotation ?
View SolutionA wheel is rotating at a speed of 1000 rpm and its KE is 106J. What is moment of inertia of the wheel about its axis of rotation ?
View SolutionA wheel rolls smoothly along a floor while being accelerating horizontally by a force →Fn applied at its top. The wheel has radius R = 0.500 m, mass m = 1.60 kg, and acceleration magnitude a=2.00m/s2. The frictional force on the wheel is in the forward direction and has magnitude f = 1.80 N. What is the rotational inertia of the wheel?
View SolutionA wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.
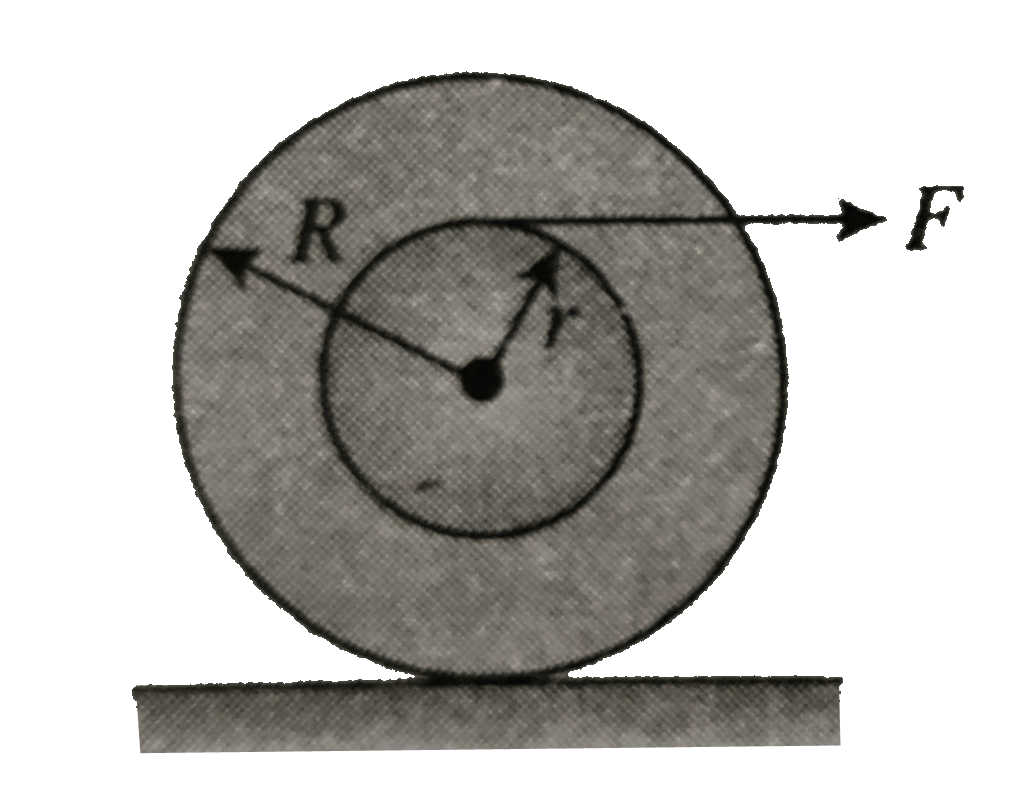
a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.
View SolutionA wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.

a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.
View Solution
