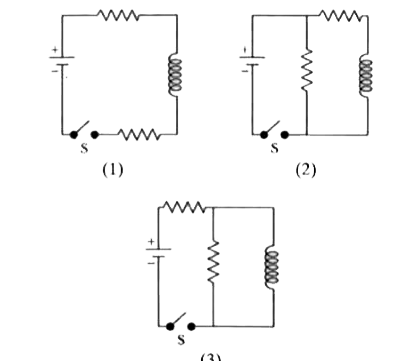
Figure shows three oscillating LC circuit with identical inductors and capacitors.If are the time taken by the circuits I, II, III for fully discharge, then
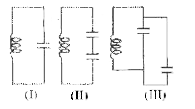
The correct Answer is:C
Time period, .
Clearly .
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In oscillating Lc circuit, the total stored energy is U and maximum charge upon capacitor is Q2, the energy stored in the inductor is
AU2BU4C43UD3U4 - Question 2 - Select One
A capacitor C is connected to two equal resistances as shown in the figure. Consider the following statemets
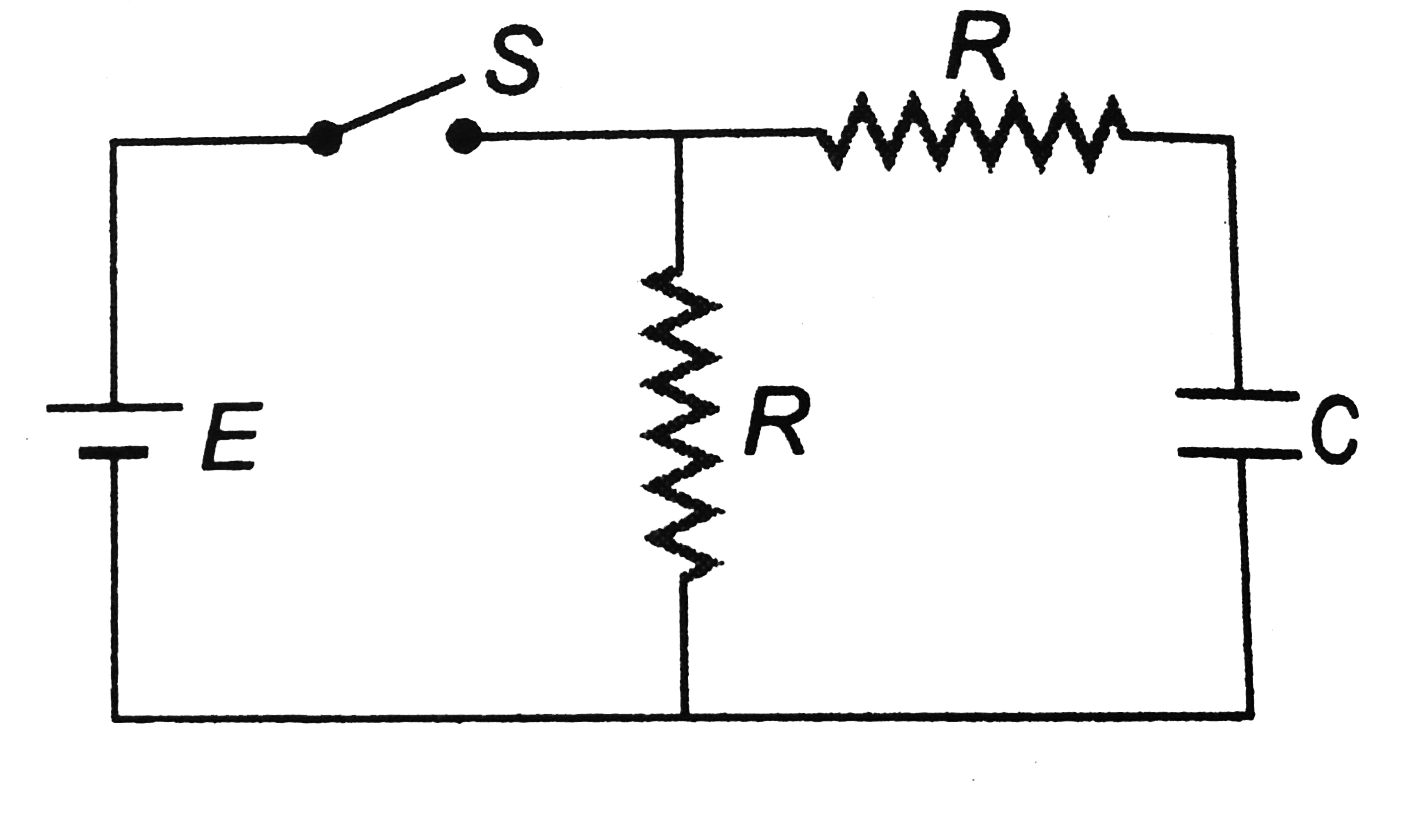
i. At the time of charging of capacitor time constant of the circuit is 2CR
ii. At the time of discharging of the capacitor the time constant of the circuit is CR
iii. At the time of discharging of the capacitor the time constant of the circuit is 2CR
iv At the time of charging of the capacitor the time constant of the circuit is 2CRAstatements i and ii only are correctBstatements ii and iii only are correctCstatements iii and iv only are correctDstatements i and iii only are correct
Figure shows an LCR circuit. When the switch is closed, the currents through resistor R, inductor L, and capacitor C are I1,I2, and I3, respectively. Determine the values of I1,I2, and I3.
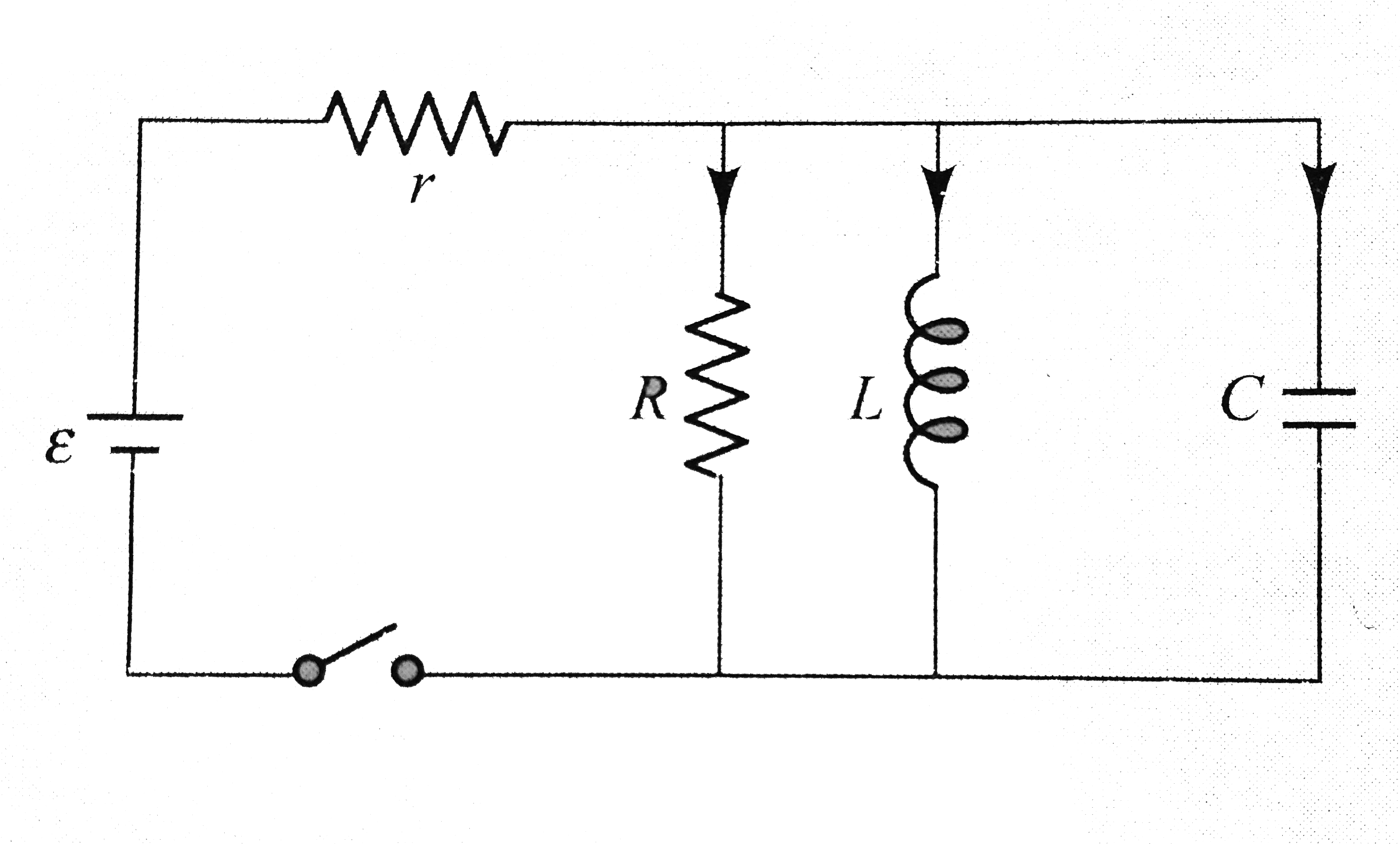
a. at t=0 b. at t=∞View SolutionFigure shows an LCR circuit. When the switch is closed, the currents through resistor R, inductor L, and capacitor C are I1,I2, and I3, respectively. Determine the values of I1,I2, and I3.

a. at t=0 b. at t=∞View SolutionShow that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and and the inductor is constant in time.
View SolutionShow that n the free oscillations of an LC circuit, the sum of energies stored in the capacitor and and the inductor is constant in time.
View SolutionShow that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and and the inductor is constant in time.
View SolutionAn LC circuit contains a 20 mH inductor and a 50 uF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant, the circuit is closed be t = 0.
(a) What is the total energy stored initially ? Is it conserved during LC oscillations ?
(b) What is the natural frequency of the circuit ?
(c) At what time is the energy stored
(i) completely electrical (i.e., stored in the capacitor)?
(ii) completely magnetic (i.e., stored in the inductor)?
(d) At what times is the total energy shared equally between the inductor and the capacitor ?
(e) If a resistor is inserted in the circuit, how much energy is eventually dissipated as heat ?View Solution