In oscillating Lc circuit, the total stored energy is U and maximum charge upon capacitor is , the energy stored in the inductor is
The correct Answer is:D
To solve the problem, we need to find the energy stored in the inductor of an oscillating LC circuit given the total energy U and the maximum charge on the capacitor Q2.
1. Understand the Total Energy in the LC Circuit:
The total energy U in an LC circuit is given by the formula:
U=12Q2C
where Q is the maximum charge on the capacitor and C is the capacitance.
2. Calculate the Energy Stored in the Capacitor:
The energy stored in the capacitor UC when the charge is Q2 is given by:
UC=12(Q/2)2C
Simplifying this, we get:
UC=12Q2/4C=18Q2C
3. Relate the Energy Stored in the Capacitor to Total Energy:
We know from step 1 that:
U=12Q2C
Therefore, we can express UC in terms of U:
UC=18Q2C=14U
4. Calculate the Energy Stored in the Inductor:
The energy stored in the inductor UL can be found by subtracting the energy stored in the capacitor from the total energy:
UL=U−UC
Substituting UC=14U into the equation:
UL=U−14U=34U
5. Final Result:
Thus, the energy stored in the inductor is:
UL=34U
Conclusion:
The energy stored in the inductor is 34U.
The total energy U in an LC circuit is given by the formula:
U=12Q2C
where Q is the maximum charge on the capacitor and C is the capacitance.
The energy stored in the capacitor UC when the charge is Q2 is given by:
UC=12(Q/2)2C
Simplifying this, we get:
UC=12Q2/4C=18Q2C
We know from step 1 that:
U=12Q2C
Therefore, we can express UC in terms of U:
UC=18Q2C=14U
The energy stored in the inductor UL can be found by subtracting the energy stored in the capacitor from the total energy:
UL=U−UC
Substituting UC=14U into the equation:
UL=U−14U=34U
Thus, the energy stored in the inductor is:
UL=34U
The energy stored in the inductor is 34U.
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - B) (Objective Type Questions (One option is correct))
14 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - C ) (Objective Type Questions) ( More than one option are correct)
2 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Try Yourself
15 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION J (Aakash Challengers )
5 Videos
Similar Questions
The energy stored in 4μF capacitors is
View SolutionAn inductor may store energy in
View SolutionMatch the columns

View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View SolutionIn an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
View SolutionIn an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
View SolutionAn L−C circuit consists of an inductor with L=0.0900H and a capacitor of C=4x10−4F. The initial charge on the capacitor is 5.00μC, and the initial current in the inductor is zero.
(a) What is the maximum voltage across the capacitor?
(b) What is the maximum current in the inductor?
(c) What is the maximum energy stored in the inductor?
(d) When the current in the inductor has half its maximum value, what is the charge on the capacitor and what is the energy stored in the inductor?
View SolutionThe total electrostatic energy stored in both the capacitor is
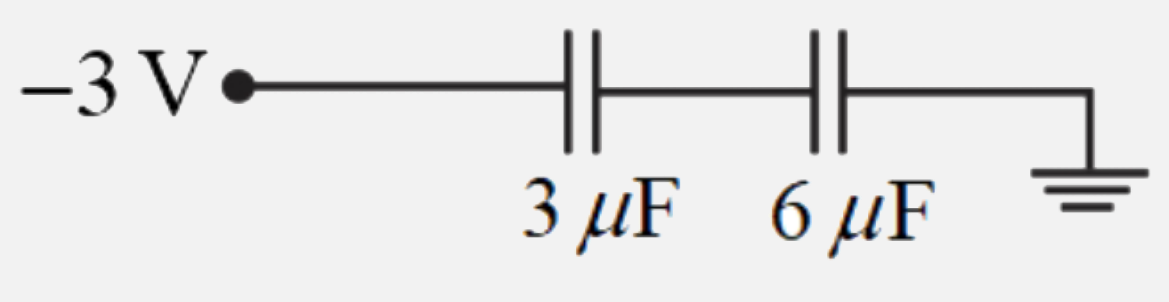
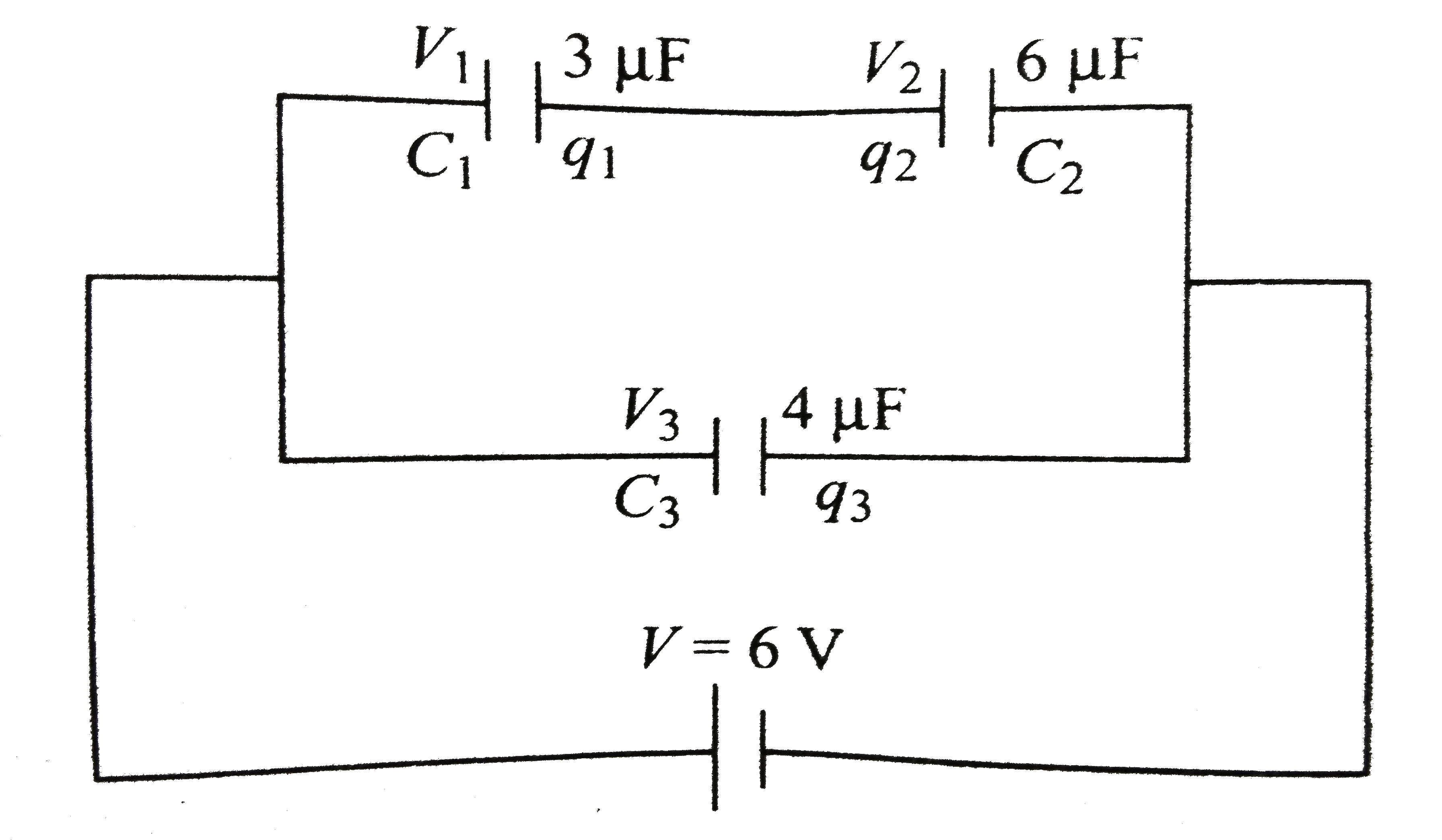
View SolutionThree capacitors of capacitances 3μF, 6μF, and 4μF are connected as shown across a battery of emf 6V.
 .
.
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.
View SolutionA series RLC circuit is connected to an ac generator. The instant at which current in the circuit is zero, the energy stored in the capacitor and inductor are:
View Solution

