Figure shows two charged particles on an x axis : −q=−3.20×10−19C at x=−3.00m and q=3.20×10−19C at = + 3.00 m. What are (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the net electric field produced at point P at y = 4.00 m? (c ) What is the magnitude of the net field if y is doubled ?

(a) 1.38×10−10N/C, (b) 180∘, (c ) 2.77×10−11N/C
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Single Correct Choice Type)
45 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )
3 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
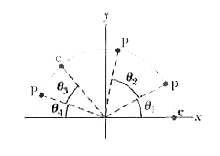
Figure shows an uneven arrangement of electrons (e) and protons (p) on a circular arc of radius r = 2.50 cm, with angles θ1=30.0∘,θ2=50.0∘,θ3=30.0∘, and θ4=20.0∘. What are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the net electric field produced at the net electric field produced at the center of the arc ?
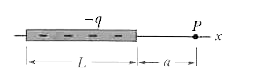
View SolutionIn Fig., a nonconducting rod of length L = 8.15 cm has a charge -q = -4.23 fC uniformly distributed along its length. (a) What is the linear charge density of the rod ? What are the (b) magnitude and (c ) direction (relative to the positive direction of the x axis) of the electric field produced at point P, at distance a = 6.00 cm from the rod ? What is the electric field magnitude produced at distance a = 50 m by (d) the rod and (e) a particle of charge -q = -4.23 fC that we use to replace the rod ? (At that distance, the rod "looks" like a particle.)
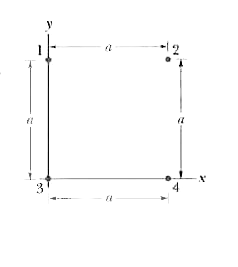
View SolutionIn Fig. , the particles have charges q1=−q2=300nC and q3=−q4=200nC, and distance a = 5.0 cm. What are the (a) magnitude and (b) angle (relative to the +x direction) of the net force on particle 3 ?
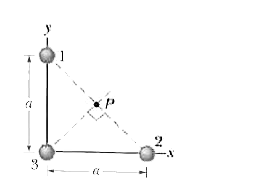
View SolutionIn Fig., the three particles are fixed in place and have charges q1=q2=+5e and q3=+2e. Distance a=3.00μm. What are the (a) magnitude and (b) direction of the net electric field at point P due to the particles ?
View SolutionTwo positively charged particles fixed in place on an x axis. The charges are q1=1.60×10−19Candq2=3.20×10−19C, and the particle separation is R = 0.0200m. What are teh magnitude and direction of the electrostatic force →F12 on particle 1 from particle 2?
View SolutionTwo charged particles are attached to an x axis: Particle 1 of charge −4.00×10−7C is at position x = -5.00 cm and particle 2 of charge +4.00×10−7C is at position x = 10.cm. Midway between the particles, what is their net electric field in unit-vector notation ?
View SolutionFigure shows the three circular arcs centered on the origin of a coordinate system. On each arc, the uniformly distributed charge is given in terms of Q=4.00μC. The radii are given in terms of R = 5.00 cm. What are the (a) magnitude and (b) direction (relative to the positive x direction) of the net electric field at origin due to the arc ?
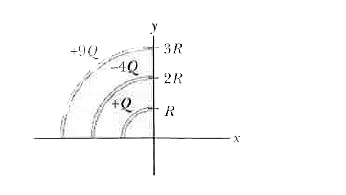
View SolutionTwo charged particles are fixed to an x axis : Particle 1 of charge q1=2.1×10−8C is at position x = 20 cm and particle 2 of charge q2=−4.00q1 is at position x = 70 cm. (a) At what coordinate on the axis (other than at infinity) is the net electric field produced by the two particles equal to zero ? (b) What is the zero-field coordinate if the particles are interchanged ?
View SolutionThe electric potential at points in an xy plane is given by V=(2.00V/m2)x2−(3.00V/m2)y2. What are (a) the magnitude and (b) angle (relative to +x) of the electric field at the point (4.00 m, 2.00 m)?
View SolutionTwo charges +q and -q are kept at (−x1,0)and(x1,0) respectively in the x-y plane. Find the magnitude and direction of the net electric field at the origin (0,0)
View Solution
