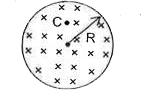
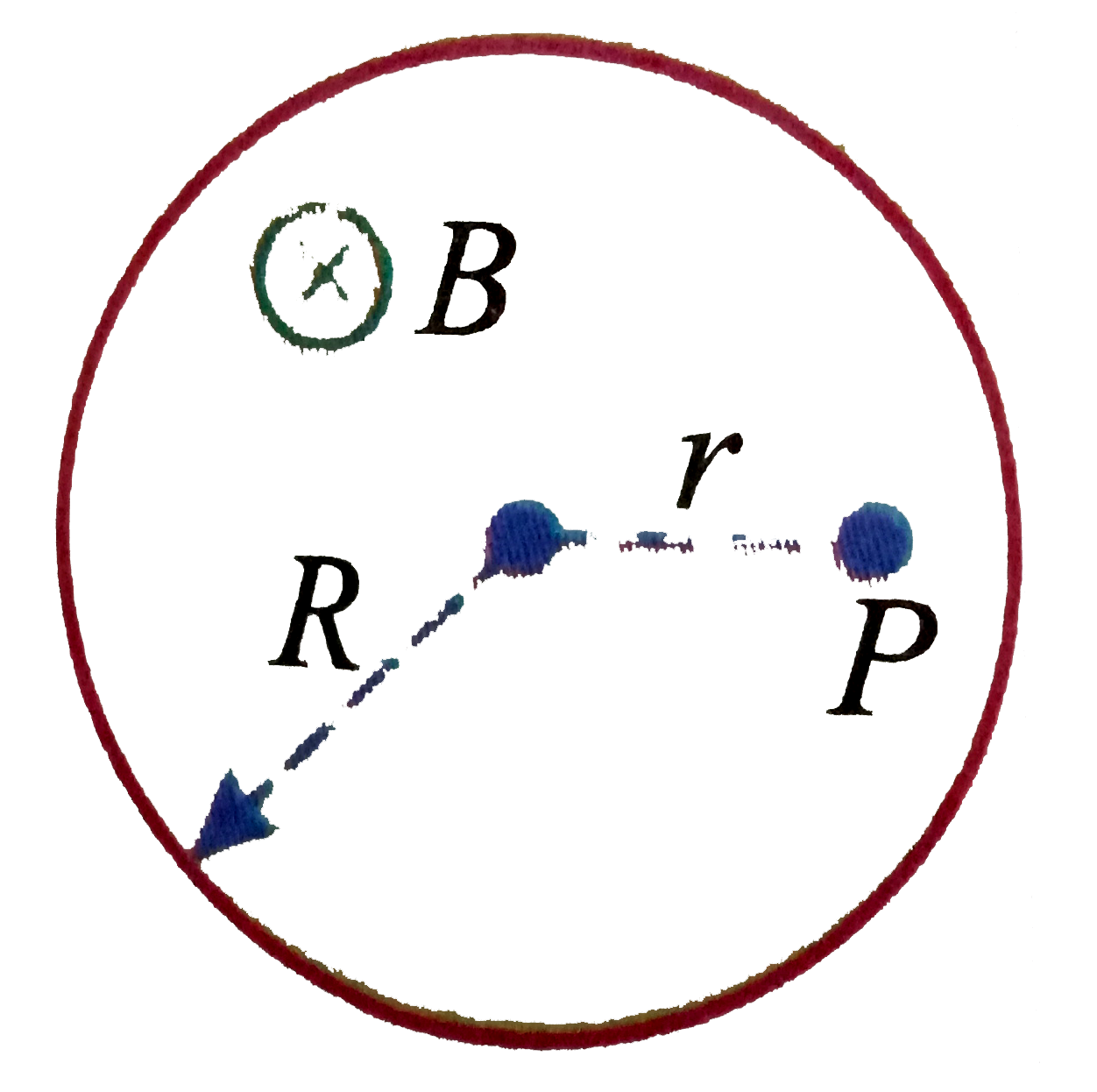
Figures show a uniform magnetic field B condfirned to ta cylinderical bolume of radius R. If B is increasing aty constant rate of 0.01T/s. Instantaneous acceleration experienced by electron at r=10cm (ltR) as shown in the figure.
8.79×10−12m/s2
v8.79×10−11m/s2
8.79×10−10m/s2
8.79×10−09m/s2
The correct Answer is:D
E(2πr)=πr2dbdt⇒E=12rdBdt
a=eEme=e2r(dBdt)me=1.6×10−19×12×0.1×0.019.1×10−3
8.79×10−11m/s2
Topper's Solved these Questions
Similar Questions
Figure shows a uniform magnetic field of induction B confined to a cylindrical volume of radius R. B is increasing at a constant rate of 100 T/s. What is instantaneous acceleration experienced by a charged particle placed at C distant r from centre. Assume r = 5 m.
(Given qm=1.6×10−2 C/kg)
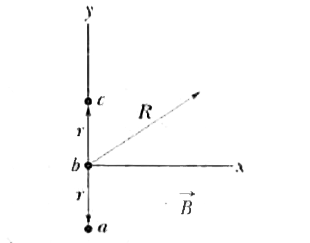
View SolutionFigure 30-61 shows a uniform magnetic field →B confined to a cylindrical volume of radius R. The magnitude of →B is decreasing at a constant rate of 10 mT/s. In unit-vector notation, what is the initial acceleration of an electron released at (a) point a (radial distance r = 5.0 cm), (b) point b (r = 0), and (c) point c (r = 5.0 cm)?
View Solution
Knowledge Check
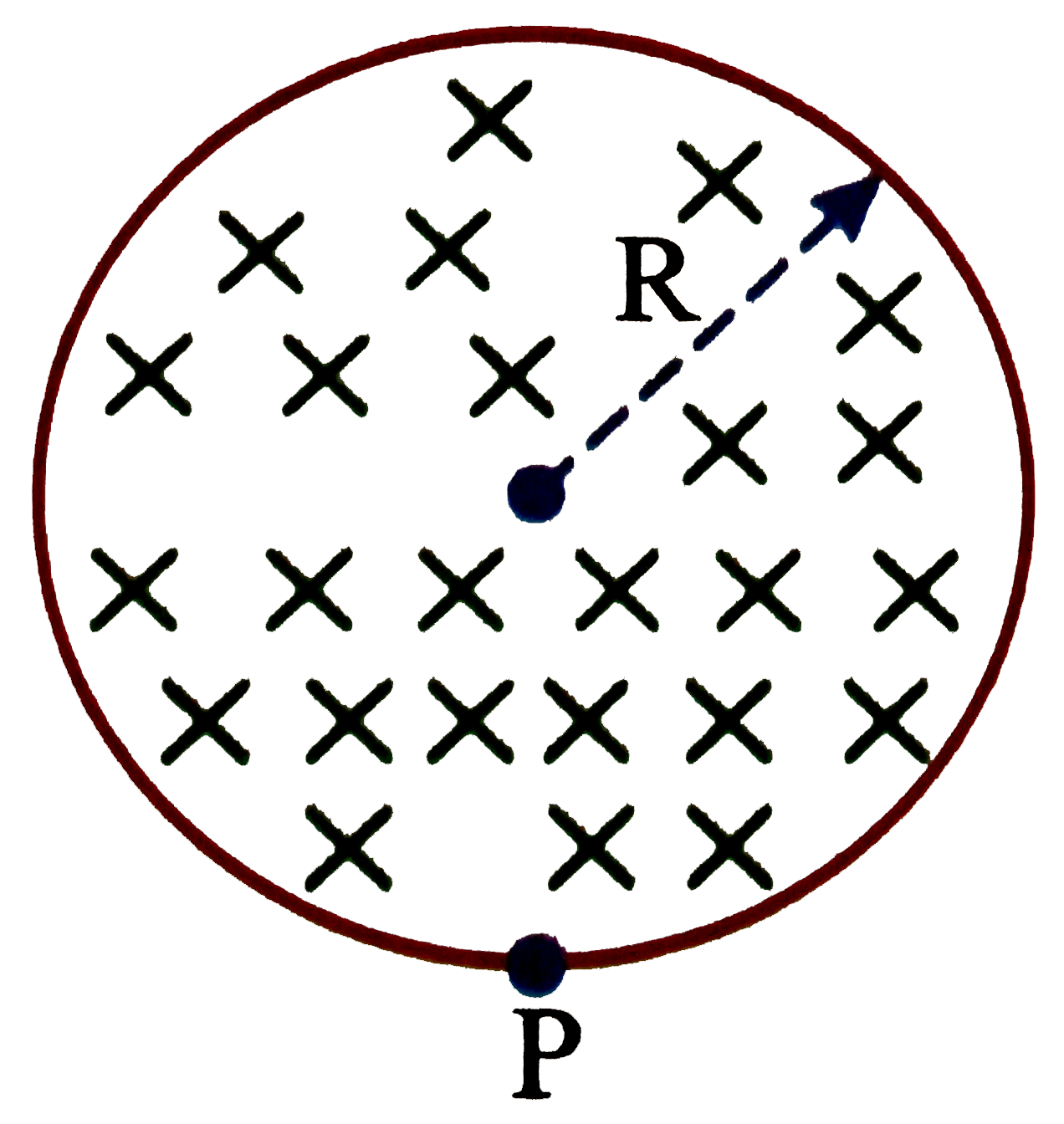
Figure shown a uniform magnetic field B confined to a cylindrical volume and is increasing at a constant rate. The instantaneous acceleration experienced by an electron placed at P is
 Azero, since charge on electron in constantBtowards rightCtowards leftDupwords
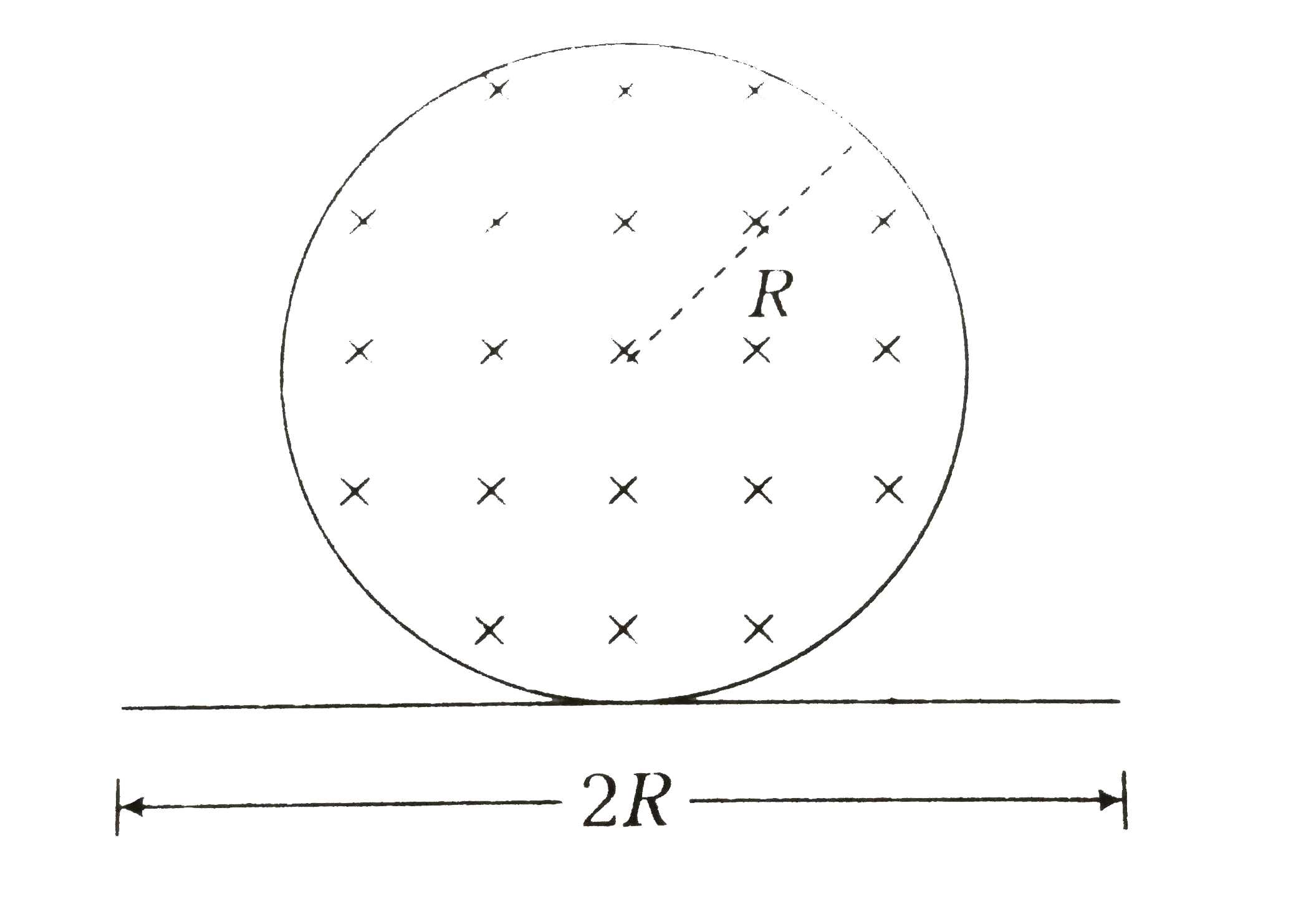
Azero, since charge on electron in constantBtowards rightCtowards leftDupwordsA uniform magnetic field of induction B is confined to a cyclindrical region of radius R. The magnetic field is increasing at a constant rate of dB/dt (tesla/ second). A charge q of mass m, placed at the point P on the periphery of the fixed experiences an acceleration :
 A12eRmdBdt towards leftB12eRmdBdt towards rightCeRmdBdt towards leftDzero
A12eRmdBdt towards leftB12eRmdBdt towards rightCeRmdBdt towards leftDzeroA uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure.
The magnitude of induced emf across the rod isAπR2αBπR2α2CR2α√2Dπr2α4
A uniform magentic field of induction B is confined in a cyclinderical region of radius R. If the field is incresing at a constant rate of dBdt=αT/s, then the intensity of the electric field induced at point P, distant r from the axis as shown in the figure is proportional to :
View SolutionA uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure.

The magnitude of induced emf across the rod is
View SolutionA uniform magnetic field of induction B is confined to a cyclindrical region of radius R. The magnetic field is increasing at a constant rate of dB/dt (tesla/ second). A charge e of mass m, placed at the point P on the periphery of the fixed experiences an acceleration :

View SolutionA uniform magnetic field B=B0t (where B0 is a positive constant) fills a cylindrical volume of radius R then the potential difference in the conducting rod PQ due to electrostatic field is :
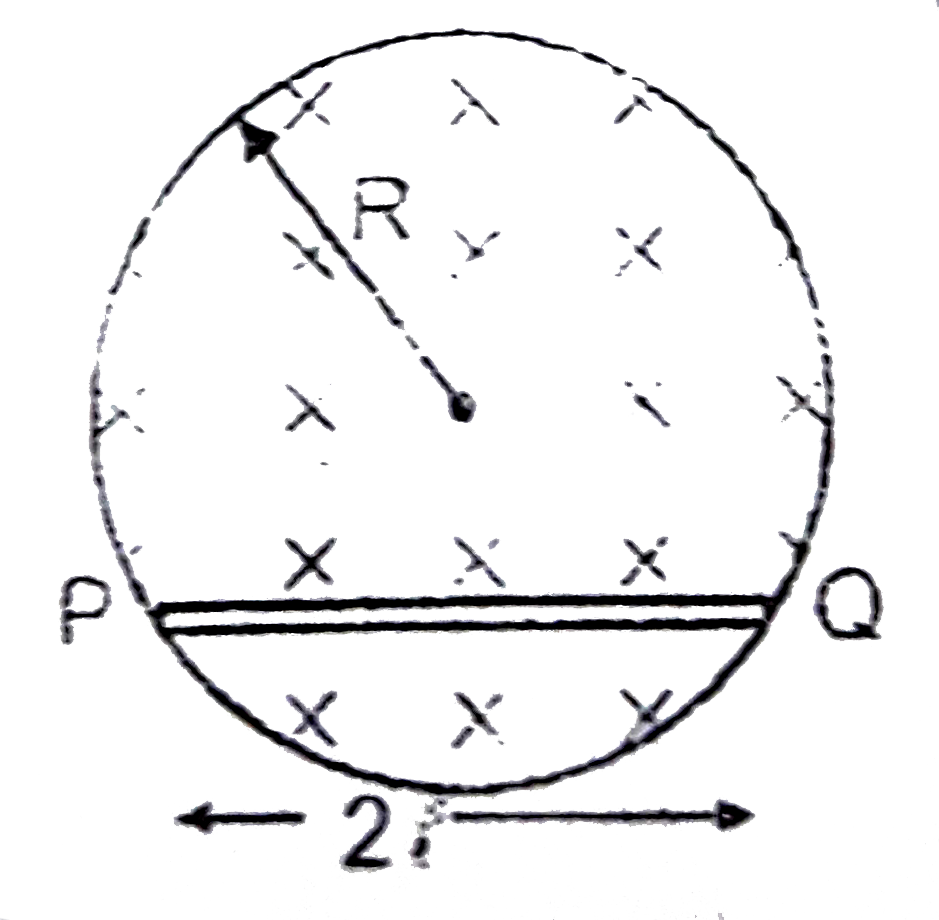
View Solutiona uniform magnetic field of induction B fills a cylinderical volume of radius R. A rod AB of length 2l is placed as shown in . If B changing at the rate dB/dt, the emf that is produced by the changing magnetic field and that acts between the ends of the rod is
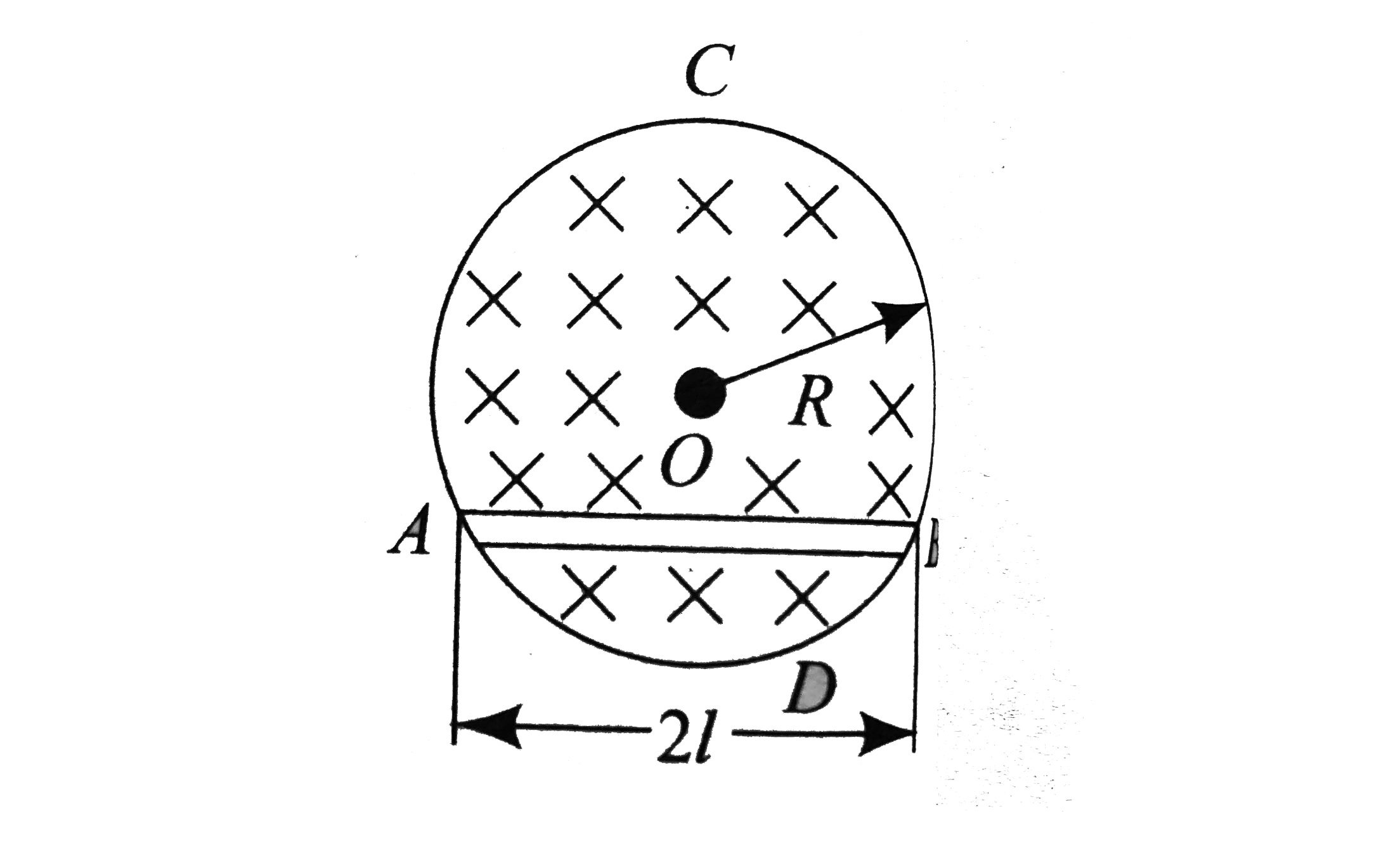
View Solution
