Find :
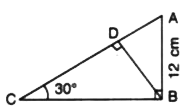
(i) BC
For (a) 
¯¯¯¯¯B1=μ04πir,¯¯¯B2=12μ02ir=μ0i4r⊙
¯¯¯B3=μ04πir=μ0i4πr⊙,¯¯¯Bp=B1+B2+B3
¯¯¯Bp=μ04πir+μ0i4r⊙+μ04πir⊙,¯¯¯Bp=μ0i4r⊙
For (b) 
¯¯¯B1=¯¯¯B3=0,¯¯¯B2=12μ0i2r=μ0i4r
For (c) 
¯¯¯B1=0,¯¯¯B2=34μ0i2r=3μ0i8r,¯¯¯B3=μ0i4πr⊙
¯¯¯Bp=34μ0i2r+μ0i4πr⊙=μ04ir(32−1π)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA
142 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
In the given figure, ABCD is a trapezium with angle C=120∘,DC=28 cm and BC=40 cm. Find :
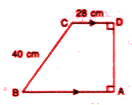
(i) AB
View SolutionThe vertices of a ΔABC are A (3, 8), B (-1, 2) and C (6, -6). Find :
(i) Slope of BC.
View SolutionThe vertices of a ΔABC are A(3, 8), B(-1, 2) and C(6, 6). Find :
(i) Slope of BC.
(ii) Equation of a line perpendicular to BC and passing through A.
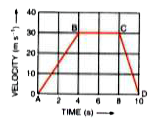
View SolutionThe velocity-time graph of a moving body is given below in Fig. 2.43.(i) the acceleration in parts AB, BC and CD. Find :
(ii) displacement in each part AB, BC, CD, and
(iii) total displacement.
View SolutionIf A=[1324],B=[1243]andC=[4312]. Find
(i) (AB) C (ii) A (BC)
Is A(BC)=(AB)C?
View SolutionIn the given figure, DE // BC and AE : EC = 5 : 4. Find :
DE : BC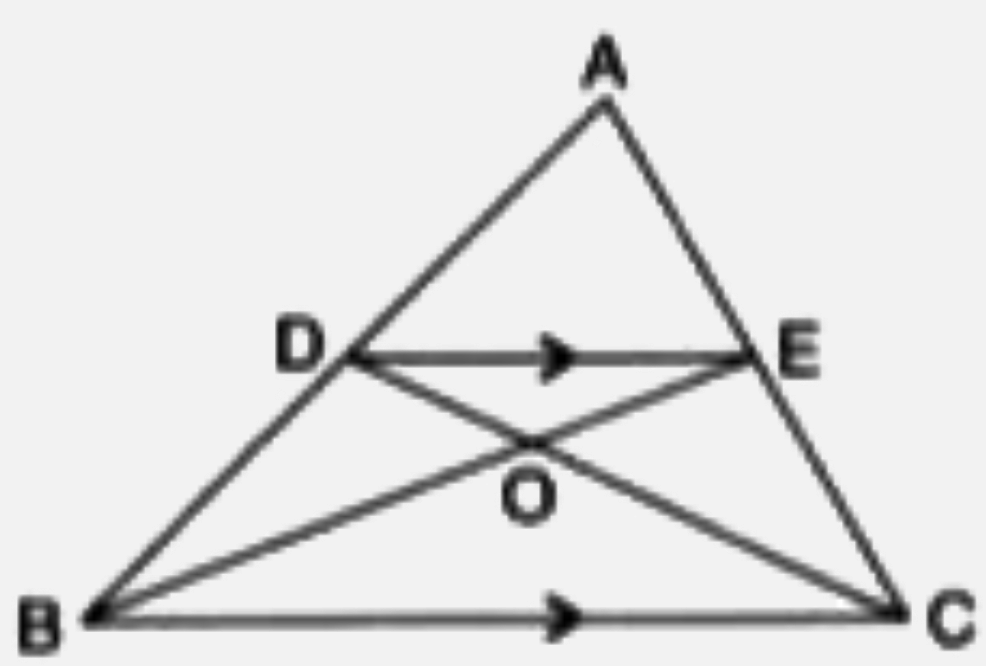
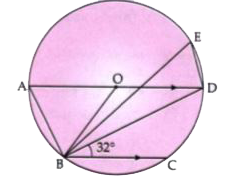
View SolutionIn the figure given below, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD=32∘. Find : (i) ∠OBD (ii) ∠AOB (iii) ∠BED
View SolutionIn trapezium ABCD, as shown, AB||DC, AD = DC = BC = 20 cm and ∠A=60∘ Find :
 (i) length of AB
(i) length of AB
(ii) distance between AB and DC
View SolutionIf a=10, b=4, c=6, d=9, find :-
(i)adbc
(ii)ad×bc
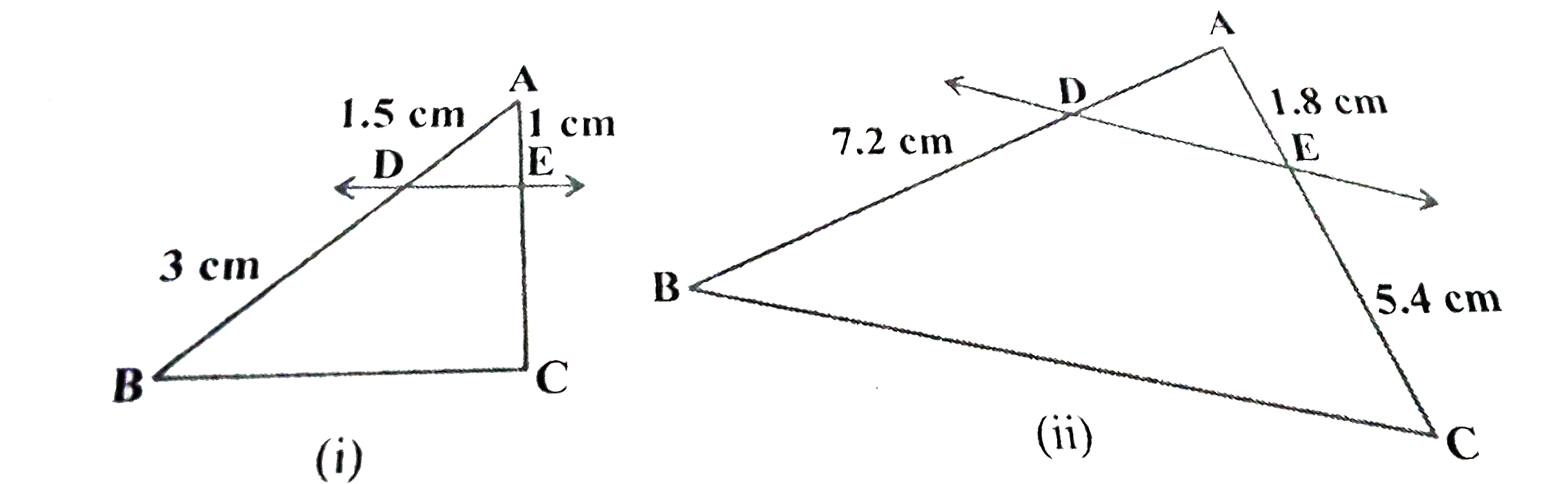
View SolutionIn Figure (i) and (ii), DE||BC. Find EC in (i) and AD in (ii).
View Solution
