If a=10, b=4, c=6, d=9, find :-
(i)adbc
(ii)ad×bc
The correct Answer is:(i)154
(ii) 2160
Step by step video & image solution for If a=10, b=4, c=6, d=9, find :- (i)(ad)/(bc) (ii)ad xx bc by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (VECTORS)
60 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Units, Dimensions & Measurements)
30 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Graphs))
29 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Find :
(i) BC
(ii) AD
(iii) AC
View SolutionIn a △ABC , AD is the bisector of ∠A , meeting side BC at D . (i)IfAB=10cm , AC=14cm and BC=6cm , find BD and DC (ii)IfAC=4.2cm , DC=6cm and BC=10cm , find AB . (iii)IfAB=5.6cm , AC=6cm and DC=3cm , find BC .
View SolutionIf the four consecutive coefficients in any binomial expansion be a, b, c, d, then prove that (i) a+ba,b+cb,c+dc are in H.P. (ii) (bc+ad)(b−c)=2(ac2−b2d)
View SolutionIf the four consecutive coefficients in any binomial expansion be a, b, c, d, then prove that (i) a+ba,b+cb,c+dc are in H.P. (ii) (bc+ad)(b−c)=2(ac2−b2d)
View SolutionProve that the points (a, b), (c, d) and (a-c, b-d) are collinear, if ad = bc.
View SolutionIf the roots of Quadratic i2x2+5ix−6 are a+ib and c+ (a,b,c,d∈R and i=√−1) then, (ac−bd)+(ad+bc)i=?
View Solutiona, b, c, d are integers such that ad + bc divides each of a, b, c and d.Prove that ad+bc=±1
View SolutionIn the figure chords AE and BC intersect each other at point D
(i) If ∠CDE=90∘
AB=5cm
BD=4cm and CD=9 cm
find DE
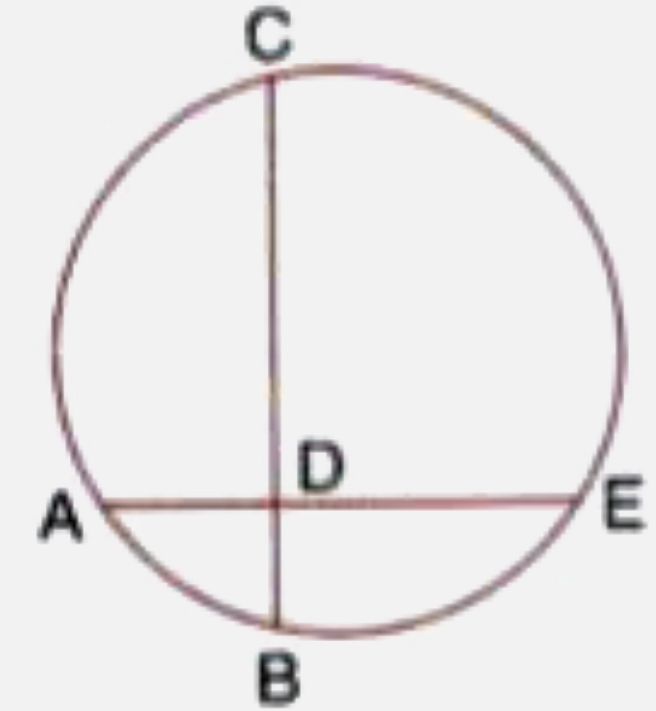
(ii) If AD=BD, show that AE=BC
View SolutionIf A=[1324],B=[1243]andC=[4312]. Find
(i) (AB) C (ii) A (BC)
Is A(BC)=(AB)C?
View SolutionThe vertices of a ΔABC are A(3, 8), B(-1, 2) and C(6, 6). Find :
(i) Slope of BC.
(ii) Equation of a line perpendicular to BC and passing through A.
View Solution
