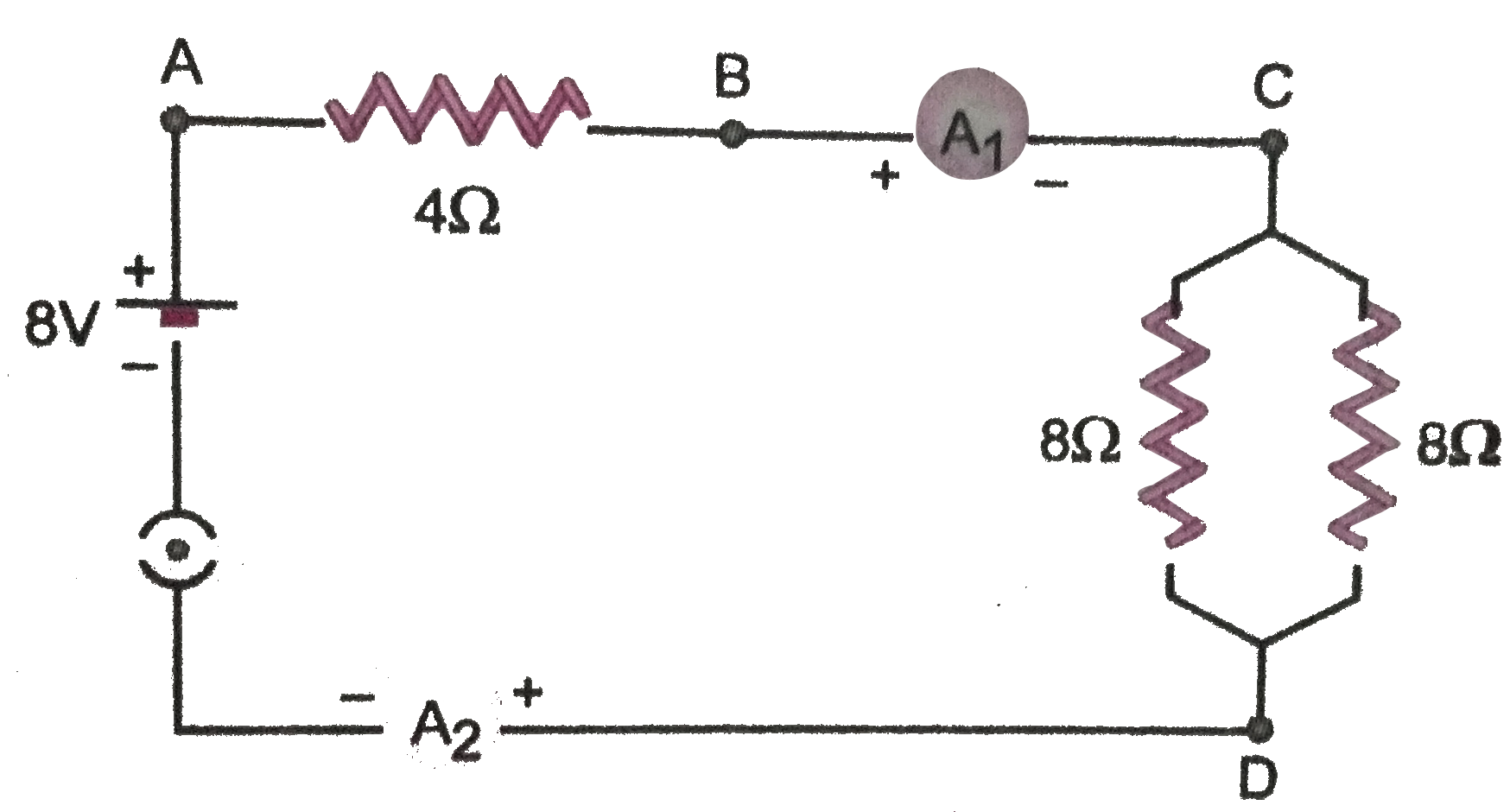
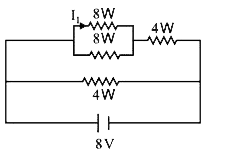
Find out the folowing in the electric circuit given in (Fig. 3.48).
(a) Effective resistance of two 8Ω resistors in the combination
(b) Current flowing through 4Ω resistor
( c) Potential difference across 4Ω resistance
(d) Power dissipated in 4Ω resistor
(e) Difference in ammeter readings, if any.
 .
.
Video Solution
Text Solution
(a) Since, two 8Ω resistors are in parallel, then their effective resistance RP is given by
1Rp=1R1+1R2
1Rp=18+18=14Ω
(b) Total resistance in the circuit R=4Ω+Rp
=4Ω+4Ω
=8Ω
Current through the circuit I=VR=88=1A
(where,V= Voltage of battery andR=Net equivalent resistance of circuit)
Thus, current through 4Ω resistor is 1 A as 4Ω and Rp are in series and same current flows through them.
(c) Potential difference across 4Ω resistor is potential drop by the 4Ω resistor i.e, V=IR=1×4=4V
(d) Power dissipated in 4Ω resistor P=I2R=12×4=4W
(e) There is no difference in the readings of ammeters A1 and A2 as same current flows through all elements in a series current.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A current of 3A flows through the 2Ω resistor as shown in the circuit. The power dissipated in the 5Ω resistor is
 A5 watt.B4 watt.C2 watt.D1 watt
A5 watt.B4 watt.C2 watt.D1 watt
An alternating current of rms value 10 A is passed through a 12Ω resistor. The maximum potential difference across the resistor is
View SolutionIf the power dissipated in the 27Ω resistor in the circuit shown is 108 watt, the potential difference across the 4Ω resistor is
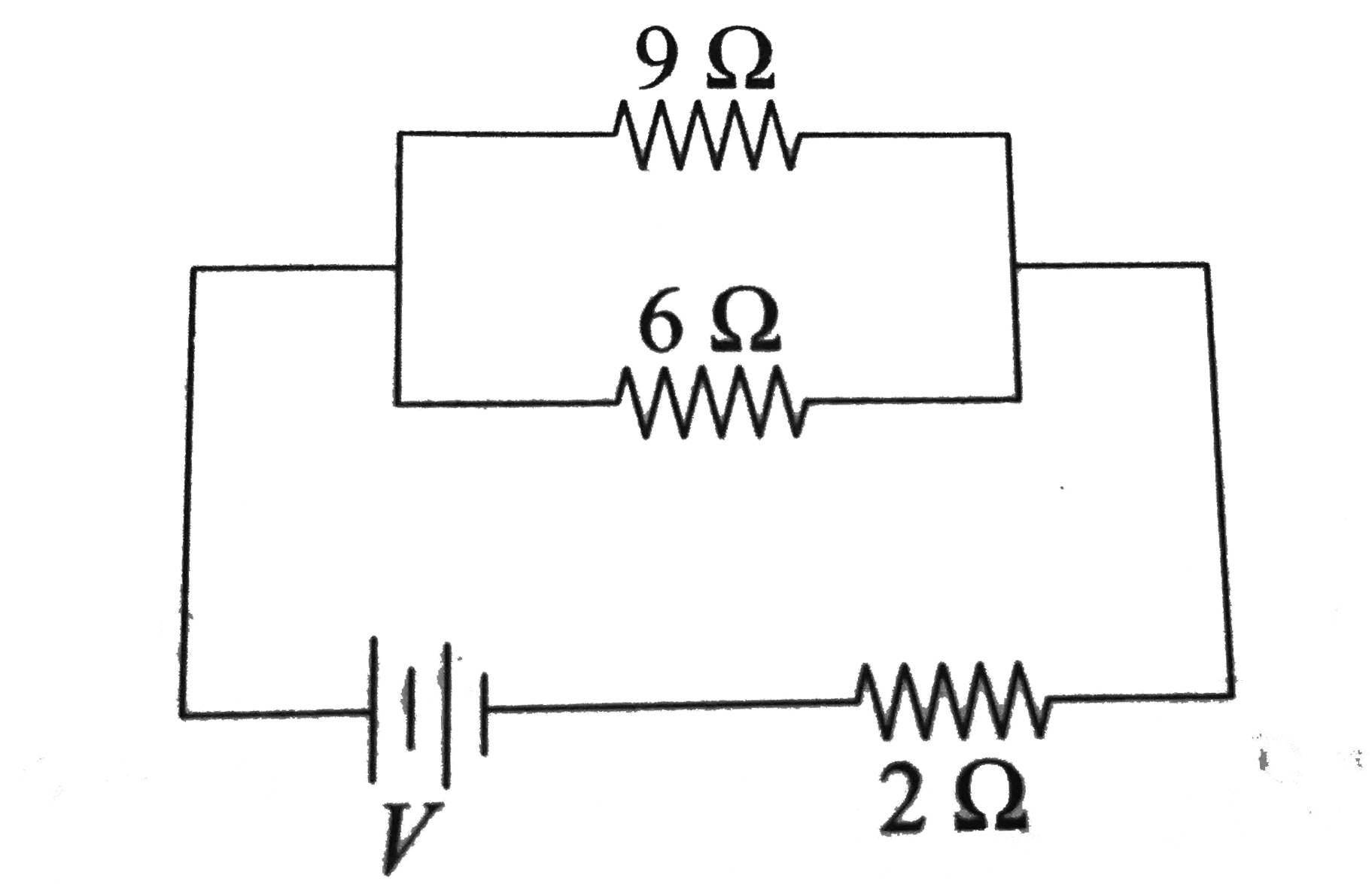
View SolutionIf power dissipated in the 9Ω resistor in the resistor shown is 36W, the potential difference across the 2Ω resistor is
 View Solution
View SolutionThe current I1 (in A) flowing through 3Ω resistor in the following circuit is:
 View Solution
View SolutionFind the current through 4Ω resistor in the circuit shown in figure.
 View Solution
View SolutionIn the following circuit, 18Ω resistor develops 2J/sec due to current flowing through it. The power developed across 10Ω resistance is
 View Solution
View SolutionThe current I1 (in A) folowing through 8Ω resistor in the following circuit is:
 View Solution
View Solution