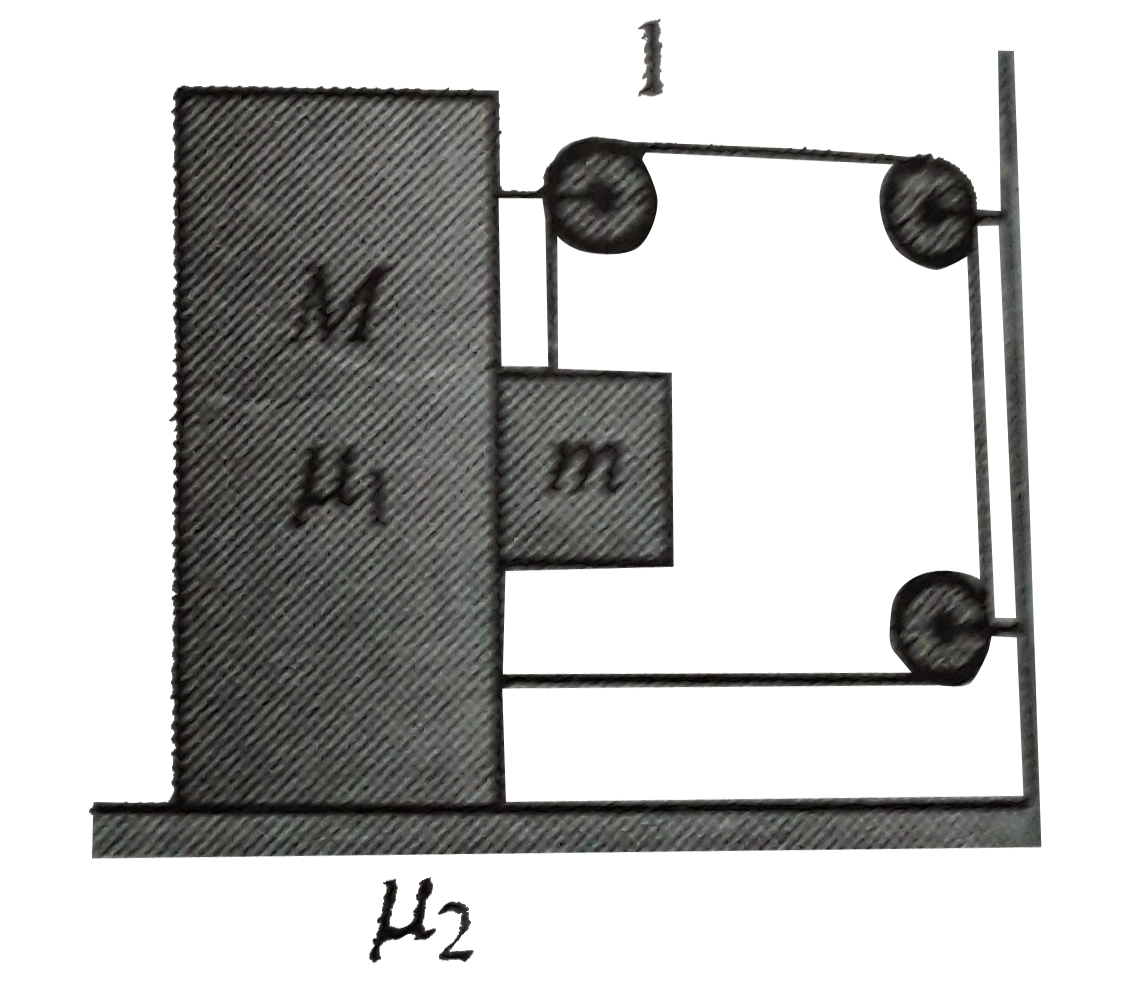
Find the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is $μ_{1}$ and that between the bigger block and the ground is $μ_{2}$ .

Text Solution

Verified by Experts

The correct Answer is:A, B

Let the acceleration of the block M is a towards rilght. So the block m must to down with an acceleration 2a.
M it will also have acceleration a towards right. So it will experience two nertial forces as shown the free body diagram. From free body digram........1

$R_{1} - m a = 0$
$\to R_{1} = m a$ ..........i
Again, $2 m a + T - M g + μ_{1} R_{1} = 0$
$\to T = M g - (2 + μ_{1}) m a$ .........ii
From free body diagram -2,
$T + μ_{1} R_{1} + M g - R_{2} = 0$
Putting the value of $R_{1}$ from i
$R_{2} = T + μ_{1} m a + m g$
Putting teh value of T from ii,
$R_{2} = (M g - 2 m a - μ_{1} m a) = μ_{1} m a + M g + m g$
R_2=Mg+mg-2ma $... . . i i i < b r > A g a \in o m n t h e e e b o d y d i a g r a m 2, < b r >$ T+T-R-Ma-mu_2R_2=0 $< b r >$ rarr 2T-Ma-ma-mu_2(Mg+mg-2ma)=0 $< b r > P u \in g t h e v a l u e s o f$ R_1 and R_2 $o m i and i i i < b r >$ 2T=(M+m)a+mu_2(Mg+mg-2ma) $... . i v < b r > F r o m e q u a t i o n i i and i v w e h a v e < b r >$ 2T=2mg-2(2+mu_1)ma $< b r >$ =(M+m)a+mu_2(Mg+mg-2ma) $< b r >$ rarr 2mg-mu_2(M+m)g $< b r >$ =a[M+m-2mu_2m+4m+2mu_1m] $< b r >$ rarr a=([2m-m_2(M+m)]g)/(M+m[5+2(mu_1-mu_2)])

|

Updated on:21/07/2023

Class 11 PHYSICS FRICTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A block of mass $m$ is placed on another block of mass $M$ which itself is lying on a horizontal surface .The coefficient of friction between two blocks is $μ_{1}$ and that between the block of mass $M$ and horizontal surfece is $μ_{2}$ What maximum horizontal force can be applied to the lower block move without separation?

A $(M + m) (μ_{2} - μ_{1}) g$
B $(M - m) (μ_{2} - μ_{1}) g$
C $(M - m) (μ_{2} + μ_{1}) g$
D $(M + m) (μ_{2} + μ_{1}) g$
Question 2 - Select One
A block of mass $m_{2}$ is placed on a horizontal table and another block of mass $m_{1}$ is placed on top is it. An increasing horizontal force $F = α t$ is exerted on the upper block but the lowwer block never moves as a result. If the coefficient of friction between the blocks is $μ_{1}$ coefficient of friction between the blocks is $μ_{1}$ and that between the lower block and the table is $μ_{2},$ then what is the maximum possible value of $μ_{1} / μ_{2}$ ?
A $\frac{m_{2}}{m_{1}}$
B $1 + \frac{m_{2}}{m_{1}}$
C $\frac{m_{1}}{m_{2}}$
D $1 + \frac{m_{1}}{m_{2}}$

HC VERMA-FRICTION-Exercises

Home
Ask Doubt
Profile