Find the angular momentum of an oxygen molecule whose rational energy is E=2.16meV and the distance between the nuclei is d=121pm.
The angular momentum is √2E=M
Now I=md24(m=mass ofO2molecule)=1.9584×10−39gmc2
So M=3.68×10−27ergsec.=3.49ħ
(This corresponding to J=3)
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Radioactivity
35 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Nuclear Reaction
42 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom
69 Videos
- DIRECT CURRENTBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions
15 Videos
Similar Questions
Knowledge Check
The relation between angular momentum J of a body and rotational kinetic energy is given by J=√2EI. The graph between J and √E will be:
A B
B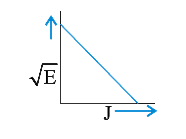 C
C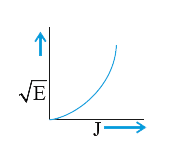 D
D
A neutron of energy 1 MeV and mass 1.6×10−27 kg passes a proton at such a distance that the angular momentum of the neutron relative to the proton approximately equals 10−33Js. The distance of closest approach neglecting the interaction between particles si
A0.44nmB0.44mmC0.44ÅD0.44fm
Find the number of ratational levels per unit energy interval, dN/dE, for a diatomic molecule as a function of rotational energy E. Calculate of an magnitude for an iodine molecule in the state with rotational quantum number J=10. The distance between the nuclei of that molecule is equal to 267pm.
View SolutionCalculate the angular momentum of a body whose rotational energy is 10 joule. If the angular momentum vector coincides with the axis of rotation and its moment of inertia about this axis is 8×10−7 kg m^(2)
View SolutionFind the centre of mass of the water molecule. Given that the m0=16mH the distance between the oxygen atoms and hydrogen atom is 1.02° A and (the angle made by .the two hydrogen atoms with the oxygen atom is 105∘
View SolutionThe relation between angular momentum J of a body and rotational kinetic energy is given by J=√2EI. The graph between J and √E will be:
View SolutionIf J is the angular momentum and E is the kinetic energy, then J2E has the dimensions of
View SolutionA neutron of energy 1 MeV and mass 1.6×10−27 kg passes a proton at such a distance that the angular momentum of the neutron relative to the proton approximately equals 10−33Js. The distance of closest approach neglecting the interaction between particles is
View Solution
