Derive Eq. (6.4c), making use of the Boltzmann distribution. From Eq.(6.4c) obtain the expression for molar vibration heat capacity CV vib of diatomic gas. Calculate CV vib for cl2 gas at the temperature 300K. The natural vibration frequency of these molecules is equal to 1,064.1014s−1.
by defination
<E>=ΣEVe−Ev/kTΣexp(−Ev/kT)=∂∂βΣ∞v=0eβEvΣ∞v=0e−βEv
=−∂∂βInΣ∞v=0e−β(v+1/2)ħω,β=1KT
=−∂∂βIne−1/2βħω11−e−βħω
=∂∂β[−12ħωβ−In(1−e−βħonrga)]
12ħω+ħωeħoega/kT−1
Thus for one gm mole of diatomic gas
Cv vib=N∂<E>∂T=R(ħωKT)2eħω/kT(eħω/kT−1)2
where R=Nk is the gas constant.
In the present case ħωKT=2.7088
and CV 1 vib=0.56R
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Radioactivity35videos
ATOMIC AND NUCLEAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Nuclear Reaction42videos
ATOMIC AND NUCLEAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom69videos
ATOMIC AND NUCLEAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions15videos
DIRECT CURRENT
Similar Questions
Find the ratio of intensities of the voilet and red satellites closest to the fixed line, in the vibraiton sopecturm of Raman scattering by Cl2 molecule at a temperature T=300K if the natural Vibration frequency of these molecules is ω=1.06.1014s−1,. By what factor will this ratio change if the temperature is doubled?
View SolutionWhich of the following is true for the molar heat capacity of an ideal gas?
1.It cannot be negative
2.It has only two values (CPandCV)
3.It can have any value
4.It cannot be zeroView Solution
Knowledge Check
- Question 1 - Select One
The ratio of specific heats of a gas is 1.4. if the value of CV is 20.8 J/mol K, then the CP is
A3.93 cal/mol KB4.93 cal/mol KC5.93 cal/mol KD6.93 cal/mol K - Question 2 - Select One
For a gas molecule with 6 degrees of freedom, the law of equipartition of energy gives the relation between the molar specific heat (CV) and gas constant (R ) is
ACV=R2BCV=RCCV=2RDCV=3R - Question 3 - Select One
Heat capacity (CV) of an ideal gas is X KJ/mole/K. To rise its temperature from 298 K to 318 K, heat to be supplied per 10g gas will be (in KJ) [MW = 16]
A16XB6.25XC32XD12.5X
5.6dm3 of an unknown gas at S.T.P requires 52.25J of heat to raise its temperature by 10∘C at constant volume. Calculate CV,CP and atomicity of the gas
View SolutionThe ratio of the molar heat capacities of an ideal gas is (CpCv76). Calculate the change in internal energy of 1.0mole of the gas when its temperature is raised by 50k(a) keeping the pressure constant , (b) keeping the volume constant and (c ) adiabatically.
View SolutionFigure. 6.10 shows heat capacity of a crystal vs temperatue in terms of the Debye theory. Here Ccl is classical heat capacity Θ is the Debye temperature. Using this plot, find:
(a0 The Debye temperature for silver if at a temperature T=65K its molar heat capacity is equal to 15J(mol.K),
(b) the molar heat capacity of aluminum at T=80K if at T=250K it is equal to 22.4J(mol.K)
(c )the maximum vibration frequency for copper whose heat capacity at T=125K differs form the classical value by 25%.
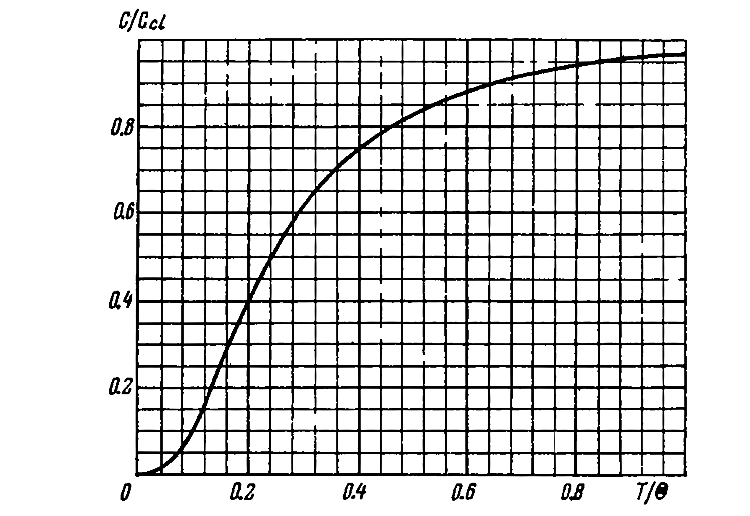 View Solution
View SolutionA certain gas is expanded from (1L, 10atm) to (4L, 5atm) against a constant external pressure of 1 atm. If the initial temperature of gas is 300K and heat capacity for the process is 50J∘C−1 (use 1L atm = 100J), then
View SolutionFor a gas molecule with 6 degrees of freedom the law of equipartition of energy gives the following relation between the molar specific heat (CV) and gas constant (R )
View Solution

