Find the appoximate formula expressing the mutual inductance of two thin coaxial loops of the same radius a if their centres are separated by a distance l, with l>>a
If a current I flows is one of the coils, the magnetic field at6 the centre of the other coil is,
B=μ0a2I2(l2+a2)3/2=μ0a2I2l3, as l>>a
The flux associated with the secound coil is then appoximately μ0πa4I/2l3
Hence, L12=μ0πa42l3
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field36videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics69videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
Knowledge Check
- Question 1 - Select One
The approximate formula expressing the formula of mutual inductance of two coaxial loops of the same redius a when their centers are separated by a distance l with l>>a is
A12μ0πa4l3B12μ0a4l2Cμ04ππa4l2Dμ0πa4l3 - Question 2 - Select One
What is the mutual inductance of a two-loop system as shown with centre separation l
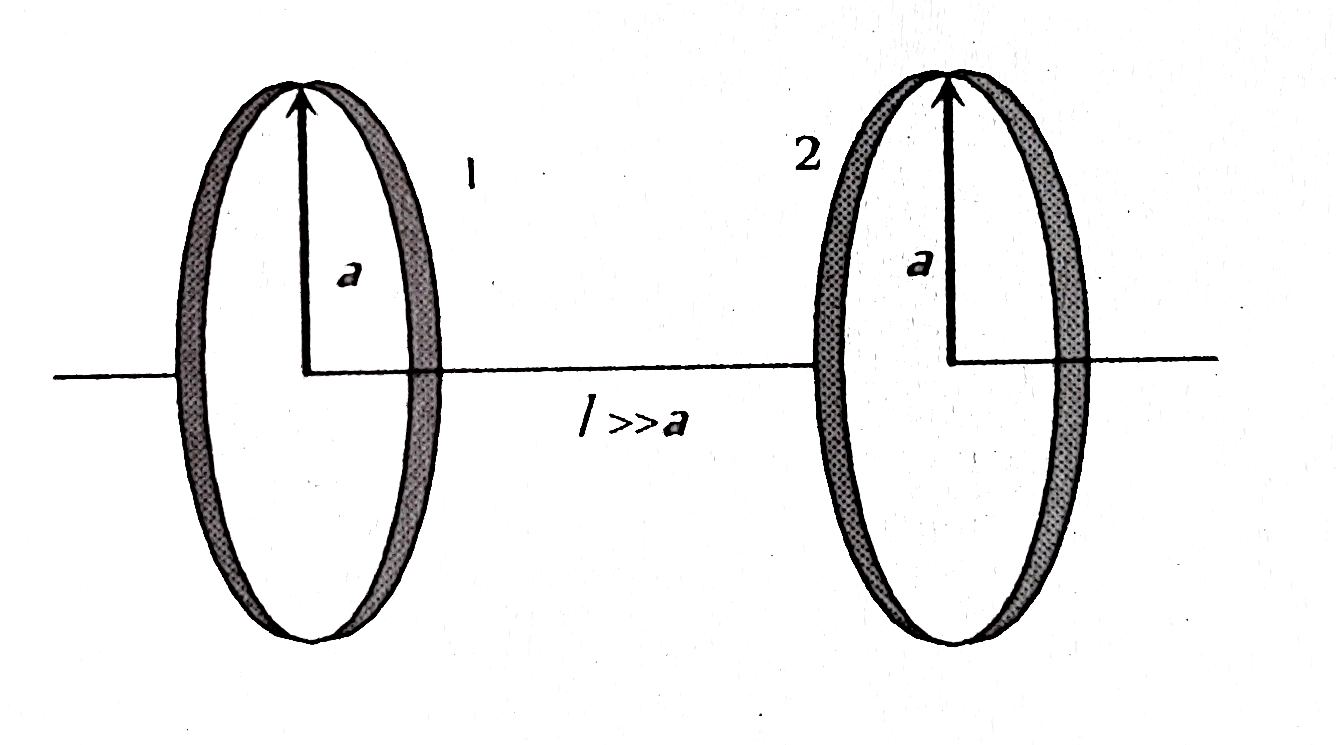 Aμ0πa48l3Bμ0πa44l3Cμ0πa46l3Dμ0πa42l3
Aμ0πa48l3Bμ0πa44l3Cμ0πa46l3Dμ0πa42l3 - Question 3 - Select One
Mutual inductance of two coils depends on their self inductance L1 and L2 as :
AM12=L1/L2BM12=L2/L1CM12=√L1L2DM12=√L1/L2
Obtain an expression for the self inductance of a straight solenoid of length l and radius r (l > > r).
View SolutionDetermine the capacitance of a system consisting of a metal ball of radius a and an infinite conducting plane separated from the centre of the ball by the distance l if l>>a.
View SolutionShow that if two inductors with equal inductance L are connected in parallel then the equivalent inductance of combination is L/2.The inductors are separated by a large distance.
View SolutionDefine the term 'mutual inductance between the two coils. Obtain the expression for mutual inductance of a pair of long coaxial solenoids each of length l and radii r1andr2(r2>r1). Total number of turns in two solenoids are N1andN2 respectively.
View SolutionWhat is the mutual inductance of a two-loop system as shown with centre separation l?
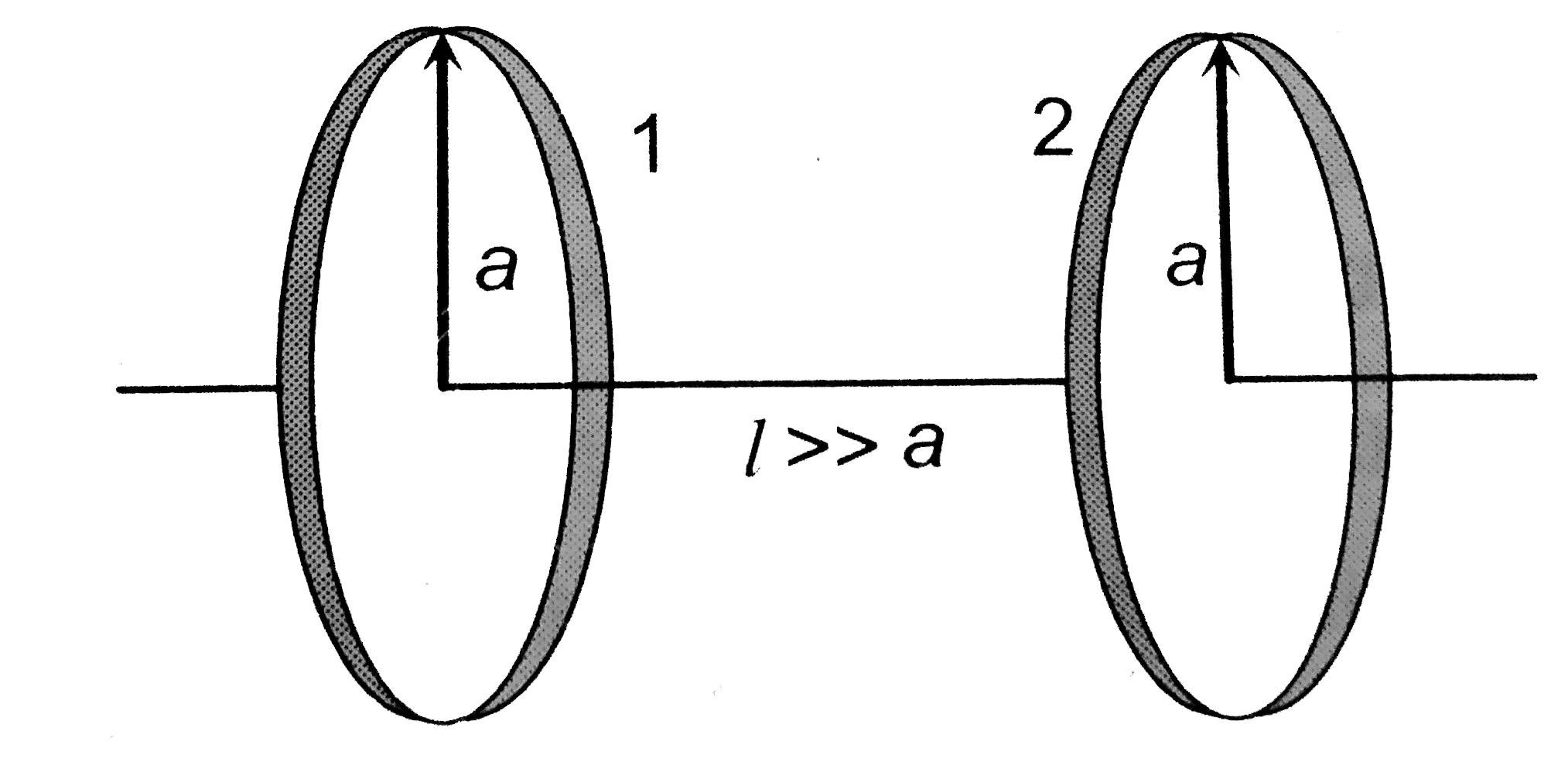 View Solution
View Solution