Find the centre of mass of a triangular lamina.
 Solution in Gujrati
Solution in Gujrati
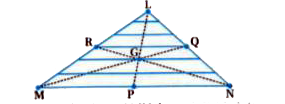
Suppose lamina be subdivided it into narrow strips each parallel to the base MN.
By symmetry each strip has its centre of mass at its midpoint. Joining the midpoint of all strips we get the median LP. The centre of mass of the triangle as a whole lie on the median LP. Similarly it lies on the medians, MQ and NR. Hence, the centre of mass lies on the point of concurrence of the medians, means on the centroid G of the triangle.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-B NUMERICALS FROM TEXTUAL EXERCISE
21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-B ADDITIONAL EXERCISE
12 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-A (TRY YOURSELF (VSQs))
94 Videos
- QUESTIONS ASKED IN JEE - 2020 BOOK - KUMAR PRAKASHANCHAPTER - QUESTIONS ASKED IN JEE - 2020 EXERCISE - Question
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - KUMAR PRAKASHANCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks
1 Videos
Similar Questions
Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body ?
View SolutionThe longest wavelength in Balmer series of hydrogen spectrum will be
View SolutionWhat is a rigid body ? Explain the differences between rigid body and solid body.
View SolutionA non-isotropic solid metal cube has coefficient of linear expansion as 5×10−5/∘C along the x-axis and 5×10−6/∘C along y-axis and z-axis. If the coefficient of volumetric expansion of the solid is n×10−6/∘C then the value of n is....
View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
View SolutionFind the centre of mass of a uniform triangula lamina.
View SolutionFind the centre of mass of a uniform L shaped lamina (a thin flat plate) with dimension as shown in Fig. The mass of the lamina is 3kg.

View SolutionLocate the centre of mass of uniform triangular lamina and a uniform cone.
View SolutionFind the position of centre of mass of the uniform lamina shown in figure. If the mass density of the lamina is sigma .
View SolutionFind the centre of mass of a uniform triangula lamina.
View SolutionLocate the centre of mass of a triangular lamina.
View SolutionFind the centre of mass of a triangular lamina.
View SolutionFind the centre of mass of a triangular lamina.
View SolutionFind the centre of mass of a triangular lamina.
View SolutionFind the centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 kg.
View Solution
