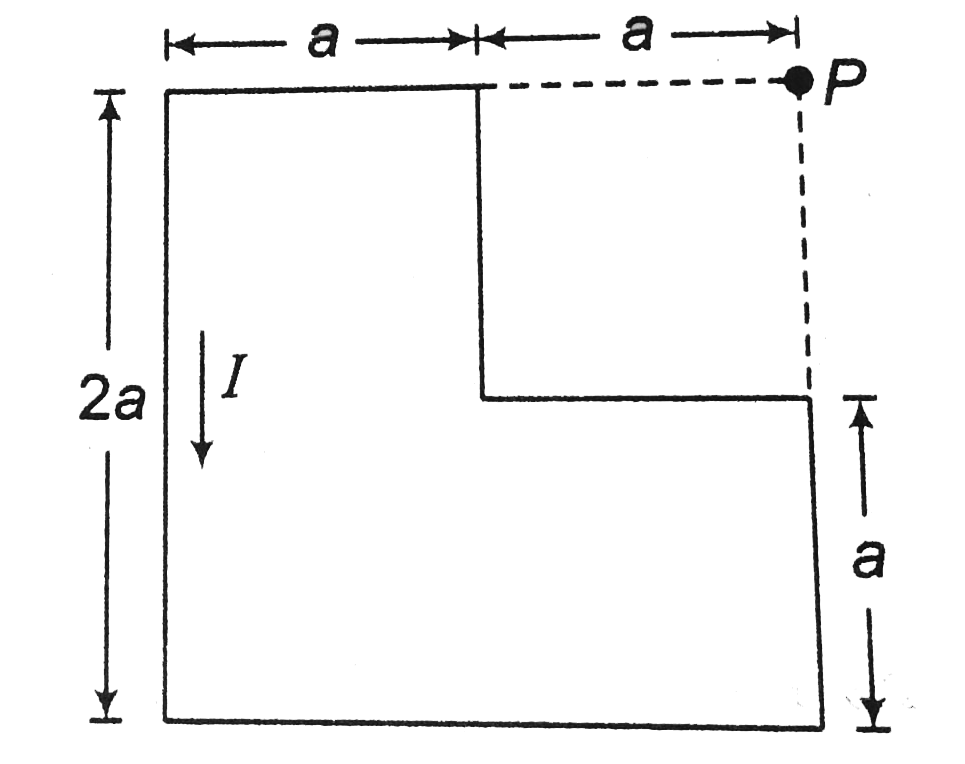
Find the emf across the points P and Q which are diametrically opposite points of a semicircular closed loop moving in a magnetic filed as shown in figure
 >
>
Induced emf = 2 Bav

Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IA58videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB18videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
Similar Questions
Find the emf across points P and Q which are diametrically opposite points of a semicircular closed loop moving in a magnetic field as shown in .
 View Solution
View SolutionFind the emf across points P and Q which are diametrically opposite points a semicircular closed loop moving in a magnetic field as shown in . Also draw the electrical equivalence od each branch.
 View Solution
View SolutionFind the emf across points P and Q which are diametrically opposite points a semicircular closed loop moving in a magnetic field as shown in . Also draw the electrical equivalence od each branch.
 View Solution
View SolutionFind the magnetic field B at the point P in figure
 View Solution
View SolutionFind the magnetic field at point O shown in the figure
 View Solution
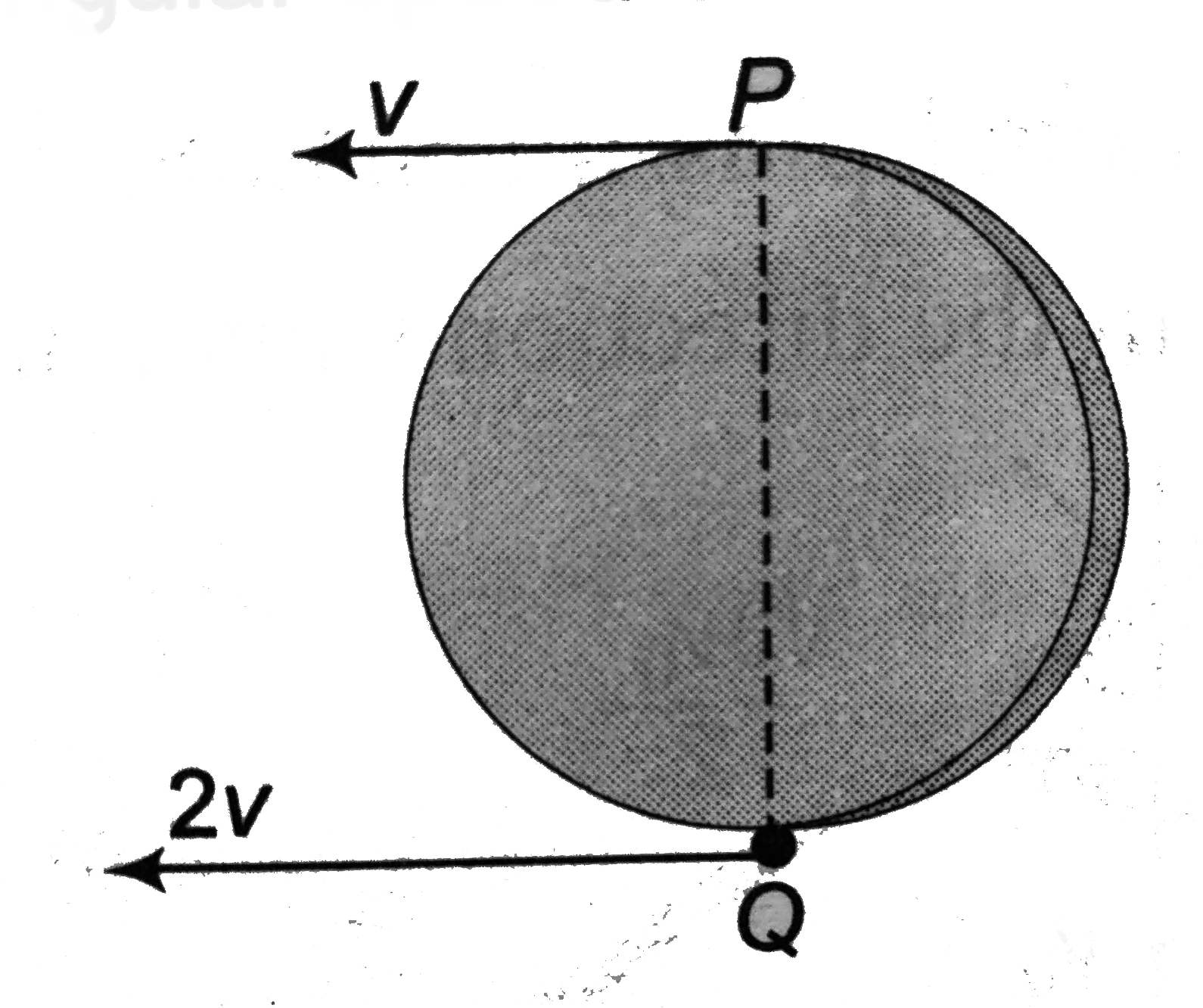
View SolutionTwo point P and Q. diametrically opposite on a disc of radius R have linear velocities v and 2v as shown in figure. Find the angular speed of the disc.
 View Solution
View SolutionThe net resistance between points P and Q in the circuit shown in figure is
 View Solution
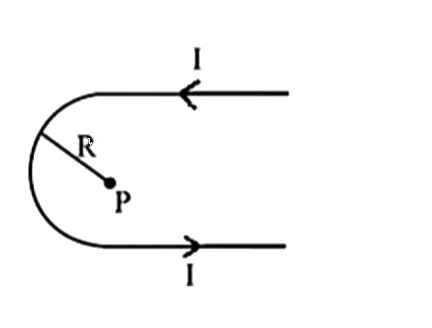
View SolutionWhat will be the magnetic field at point P in the figure below?
 View Solution
View SolutionWhich one is not correct for a cyclic process as shown in the figure ?
 View Solution
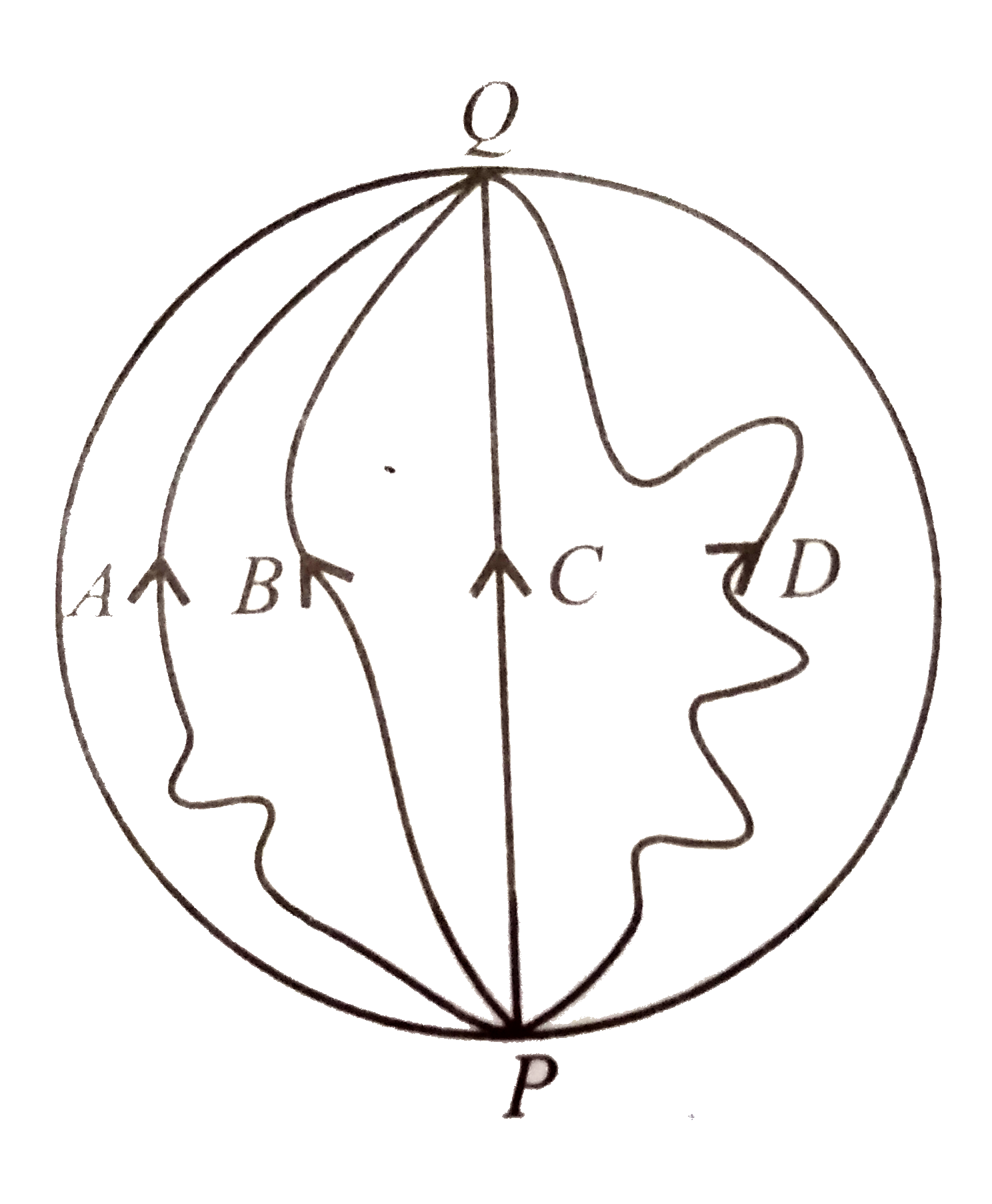
View SolutionFour girls skating on circular ice ground of radius 200 m start from a point P on the edge of the ground and reach a point Q diametrically opposite to P following different paths as shown in figure. For which girls displacement is equal to the actual length of path ?
 View Solution
View Solution

