Find the emf and the internal resistance of a source which is equivalent to two batteries connected in parallel whose emf's are equal to E1 and E2 and internal resistances to R1 and R2
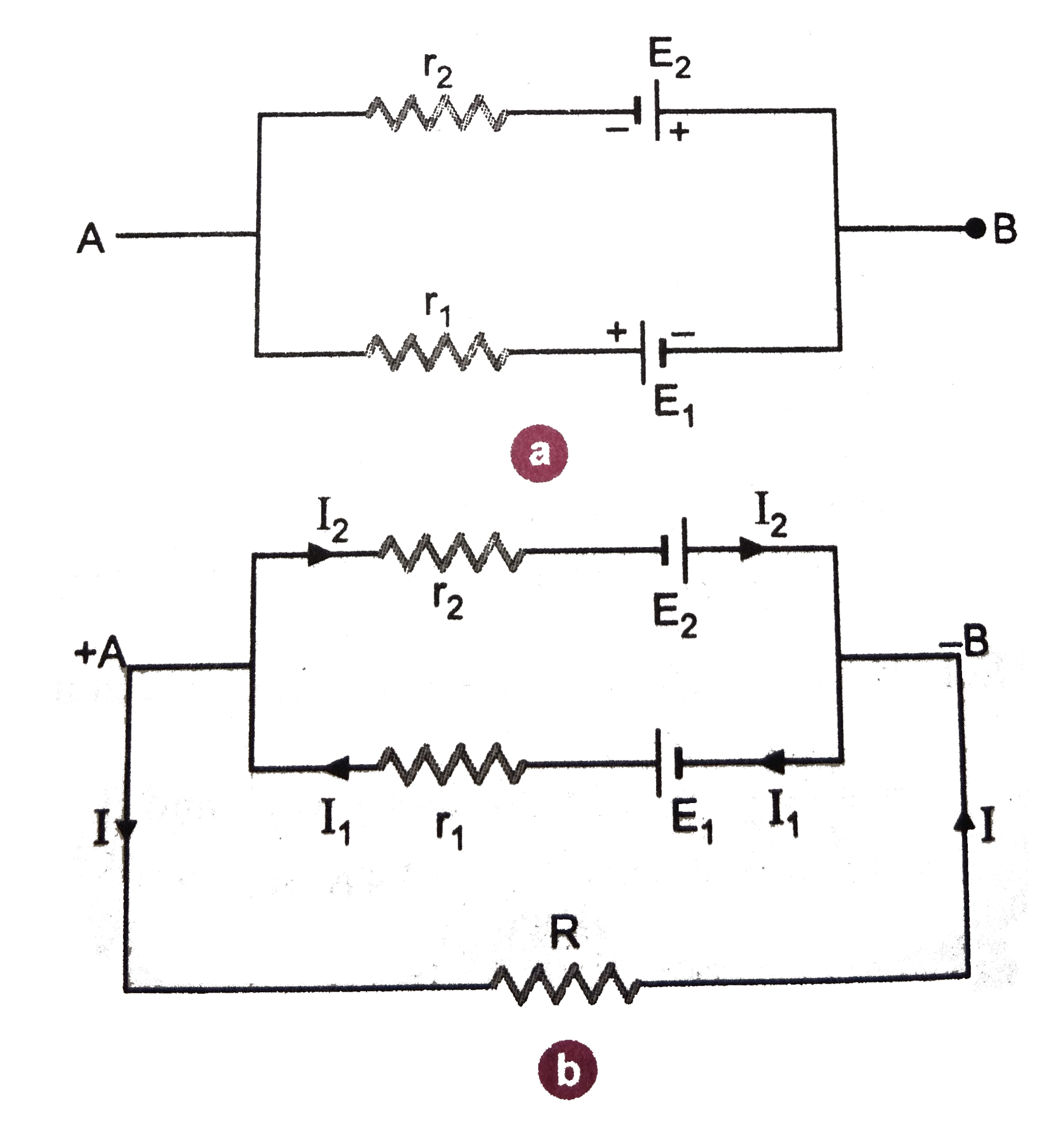
Let us connect a load of resistance R between the points A and B (fig)
From the loop rule, Δφ=0, we obtains
iR=ξ1−i1R1....(1)
and iR=ξ2−(i−i1)R2
or i(R+R2)=ξ+i1R2 ....(2)
Solving Eqs. (1) and (2), we get
i=ξ1R1+ξ2R2R1+R2/R+R1R2R1+R2=ξoR+R0 ....(3)
where ξ0=ξ1R1+ξ2R2R1+R2 and R0=R1R2R1+R2
Thus one can replace the given arrangement of the cells by a single cell having the emf ξ0 and internal resistance R0.

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics69videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction84videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field46videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
Find the emf ε and the internal resistance r of an electric source which is equivalent to two batteries of emf's ε1 and ε2 and internal resistances r1andr2, connected in parallel.
View SolutionFind the emf (V) and internal resistance (r) of a single battery which is equivalent to a parallel combination of two batteries of emf's V1,andV_(2), and internal resistance r1 and r2 respectively, with polarities as shown in the figure
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Six cell each of emf E and internal resistance r are connected in series. If due to over sight, two cells are connected wrongly, then the equivalent emf and internal resistance of the combination is
A6E,6rB4E,6rC2E,6rD2E,4r - Question 2 - Select One
If n cells each of emf E and internal resistance are connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr - Question 3 - Select One
Five cells each of emf E and internal resistance r are connected in series. Due to oversight one cell is connected wrongly . The equivalent emf and internal resistance of the combination is
A3E,3rB5E , 3rC3E, 5rD5E,5r
Find the e.m.f(E0) end internal resistance (r0) of a simple battery which is equivalent to a perallel combination of two battery of e.m.fE1andE2 and internal resistance v1andv2 respectively with polarities
 View Solution
View Solution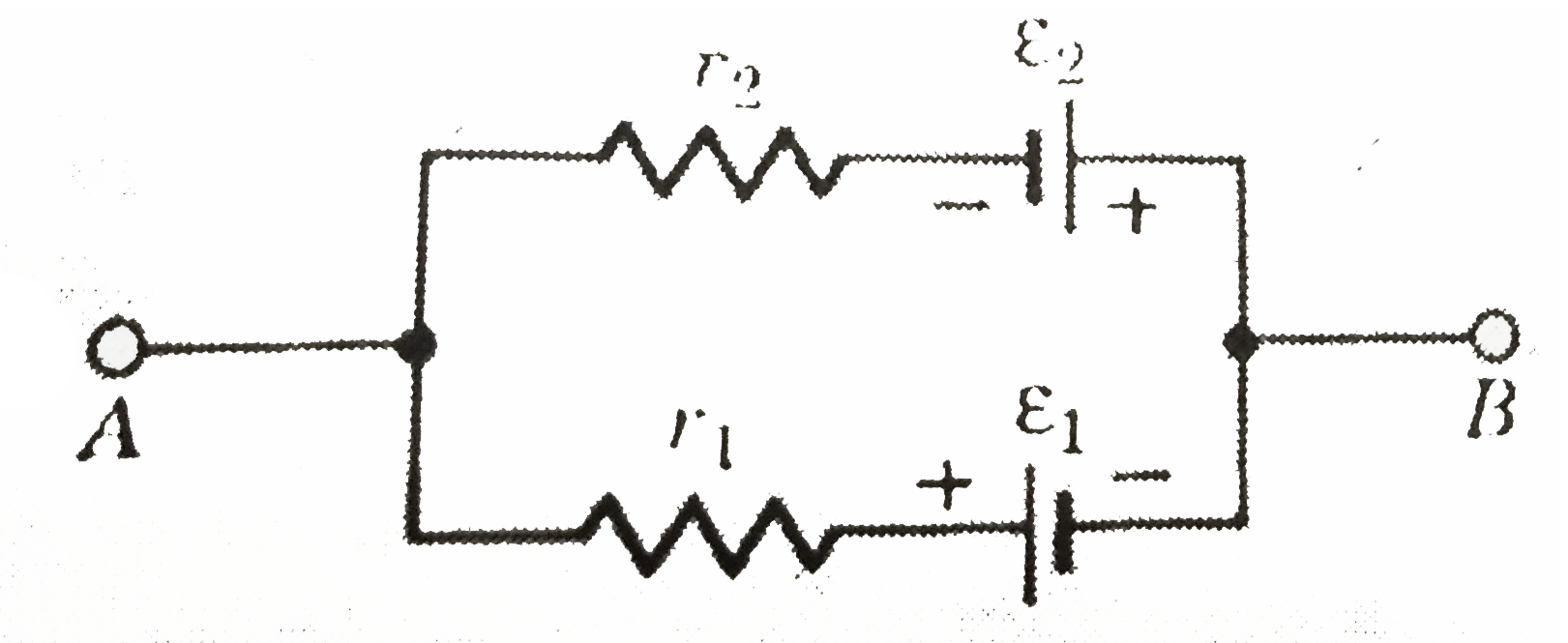
find the emf (ε0) and internal resistance (r0) if a battery which is equivalent to a parallel combination of two batteries of emfs ε1andε2 and internal resistances r1andr2 respectively, with polarities as shown in figure.View SolutionFind the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure
 View Solution
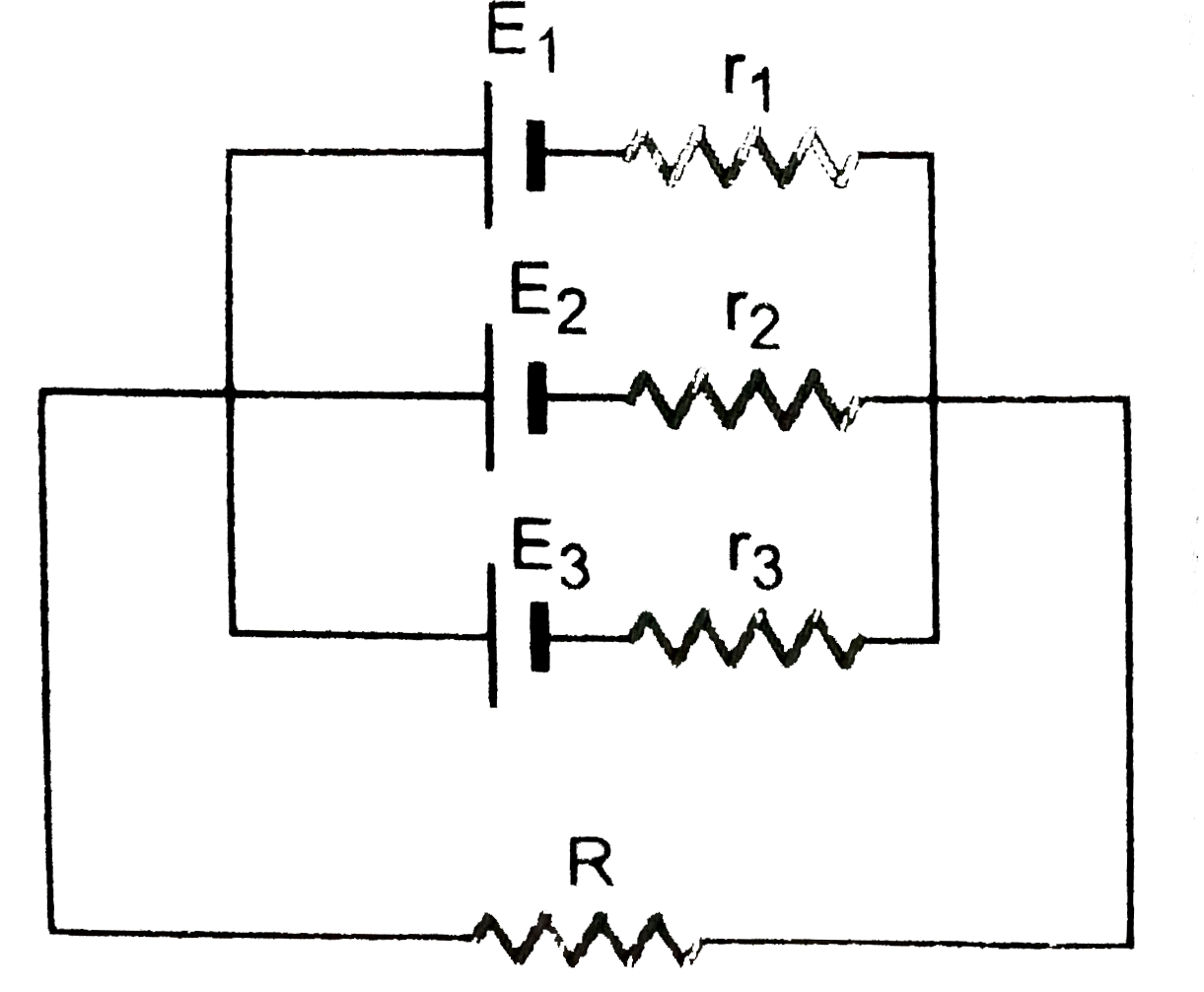
View SolutionIf three cell are connected in parallel then equivalent emf……. and equivalent internal resistance is …..
 View Solution
View SolutionTwo cells of emf 2ε and ε and internal resistance 2r and r respectively, are connected in parallel. Obtain the expressions for the equivalent emf and the internal resistance of the combination.
View Solution

