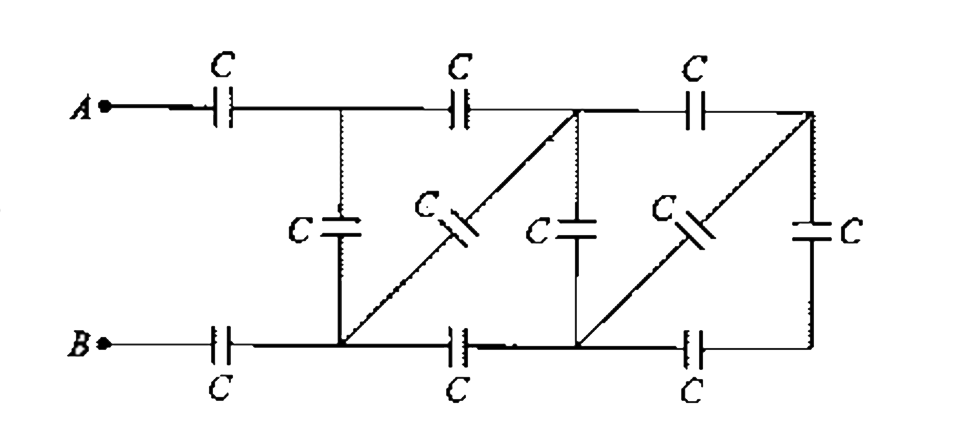
Find the equivalent capacitance of the network shown in the fig , when each capacitor is of 1 μF . When the ends X and Y are connected to a 6 V battery , find out (i) the charge and (ii) the energy stored in the network

The network may be redrawn as shown in fig
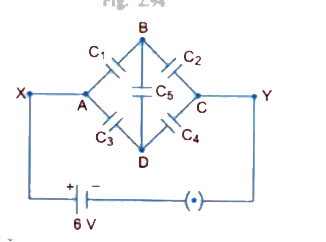
Here , C1=C2=C3=C4=C5=1μF As C1C2=C3C4 , hence the network is like a balanced wheatstone bridge where VB=VD , Hence capacitor C5 may be omitted from the circuit .
Now capacitance of series combination of C1 and C2 is C12=C1C2C1+C2=1×11+1=0.5μF
Similarly capacitance of series combination of C3 and C4 is C34=0.5μF
Since C12 and C34 are in parallel across points X and Y . hence the equivalent capacitance of the network C=C12+C34=0.5+0.5=1.0μF
(i) ∴ Net charge in the network Q = CV = (1.0μF)×(6V)=6.0μC
(ii) The energy stored in the network U=12QV=12×(6.0μC)×6V=18μJ
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - LONG ANSWER QUESTIONS-II
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST
1 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SHORT ANSWER QUESTIONS
48 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Videos
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
Knowledge Check
Find the total energy stored in capacitors in the network shown in Fig.
 A3.6 × 10 − 5 JB0.6 × 10 − 5 JC5.6 × 10 − 5 JDnone of these
A3.6 × 10 − 5 JB0.6 × 10 − 5 JC5.6 × 10 − 5 JDnone of these
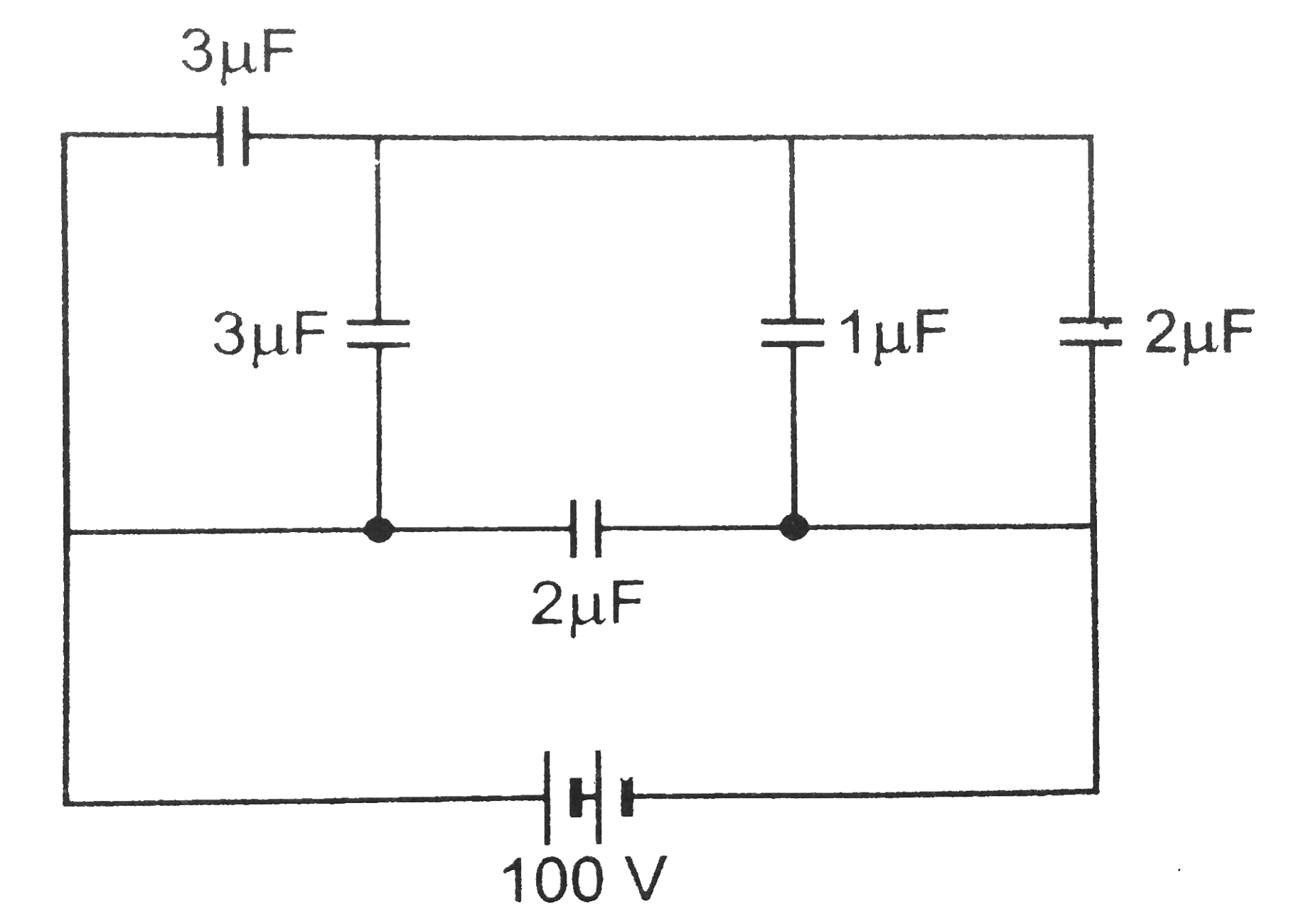
Fig, shows a network of five capacitors connected to a 100V supply. Calculate the total charge and energy stored in the network.
View SolutionA network of four 10μF capacitors is connected to a 500 V supply, as shown in Fig. Determine (a) the equivalent capacitance of the network and (b) the charge on each capacitor. (Note, the charge on a capacitor is the charge on the plate with higher potential, equal and opposite to the charge on the plate with lower potential.)

View SolutionA network of four 10μF capacitors is connected to a 500 V supply, as shown in Fig. Determine (a) the equivalent capacitance of the network and (b) the charge on each capacitor. (Note, the charge on a capacitor is the charge on the plate with higher potential, equal and opposite to the charge on the plate with lower potential.)

View Solution
(i) Find the equivalent capacitance of the combination shown in the figure (a), when C1=2.0μF,C2=4.0μFandC3=3.0μF
(ii) The input terminals A and B in Fig. (a) are connected to a battery of 12 V. Find the potential and the charge of each capacitor.
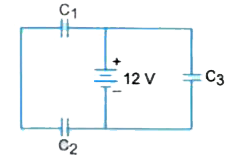
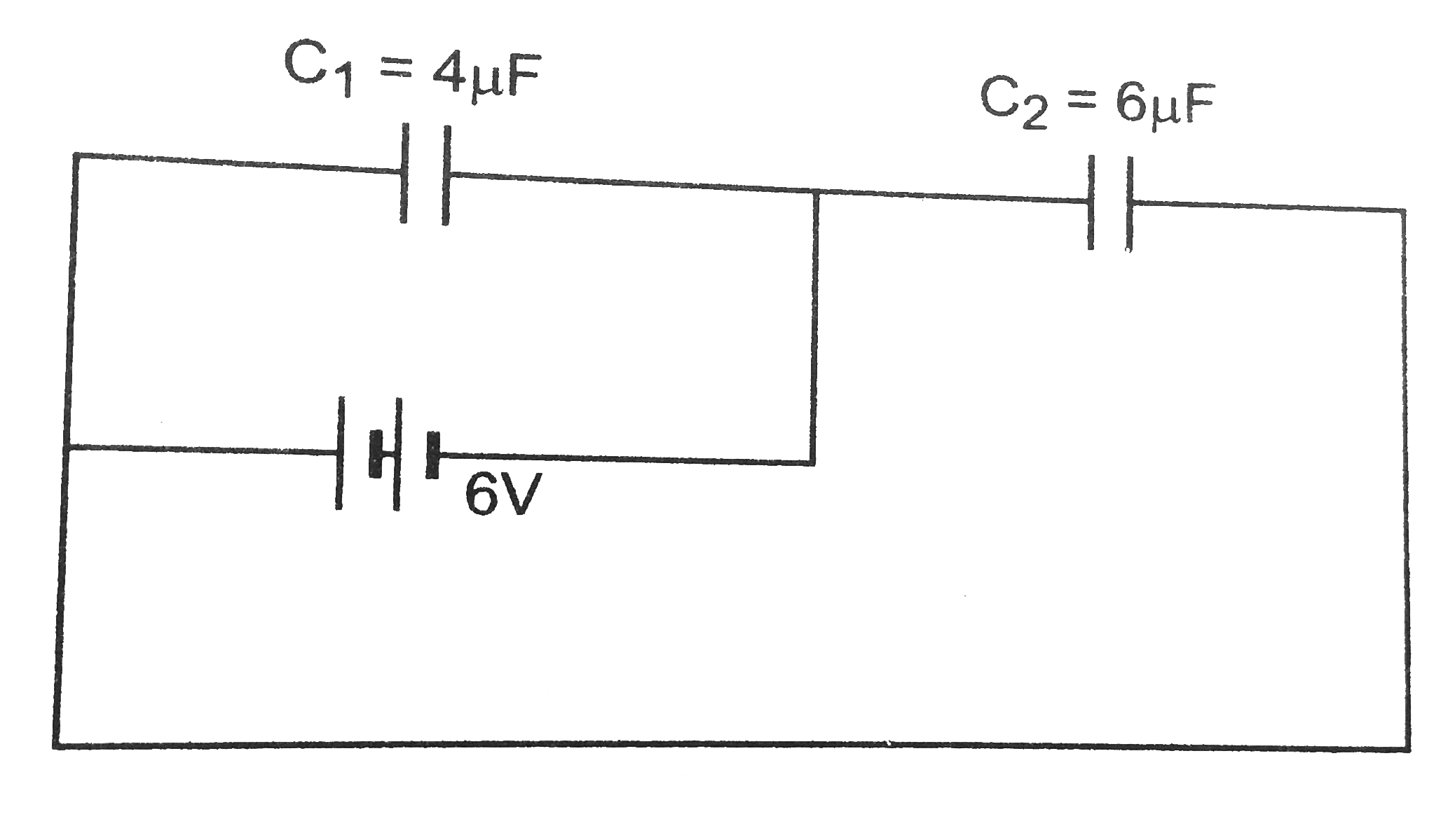
View SolutionTwo capacitors C1 and C2 are connected to a battery of 6V as shown in Fig. Find the charge on each capacitor.
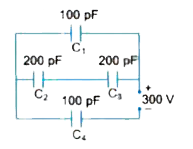
View SolutionObtain the equivalent capacitance of the network in Fig. For a 300 V supply, determine the charge and voltage across each 100 pF capacitor.
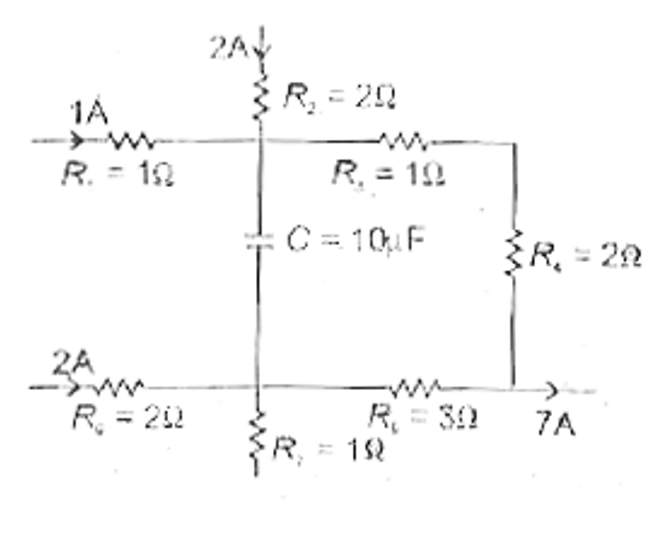
View SolutionGiven below is a part of network various values shown. Find the charge and energy stored in the capacitor .
View Solution