Find the expressions for time period and frequency
(i) in the oscillations of a liquid in a U tube
(ii) in the oscillations of a floating cylinder
To find the expressions for the time period and frequency of oscillations in a U-tube and a floating cylinder, we can follow these steps:
(i) Oscillations of a Liquid in a U-tube
1. Understanding the System:
- Consider a U-tube filled with a liquid to a height H. When the liquid is displaced by a small distance y, it creates a pressure difference that causes the liquid to oscillate.
2. Mass of the Liquid:
- The mass m of the liquid in the U-tube can be expressed as:
m=ρ⋅V=ρ⋅A⋅L
where ρ is the density of the liquid, A is the cross-sectional area of the tube, and L is the length of the liquid column.
3. Restoring Force:
- When the liquid is displaced by y, the restoring force Fr can be derived from the pressure difference:
Fr=−ΔP⋅A=−ρg(2y)A
where g is the acceleration due to gravity. The factor of 2y accounts for the displacement on both sides of the U-tube.
4. Equation of Motion:
- The restoring force can be equated to Hooke's law:
Fr=−ky
where k=2ρgA.
5. Time Period:
- The time period T of the oscillation can be calculated using:
T=2π√mk=2π√ρAL2ρgA=2π√L2g
- Since the total height of the liquid column is 2H, we can substitute L with 2H:
T=2π√Hg
6. Frequency:
- The frequency f is the reciprocal of the time period:
f=1T=12π√gH
(ii) Oscillations of a Floating Cylinder
1. Understanding the System:
- Consider a floating cylinder with a height L submerged in a liquid. When displaced, it experiences a buoyant force and weight.
2. Mass of the Cylinder:
- The mass m of the cylinder is given by:
m=ρc⋅V=ρc⋅A⋅L
where ρc is the density of the cylinder.
3. Buoyant Force:
- The buoyant force Fb acting on the cylinder when it is displaced by a distance y is:
Fb=σ⋅Vdisplaced⋅g=σA(L+y)g
where σ is the density of the liquid.
4. Restoring Force:
- The restoring force Fr when displaced is:
Fr=Fb−mg=σA(L+y)g−ρcAg
- Simplifying gives:
Fr=−σAgy
5. Equation of Motion:
- This can be expressed in the form of Hooke's law:
Fr=−ky
where k=σAg.
6. Time Period:
- The time period T of oscillation is given by:
T=2π√mk=2π√ρcALσAg=2π√ρcLσg
7. Frequency:
- The frequency f is:
f=1T=12π√σgρcL
Summary of Results
- For the U-tube:
- Time Period: T=2π√Hg
- Frequency: f=12π√gH
- For the Floating Cylinder:
- Time Period: T=2π√ρcLσg
- Frequency: f=12π√σgρcL
- Consider a U-tube filled with a liquid to a height H. When the liquid is displaced by a small distance y, it creates a pressure difference that causes the liquid to oscillate.
- The mass m of the liquid in the U-tube can be expressed as:
m=ρ⋅V=ρ⋅A⋅L
where ρ is the density of the liquid, A is the cross-sectional area of the tube, and L is the length of the liquid column.
- When the liquid is displaced by y, the restoring force Fr can be derived from the pressure difference:
Fr=−ΔP⋅A=−ρg(2y)A
where g is the acceleration due to gravity. The factor of 2y accounts for the displacement on both sides of the U-tube.
- The restoring force can be equated to Hooke's law:
Fr=−ky
where k=2ρgA.
- The time period T of the oscillation can be calculated using:
T=2π√mk=2π√ρAL2ρgA=2π√L2g
- Since the total height of the liquid column is 2H, we can substitute L with 2H:
T=2π√Hg
- The frequency f is the reciprocal of the time period:
f=1T=12π√gH
- Consider a floating cylinder with a height L submerged in a liquid. When displaced, it experiences a buoyant force and weight.
- The mass m of the cylinder is given by:
m=ρc⋅V=ρc⋅A⋅L
where ρc is the density of the cylinder.
- The buoyant force Fb acting on the cylinder when it is displaced by a distance y is:
Fb=σ⋅Vdisplaced⋅g=σA(L+y)g
where σ is the density of the liquid.
- The restoring force Fr when displaced is:
Fr=Fb−mg=σA(L+y)g−ρcAg
- Simplifying gives:
Fr=−σAgy
- This can be expressed in the form of Hooke's law:
Fr=−ky
where k=σAg.
- The time period T of oscillation is given by:
T=2π√mk=2π√ρcALσAg=2π√ρcLσg
- The frequency f is:
f=1T=12π√σgρcL
- For the U-tube:
- Time Period: T=2π√Hg
- Frequency: f=12π√gH
- Time Period: T=2π√ρcLσg
- Frequency: f=12π√σgρcL
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Advanced Problems For Competitions20videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - NCERT EXERCISES WITH SOLUTIONS19videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Short Answer Questions104videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
Similar Questions
Knowledge Check
- Question 1 - Select One
Motion of an oscillating liquid column in a U-tube is
Aperiodic but not simple harmonicBnon-periodicCsimple harmonic and time period is independent of the density of the liquidDsimple harmoni and time-period is directly proportional to the density of the liquid. - Question 2 - Select One
Motion of an oscillating liquid column in a U-tube is
Aperiodic but not simple harmonicBnon-periodicCsimple harmonic and time period is independent of the density of the liquidDsimple harmonic and time period is directly proprotional to the density of the liquid - Question 3 - Select One
Motion of an oscillating liquid column in a U -tube is :
Aperiodic but not simple harmonicBnon periodicCsimple harmonic and time period is independent of the density of the liquidDsimple harmonic and time period depends on the density of the liquid
Oscillation Of A Floating Body In A Liquid
View SolutionDerive an expression for the time -period of the horizontal oscillation of a massless loaded spring.
View SolutionIn the diagram shown find the time period of pendulum for small oscillations
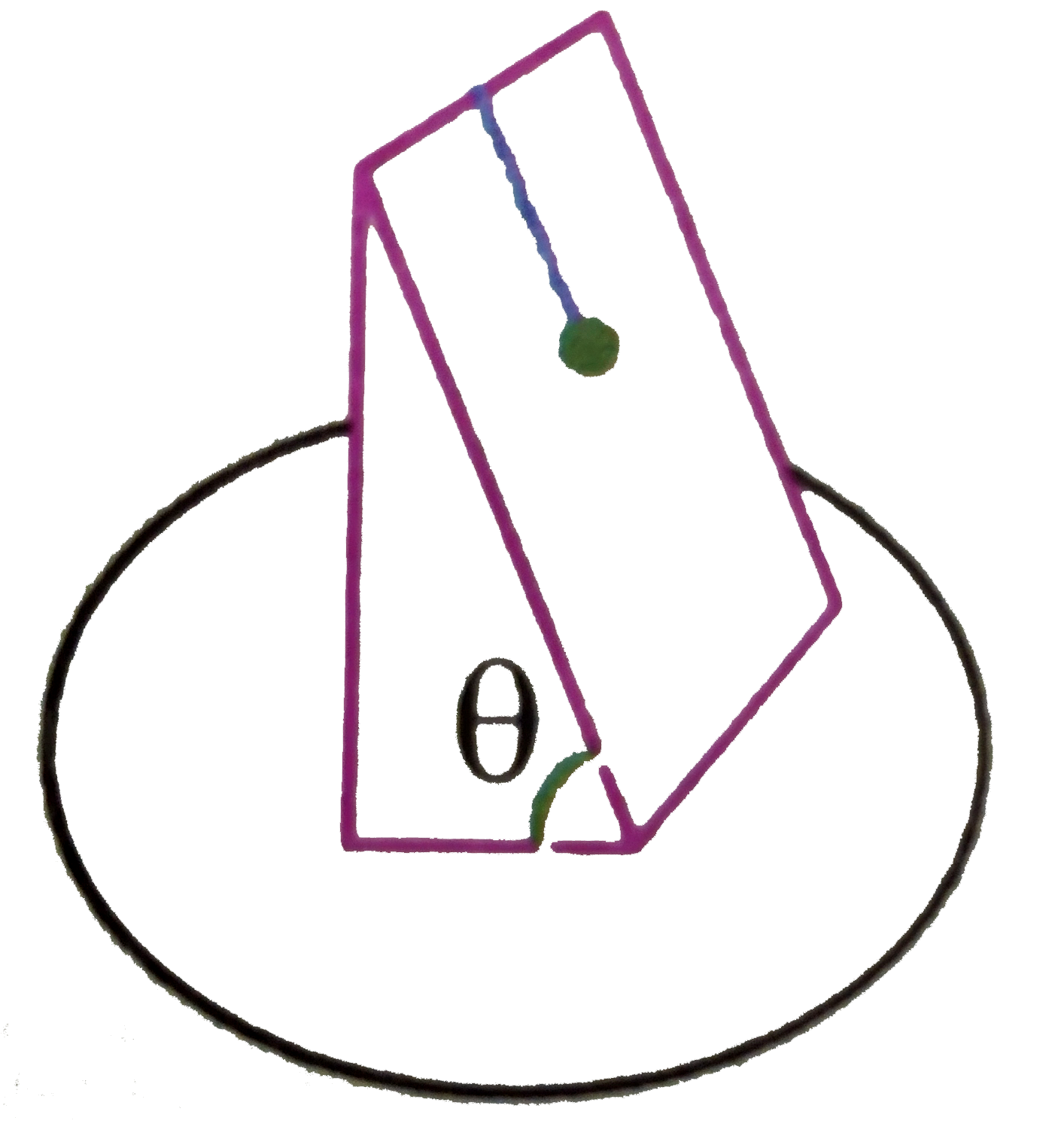 View Solution
View SolutionMotion of an oscillating liquid column in a U-tube is
View SolutionTime period of oscillation of a magnetic needle is
View Solution

