Find the magnetic field at the ccentre of a current carrying conductor bent in the form of an arc subtending angle θ at its centre. Radius of the arc is R
Strategy: Let the arc lie in x-y plane with its centre at the origin. Consider a small current element i→dl as shown. The field due to this element at the centre can be obtained by Biot-Savart law
To find the magnetic field at the center of a current-carrying conductor bent in the form of an arc subtending an angle θ at its center with a radius R, we can follow these steps:
1. Understanding the Setup:
- We have a current-carrying arc of radius R that subtends an angle θ at the center. The arc lies in the x-y plane with its center at the origin.
2. Applying the Biot-Savart Law:
- According to the Biot-Savart law, the magnetic field dB due to a small current element idl at a distance R from the center is given by:
dB=μ04πidlsinϕR2
- Here, ϕ is the angle between the current element dl and the line connecting the element to the point where the field is being calculated (the center of the arc).
3. Determining dl:
- For an arc, the length of the current element dl can be expressed in terms of the angle dϕ:
dl=Rdϕ
4. Substituting into the Biot-Savart Law:
- Since the angle ϕ is 90∘ (as dl is perpendicular to the radius at the center), we have sinϕ=1:
dB=μ04πiRdϕR2=μ0i4πRdϕ
5. Integrating to Find Total Magnetic Field:
- To find the total magnetic field B at the center, we integrate dB from 0 to θ:
B=∫θ0dB=∫θ0μ0i4πRdϕ
- This simplifies to:
B=μ0i4πR∫θ0dϕ=μ0i4πR(ϕ)θ0=μ0i4πRθ
6. Final Result:
- Therefore, the magnetic field at the center of the arc is:
B=μ0iθ4πR
- We have a current-carrying arc of radius R that subtends an angle θ at the center. The arc lies in the x-y plane with its center at the origin.
- According to the Biot-Savart law, the magnetic field dB due to a small current element idl at a distance R from the center is given by:
dB=μ04πidlsinϕR2
- Here, ϕ is the angle between the current element dl and the line connecting the element to the point where the field is being calculated (the center of the arc).
- For an arc, the length of the current element dl can be expressed in terms of the angle dϕ:
dl=Rdϕ
- Since the angle ϕ is 90∘ (as dl is perpendicular to the radius at the center), we have sinϕ=1:
dB=μ04πiRdϕR2=μ0i4πRdϕ
- To find the total magnetic field B at the center, we integrate dB from 0 to θ:
B=∫θ0dB=∫θ0μ0i4πRdϕ
- This simplifies to:
B=μ0i4πR∫θ0dϕ=μ0i4πR(ϕ)θ0=μ0i4πRθ
- Therefore, the magnetic field at the center of the arc is:
B=μ0iθ4πR
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration
14 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself
27 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
The magnetic field at the centre of the current carrying coil is
View SolutionFind magnetic field at O due to the current carrying conductor as shown in the figure.
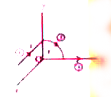
View SolutionFind the magnetic field at centre P due to current i in the conductor as shown in fig.

View SolutionThe magnetic field at centre O of the arc in Fig.
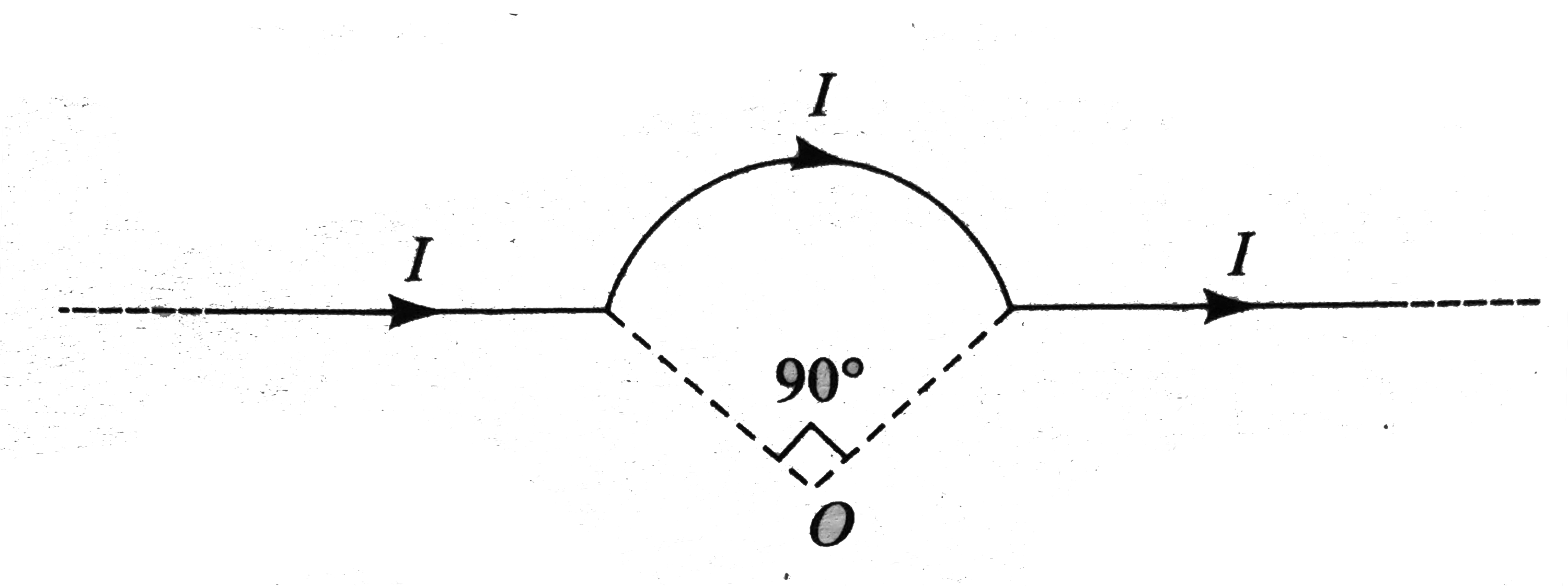
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionRatio of magnetic field at the centre of a current carrying coil of radius R and at a distance of 3R on its axis is
View SolutionThe magnetic field at centre of a hexagonal coil of side l carrying a current I is

View SolutionA piece of wire 20 cm long is bent into the form of an arc of a circle, subtending an angle of 60∘ at its centre. Find the radius of the circle.
View SolutionThe magnetic field at the origin due to a current element I (→dl)placedataposi→n(→r)is
View SolutionThe ratio of the magnetic field at the centre of a current carrying circular coil to its magnetic moment is x. If the current and radius both are doubled the new ratio will become
View Solution
