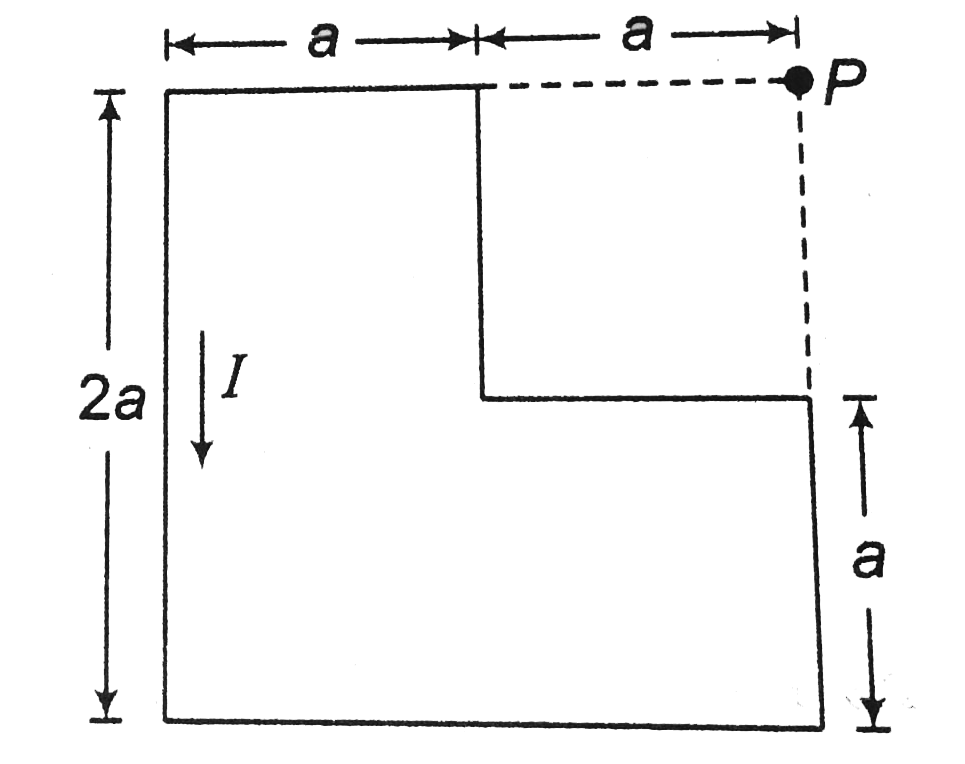
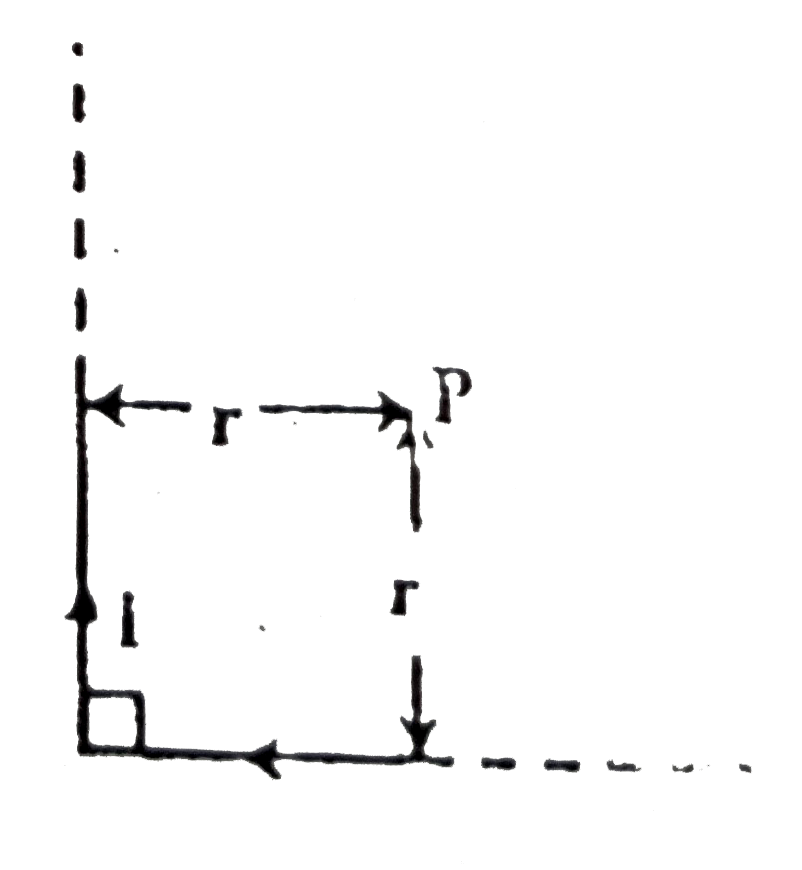
Find the magnetic field at the point P in figure. The curved portion is a semicircle and the straight wires are long.

Solution: The magnetic field at P due to any current
element in the figure is perpendicular to the plane of
the figure and coming out of it. The field due to the
upper straight wire is
B_1 = 1/2 xx ((mu_0)i/2pi (d/2)) = ((mu_0)i/(2 pi d))
Same is the field B2 due to the lower straight wire. The
field due to the semicircle of radius (d//2) is
(B3)=12×((μ0)i2(d2))=((μ0)i2d)
The≠tfieldisB=(B1)+(B2)+(B3)=((μ0)i2d)[1+(2π)].
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Short Answer12videos
MAGNETIC FIELD DUE TO CURRENT
- BOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 112videos
MAGNETIC FIELD DUE TO CURRENT
- BOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Exercises61videos
MAGNETIC FIELD DUE TO CURRENT
- BOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises61videos
MAGNETIC FIELD
- BOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises9videos
MAGNETIC PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
What will be the magnetic field at point P in the figure below?
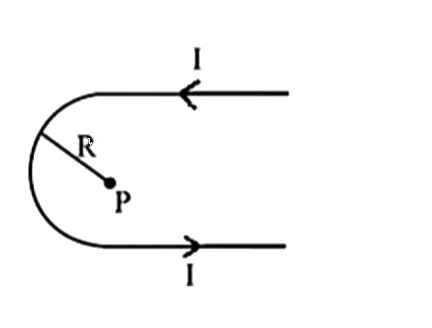 Aμ0i4R34Bμ0i4R(2π+1)Cμ0i2R(2π+1)D2μ0i2R(2π+1)
Aμ0i4R34Bμ0i4R(2π+1)Cμ0i2R(2π+1)D2μ0i2R(2π+1) - Question 2 - Select One
The magnetic field at the centre of semicircle o in the figure is
 AB=μ0i4rBμ0i4r(1+2π)Cμ0i4πr(π−2)Dμ0i4πr(π+2)
AB=μ0i4rBμ0i4r(1+2π)Cμ0i4πr(π−2)Dμ0i4πr(π+2) - Question 3 - Select One
The magnetic field at the centre of semicircle o in the figure is
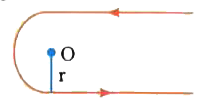 AB=μ0i4rBμ0i4r(1+2π)Cμ0i4πr(π−2)Dμ0i4πr(π+2)
AB=μ0i4rBμ0i4r(1+2π)Cμ0i4πr(π−2)Dμ0i4πr(π+2)
(a) Find the magnetic field at the point O if the wire carrying a current i has the shape shown. The radius of the current part of the wire is R, the linear parts of the wire are very long.
(i)
(ii)
(iii)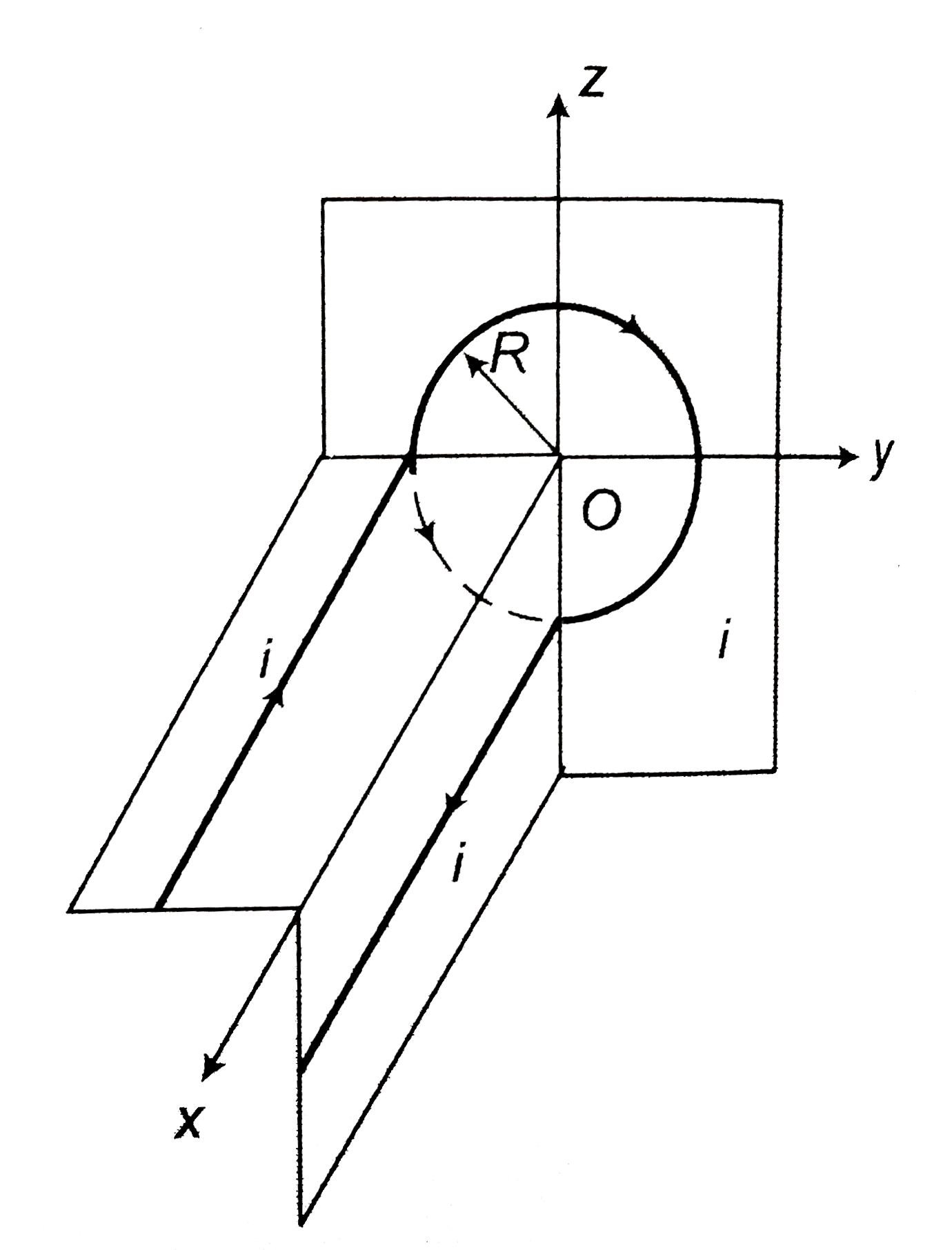
(b) A long straight wire along the z-axis carriers a current i in negative z-direction. Find magnetic field in vector from at a point having co-ordinates (x,y) on z=0 plane.
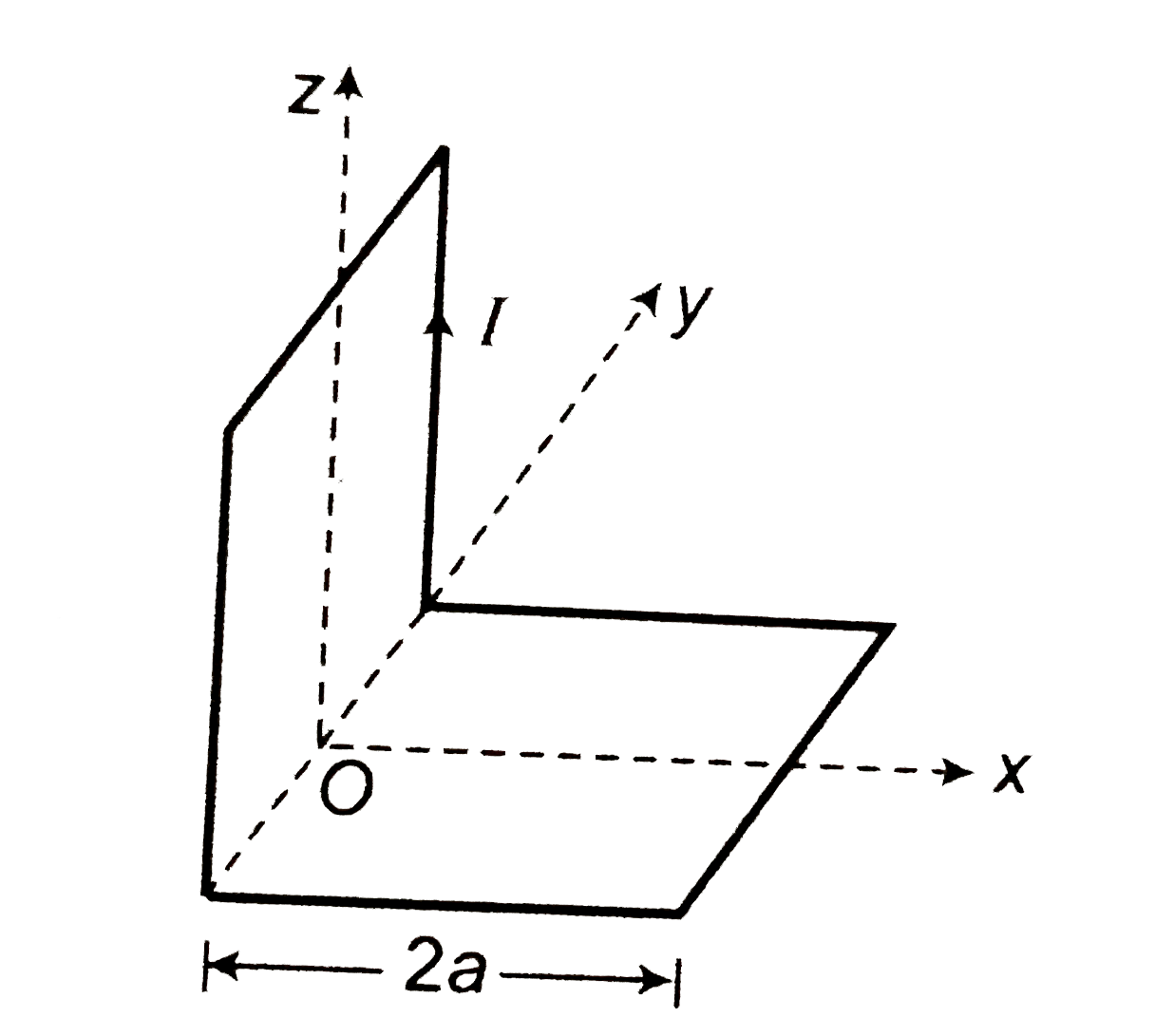
(c) A non-coplaner loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop of length 2a. find unit vector along magnetic field magnetic filed at the point P(a,0,a).
 View Solution
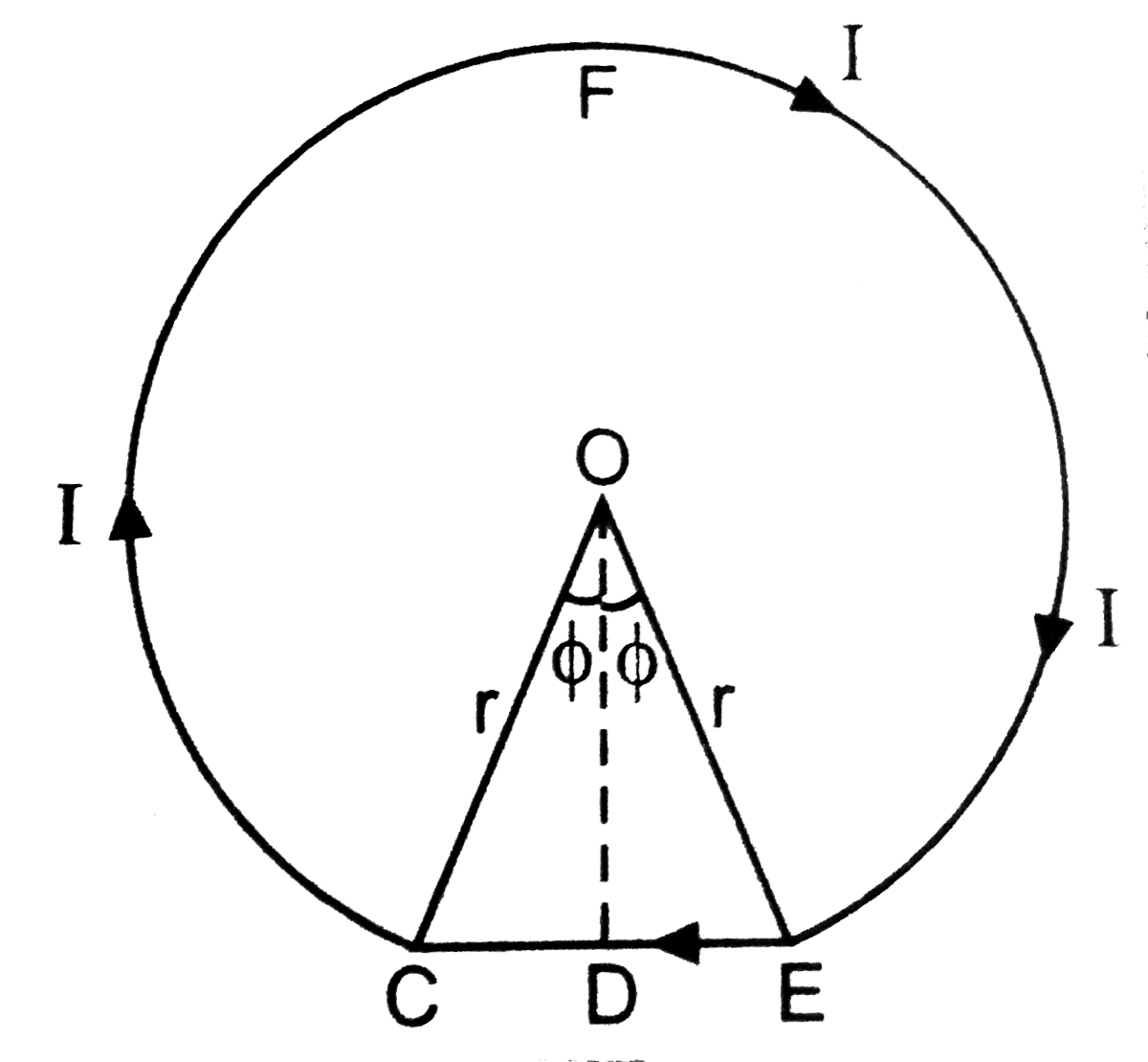
View SolutionFind the total magnetic induction at point O due to current through curved portion and straight portion in the figure.
 View Solution
View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure below
 View Solution
View SolutionCalculate the magnetic field at a point P. 0.5m away from an infinitely long straight wire carrying current of 90 A.
View SolutionThe magnetic field strength at a point P distant r due to an infinite straight wire carrying a current i is as shown in the figure
 View Solution
View Solution