Find the maximum frequency, the X-ray emitted by an X-ray tube operating at 30kV
To find the maximum frequency of the X-ray emitted by an X-ray tube operating at 30 kV, we can follow these steps:
Step 1: Understand the relationship between energy and frequency
The energy of a photon is given by the equation:
E=hν
where:
- E is the energy of the photon,
- h is Planck's constant (6.626×10−34Js),
- ν is the frequency of the photon.
Step 2: Relate the energy to the voltage
In an X-ray tube, the energy gained by the electrons when accelerated through a potential difference V is given by:
E=eV
where:
- e is the elementary charge (1.602×10−19C),
- V is the voltage (in this case, 30kV=30×103V).
Step 3: Set the two energy equations equal
To find the maximum frequency, we set the two expressions for energy equal to each other:
eV=hν
Step 4: Solve for frequency
Rearranging the equation gives:
ν=eVh
Step 5: Substitute the values
Now, substituting the known values:
- e=1.602×10−19C
- V=30×103V
- h=6.626×10−34Js
We first calculate eV:
eV=(1.602×10−19C)(30×103V)=4.806×10−15J
Now, we convert this energy into electron volts (since 1eV=1.602×10−19J):
eV=30keV=30,000eV
Now we can calculate the frequency:
ν=30,000eV4.14×10−15eV s
Step 6: Calculate the frequency
Calculating this gives:
ν=30,0004.14×10−15≈7.24×1018Hz
Final Answer
The maximum frequency of the X-ray emitted by the X-ray tube operating at 30 kV is approximately:
ν≈7.24×1018Hz
The energy of a photon is given by the equation:
E=hν
where:
- E is the energy of the photon,
- h is Planck's constant (6.626×10−34Js),
- ν is the frequency of the photon.
In an X-ray tube, the energy gained by the electrons when accelerated through a potential difference V is given by:
E=eV
where:
- e is the elementary charge (1.602×10−19C),
- V is the voltage (in this case, 30kV=30×103V).
To find the maximum frequency, we set the two expressions for energy equal to each other:
eV=hν
Rearranging the equation gives:
ν=eVh
Now, substituting the known values:
- e=1.602×10−19C
- V=30×103V
- h=6.626×10−34Js
eV=(1.602×10−19C)(30×103V)=4.806×10−15J
eV=30keV=30,000eV
ν=30,000eV4.14×10−15eV s
Calculating this gives:
ν=30,0004.14×10−15≈7.24×1018Hz
The maximum frequency of the X-ray emitted by the X-ray tube operating at 30 kV is approximately:
ν≈7.24×1018Hz
Topper's Solved these Questions
- X-RaysBOOK - HC VERMA ENGLISHCHAPTER - X-RaysEXERCISE - Objective 1
13 Videos
- X-RaysBOOK - HC VERMA ENGLISHCHAPTER - X-RaysEXERCISE - Objective 2
8 Videos
- THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTBOOK - HC VERMA ENGLISHCHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Short Question
9 Videos
Similar Questions
Find maximum frequency of X-rays produced by an X-ray tube operating at a tube potential of 66 kV.
View SolutionFind the minimum wavelngth of X - ray emitted by X - ray tube , which is operating at 15kV accelerating voltage.
View SolutionThe X-rays beam coming from an X-ray tube will be
View SolutionFigure below shows a simple diagram of a modern X ray tube. (i.e. Coolidge tube).
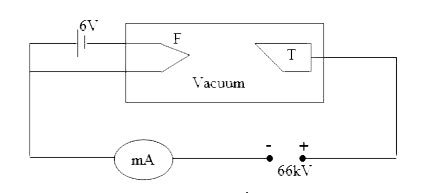
(i) Find the minimum wavelength of the X rays emitted by the X ray tube.
(ii) What will be the effect of replacing the 6V battery with a 9V battery on the emitted X rays?
View Solutionfind the minimum wavelength of the emitted X rays, when an X-ray tube is operated at 50 kV.
View SolutionFind the cutoff wavelength for the continuous X-rays coming form an X-ray tube operating at 30 kV.
View SolutionUsing the constants given below:
speed of light in vacuum (c) 3.0×108ms−1 Planck.s constant (h) =6.6×10−4Js Charge of a proton (e) =1.6×10−1^∘C, find the minimum wavelength of the emitted X rays, when an X ray tube is operated at 50 kV.
View SolutionFind the cut off wavelength for the continuous X - rays coming from an X-ray tube operating at 40 kV.
View SolutionCalculate the maximum frequency and wavelength of X-ray produced in a tube maintained at 13.26 kV.
View SolutionFind the cut off walelength for the continuous X - rays coming
form an X-ray tube operating at 40 kv.
View Solution
