Find the minimum speed at A so that the ball can reach at point B as shown in figure. Also discuss the motion of particle when T=0, v=0 simultaneously at θ=90∘
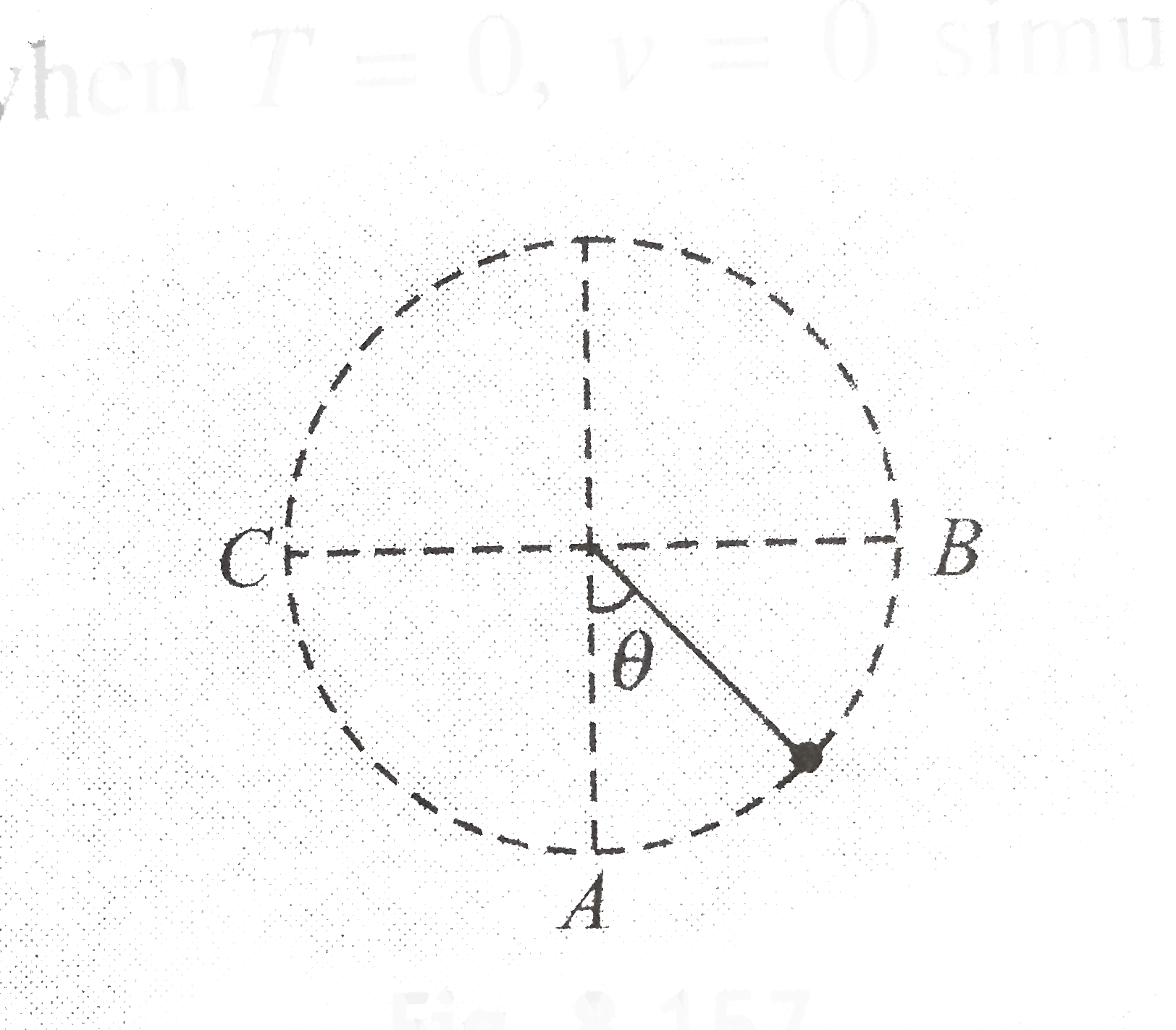
From energy conservation,
12mv2A+0=0+mgl
(for minimum speed, vB=0)
vmin=√2gl
At position B, v=0 and T=0.
Putting vB=0 or θ=90∘, in (i) ball will return back, motion is oscillatory
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
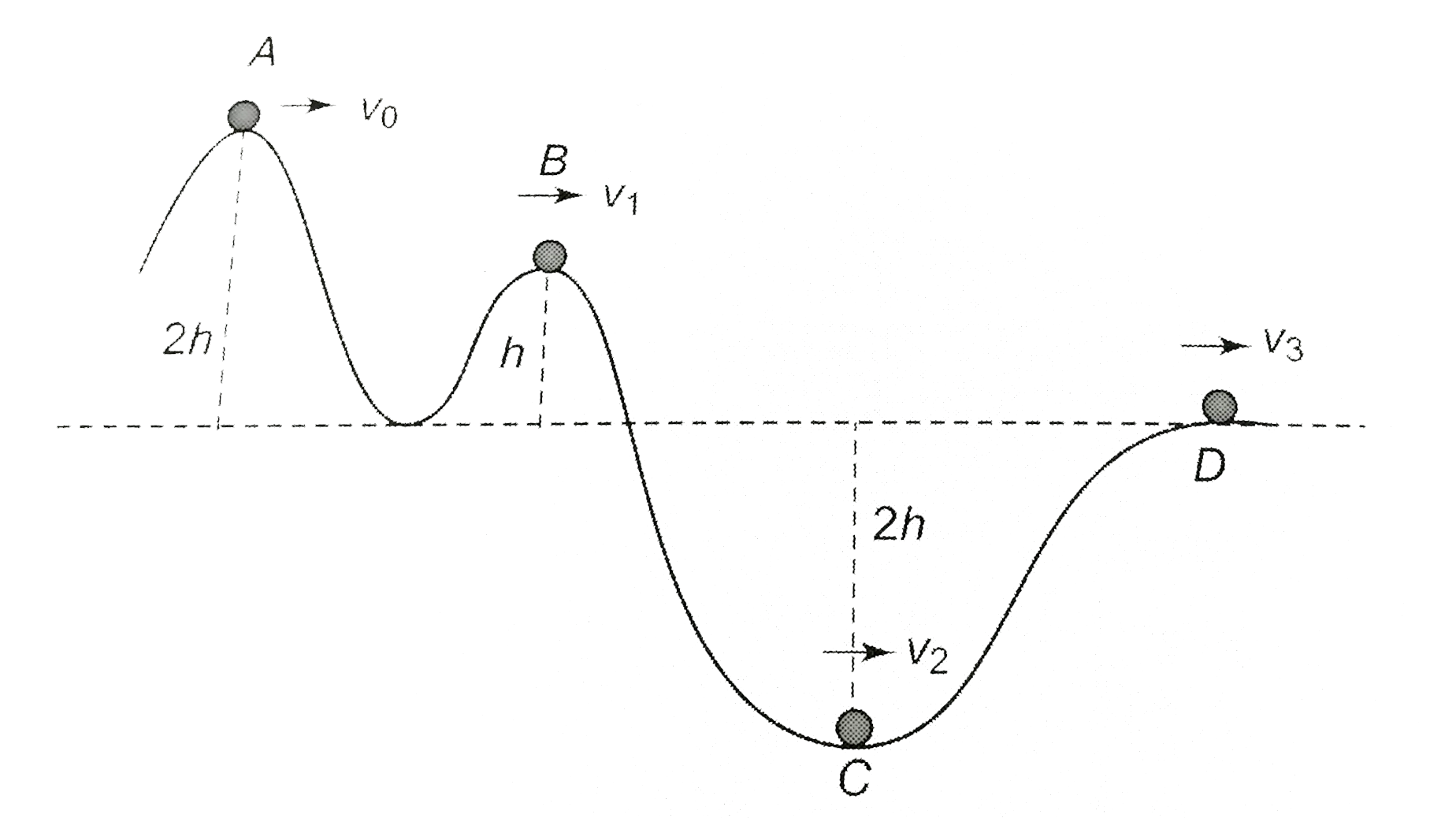
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and D
View SolutionThe magnitude of force acting on a particle moving along x-axis varies with time (t) as shown in figure. If at t = 0 the velocity of particle is v0, then its velocity at t=T0 will be

View Solution
Knowledge Check
The speed-time graph of a particle moving along a fixed direction as shown in the figure. The distance travelled by the particle between t = 0 s to t = 10 s is
 A20 mB40 mC60 mD80 m
A20 mB40 mC60 mD80 mA projectile is projected with a velocityv0 at an angle θ with the horizontal as shown in figure. The angular momentum of particle about the origin:
 Ais zero when particle is at the originBis −mv3sin2θcosθ2gˆk when particle is at the highest point of trajectoryCis −2mv2sin2θcosθgˆk when particle is just about to hit groundDdownward force of gravity exerts a torque in −z direction.
Ais zero when particle is at the originBis −mv3sin2θcosθ2gˆk when particle is at the highest point of trajectoryCis −2mv2sin2θcosθgˆk when particle is just about to hit groundDdownward force of gravity exerts a torque in −z direction.A graph of acceleration versus time of a particle starting from rest at t=0 is as shown in figure. The speed of the particle at t=14s is
 A2ms−1B34ms−1C20ms−1D42ms−1
A2ms−1B34ms−1C20ms−1D42ms−1
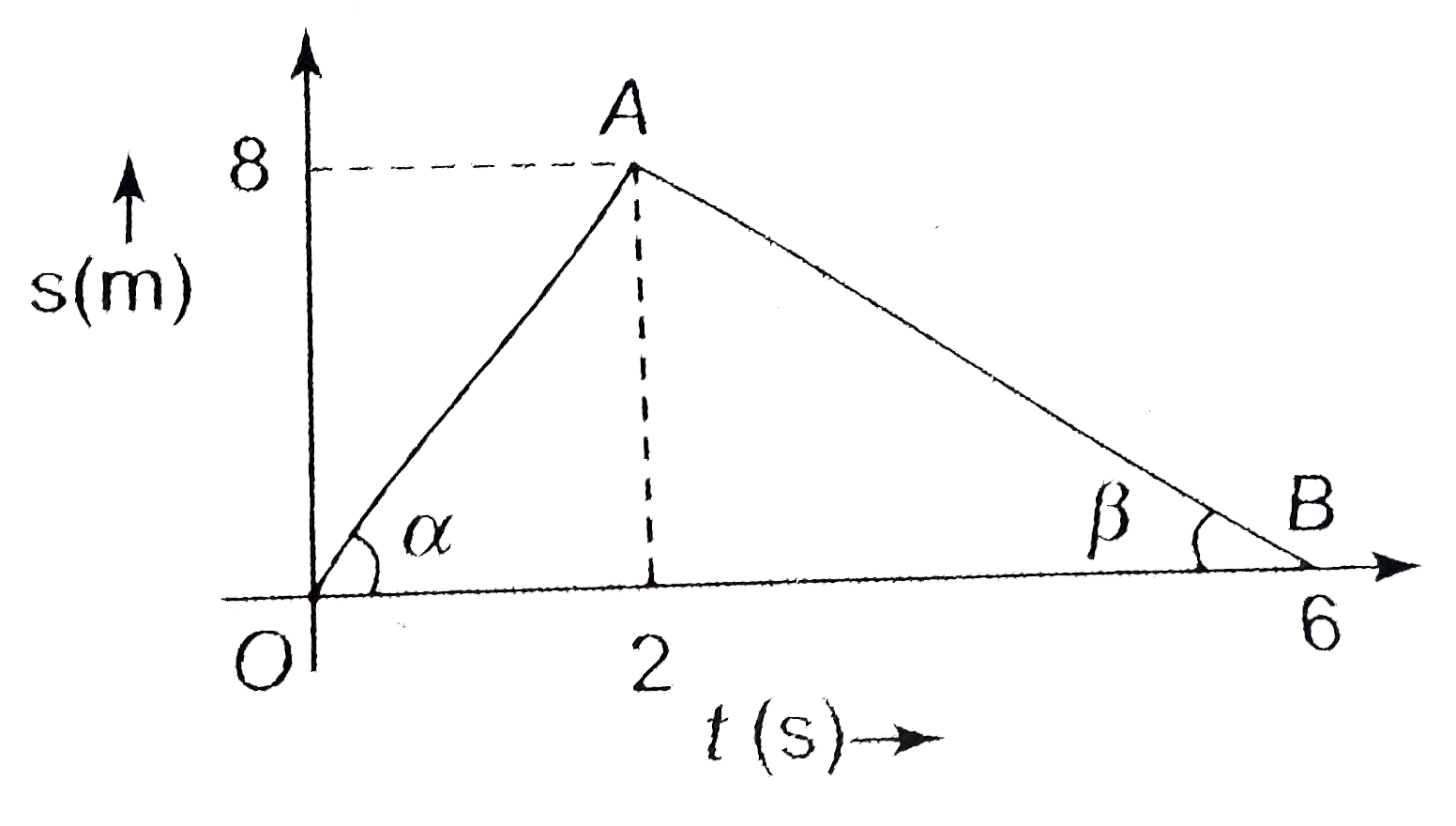
For a particle moving in a straight line, the position-time graph is as shown in the figure. Find the velocity of the particle at time t=1s and t=4s. Also sketch the v-t graph.
View SolutionA particle of mass m is projected with a speed v at an angle θ with the horizontal. Find the angular momentum of the particle about an axis passing through point of projection and perpendicular to the plane of motion of the particle.
(a) When the particle is at maximum height and
(b) When the particle is just about to collide with the horizontal surface
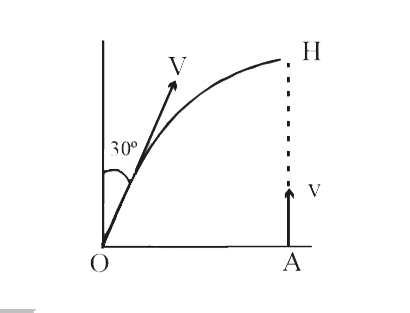
View SolutionA particle is projected with a speed V from a point O making an angle of 30∘ with the vertical. At the same instant, a second particle is thrown vertically upwards with a speed v from a point A. The two particle reach H, the highest point own the parabolic path of particle one simultaneously. Then ratio V/v is-
View SolutionA particle moves with a speed v in a circle of radius R .when the particle reaches from A to B as shown in the figure, then Y component of average velocity is
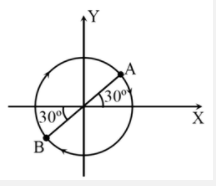
View SolutionPosition-time graph for a particle moving along x− direction is as shown in the figure. Average speed of the particle from t=0 to t=4 is :

View Solution