Find the moment of incrtia about the metric center of the given structure made up of one thin rod connecting two similar solid spheres as shown in Figure.
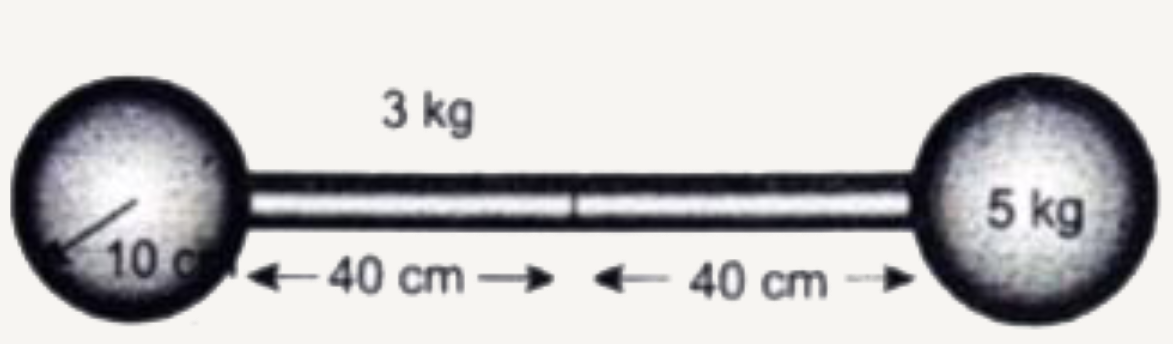
The structure is made up of three objects, one thin rod and two solid spheres. The mass of the rod, M= 3 kg and the total length of the rod, 1 - 80 cm -0.8 m The moment of inertia of the rod about its center of mass is,
Irod=112Ml2
Irod=112×3×(0.8)2=14×0.64
Irod=0.16kgm2
The mass of the sphere, M = 5 kg and the radius of the sphere, R=10 cm -0.1 m.
The moment of inertia of the sphere about its center of mass is, IC=25MR2.
The moment of inertia of the sphere about geometric center of the structure is Isph=IC+Md2
Where d=40cm+10cm+50cm=0.5m
Isph=25MR2+Md2
Isph=25×5×(0.1)2+5×(0.5)2
Isph=(0.×0.1)+(5×0.25)=0.02+1.25
Isph=1.27kgm2
As there are one rod and two similar solid spheres we can write the total moment of inertia (i) of the given geometric structure as I=Irod+(2×Isph)
I=(0.16)+(2×1.27)=0.16+2.54
I=2.7kgm2
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODIESBOOK - FULL MARKSCHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODIESEXERCISE - TEXTUAL QUESTIONS SOLVED ( MULTIPLE CHOICE QUESTIONS:)
15 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODIESBOOK - FULL MARKSCHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODIESEXERCISE - TEXTUAL QUESTIONS SOLVED ( SHORT ANSWER QUESTIOS)
17 Videos
- LAW OF MOTION BOOK - FULL MARKSCHAPTER - LAW OF MOTION EXERCISE - ADDITIONAL QUESTIONS SOLVED (SHORT ANSWER QUESTIONS (3 MARKS & NUMERICALS))
16 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENT BOOK - FULL MARKSCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENT EXERCISE - ADDITIONAL QUESTIONS SOLVED ( SHORT ANSWER QUESTIONS (2 MARK))
20 Videos
Similar Questions
Knowledge Check

Find moment of inertia of a thin sheet of mass M in the shape of an equilateral triangle about an axis as shown in figure. The length of each side is LA3ML2/8B3√3ML2/8C7ML2/8Dnone of theseFigure represents the moment of inertia of the solid sphere about an axis parallel to the diameter of the solid sphere and at a distance x from t. Which one of the following represents the variations of I with x ?
A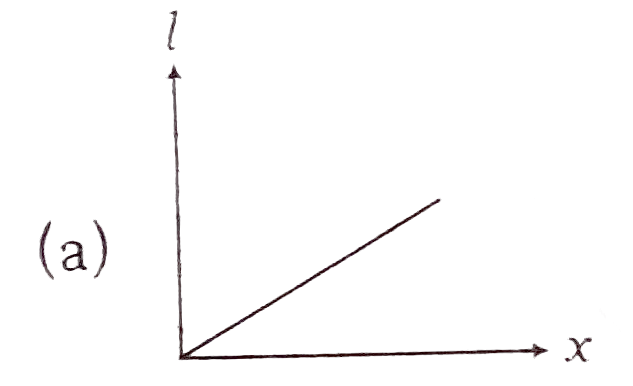 B
B C
C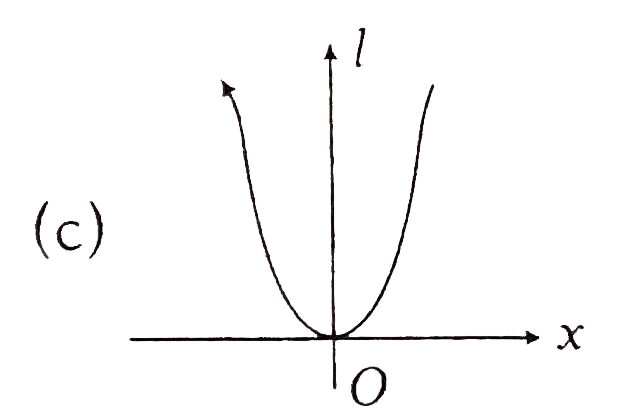 D
D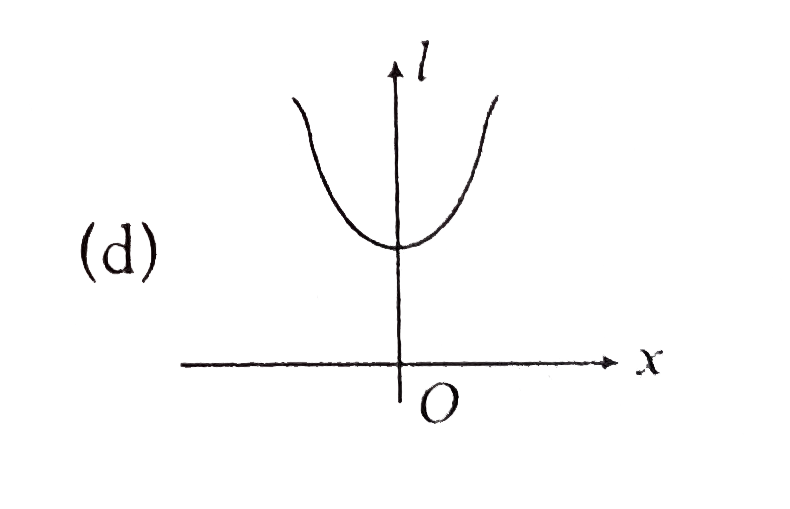
Find the moment of inertia of solid sphere of mass M about a diameter as shown in Fig.
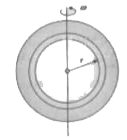
View SolutionA spherical cavity is formed a solid sphere by removing mass from it. The resultant configuration is shown in figure. Find out the moment of inertia this configuration about the axis through centre of the solid sphere as shown . Take mass M( uniform ) for the configuration and radius R for solid sphere and radius R/2 for cavity.
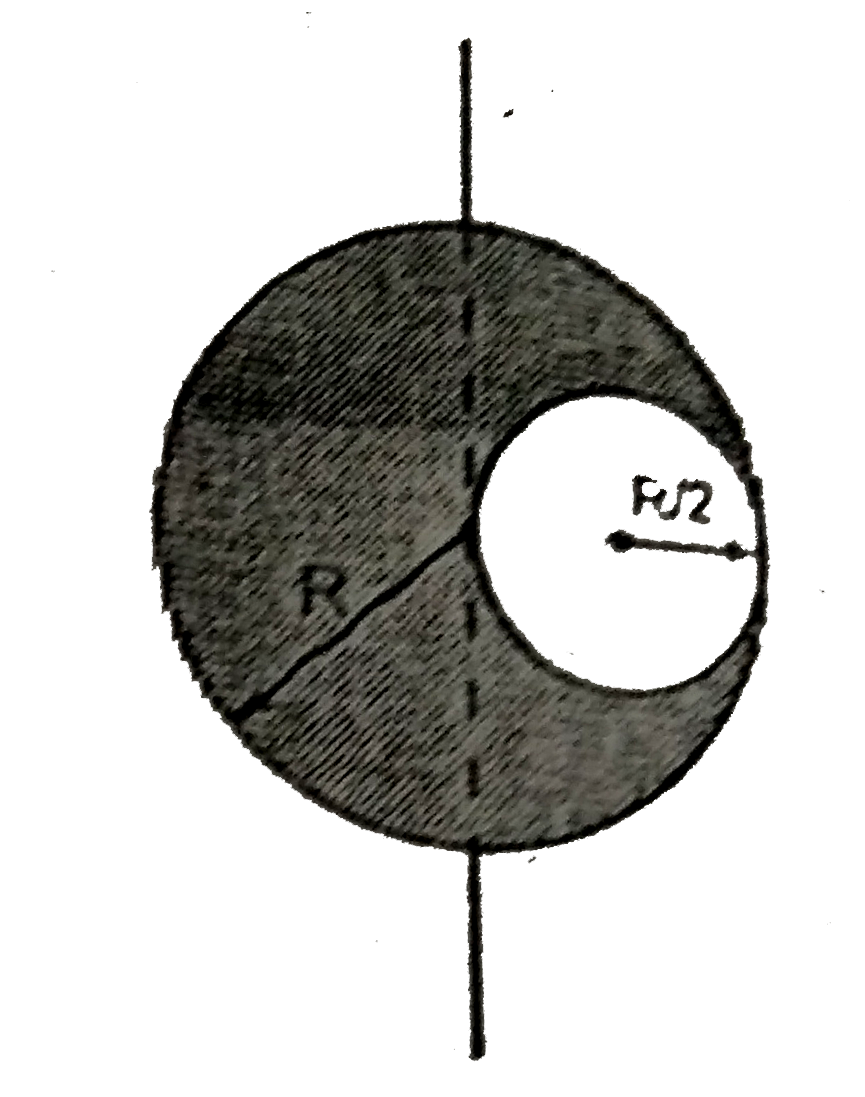
View Solution
Find moment of inertia of a thin sheet of mass M in the shape of an equilateral triangle about an axis as shown in figure. The length of each side is L
View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.

View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.

View SolutionFigure represents the moment of inertia of the solid sphere about an axis parallel to the diameter of the solid sphere and at a distance x from t. Which one of the following represents the variations of I with x ?
View Solution

