
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
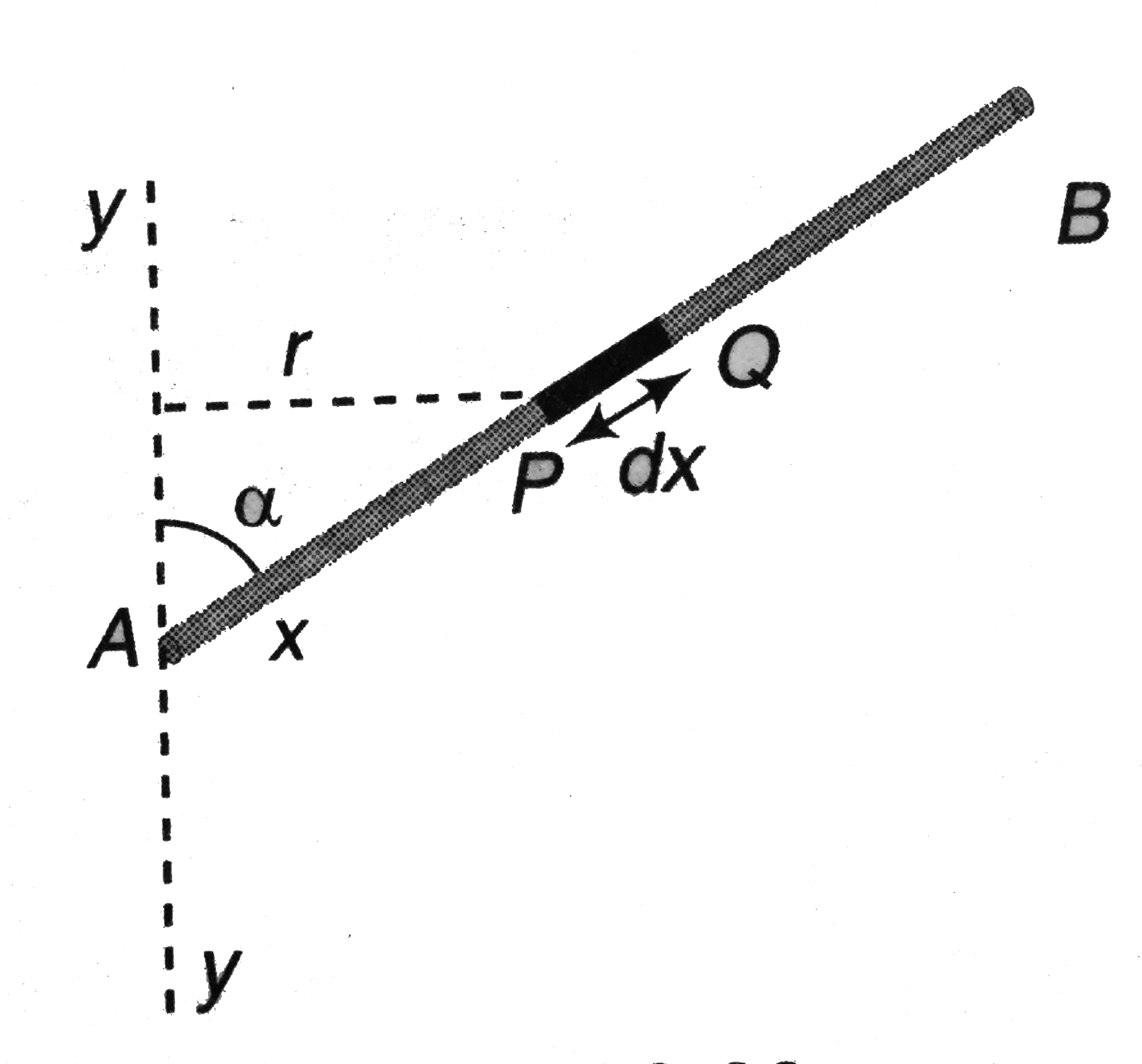
Mass per unit length of the rod =ml
Mass of an element PQ of the rod is dm=(ml)dx
jPerpendicular distance of this elemental mass about yy is r=xsinα
∴ moment of inertia of this small element of the rod (can be assumed as a point mass) about yy is
dI=(dm)r2=(mldx)(xsinα)2=(mlsin2α)x2dx
∴ moment of inertial of the complete rod,
I=∫x=lx=0dI=mlsin2α∫l0x2dx=ml23sin2α
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Examples
25 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Calculate the moment of inertia of the given rod about an axis CD
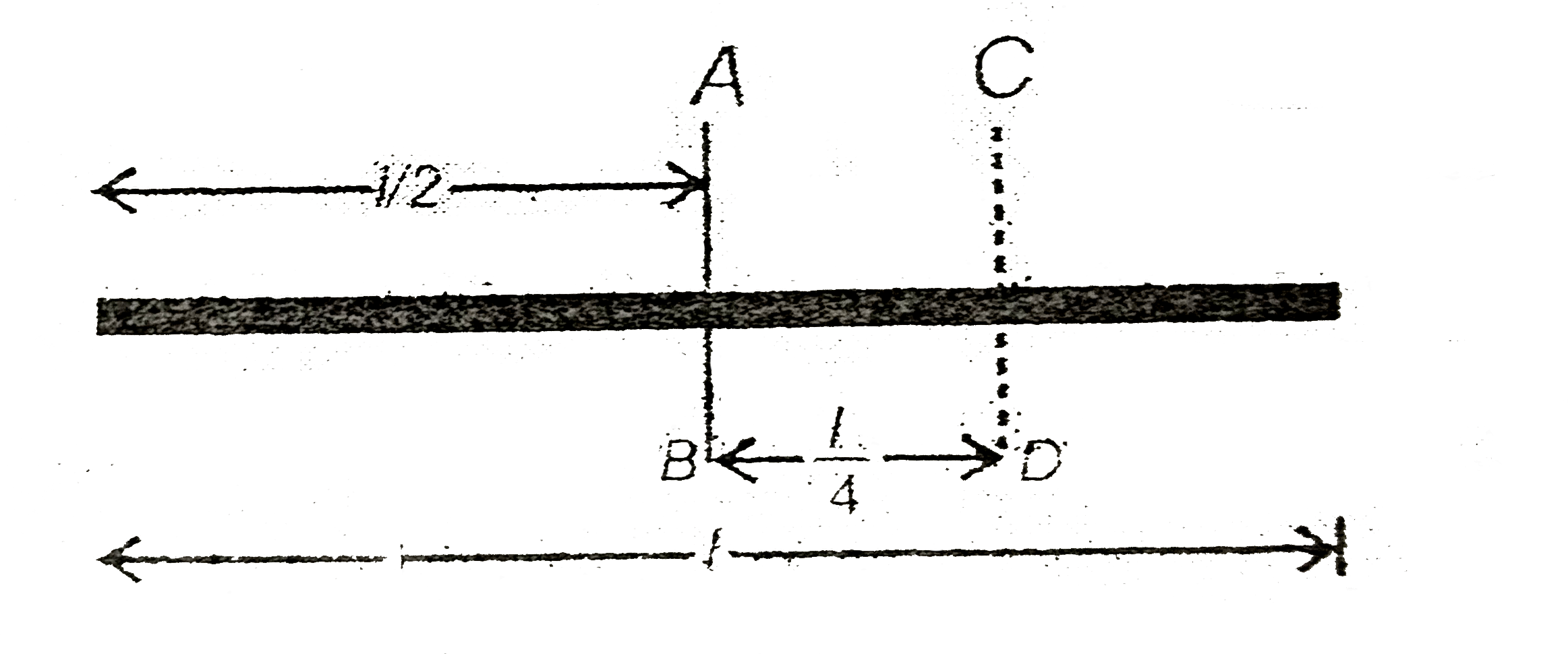
View SolutionCalculate the moment of inertia of the given rod about an axis CD.
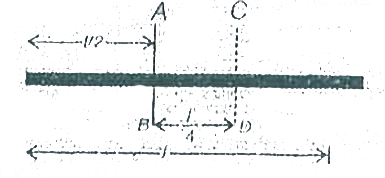
View SolutionLinear mss density (mass/length) of a rod depends on the distanec from one end (say A) as λx=(αx+β) here α and β are constants, find the moment of inertia of this rod about an axis passing through A and perpendicular to the rod. Length of the rod is l.
View SolutionA uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
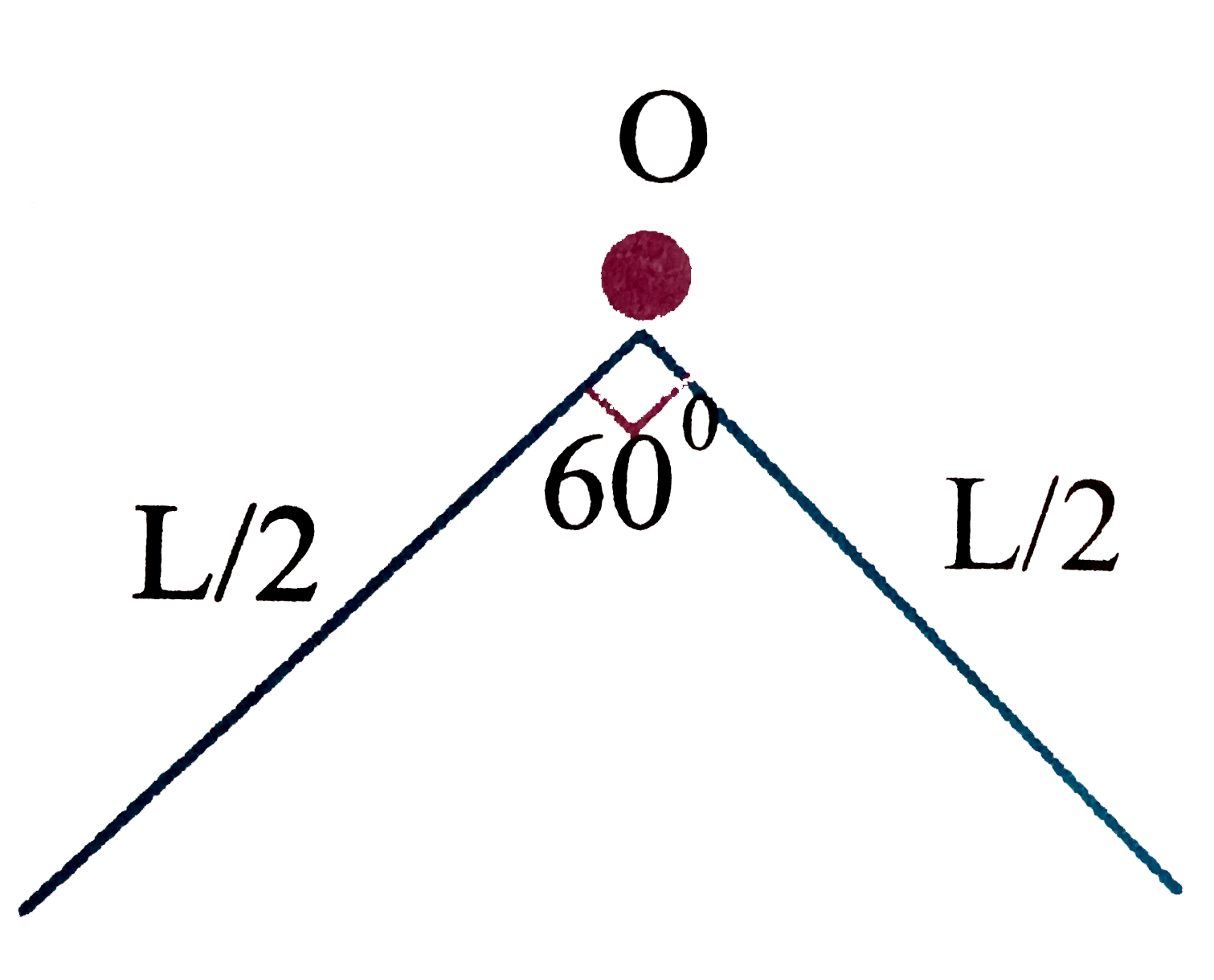
View SolutionA thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length R. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.
View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.

View SolutionA rod of length L is composed of a uniform length 1/2 L of wood mass is mw and a uniform length 1/2 L of brass whose mass is mb. The moment of inertia I of the rod about an axis perpendicular to the rod and through its centre is equal to
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.
View Solution
