Find the number of ratational levels per unit energy interval, dN/dE, for a diatomic molecule as a function of rotational energy E. Calculate of an magnitude for an iodine molecule in the state with rotational quantum number J=10. The distance between the nuclei of that molecule is equal to 267pm.
From the formula
J(J+1)ħ22I=E we get J(J+1)−2IE/ħ2
or (J+12)2−14=2IEħ2
Hence J=−12+√14+2IEħ2
writing J+1=−12+√14+2Iħ2(E+ΔE)
we find 1=√14+2Iħ2E+2Iħ2ΔE−√14+2IEħ2
√14+2Iħ2E⎡⎢
⎢⎣⎛⎜⎝1+ΔEE+ħ28I⎞⎟⎠1/2⎤⎥
⎥⎦
√14+2Iħ2E.ΔE2(E+ħ28I)
√2Iħ2ΔE2√(E+ħ28I)
The quantity dNdEis1ΔE. For large E it is
dNdE=√I2ħ2E
For an iodine molecule I=MId2/2=7.57×10−38gmcm2
Thus for J=10
dNdE=
⎷I2ħ2.ħ22IJ(J+1)=I√J(J+1)ħ2
Substitution gives
dNdE=1.04×104 levels per eV.
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Radioactivity
35 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Nuclear Reaction
42 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom
69 Videos
- DIRECT CURRENTBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions
15 Videos
Similar Questions
Find the angular momentum of an oxygen molecule whose rational energy is E=2.16meV and the distance between the nuclei is d=121pm.
View SolutionDetermine the angular rotation velocity of an S2 molecule promoted to the first exccited rotational level if the distance between its nuclei is d=189pm
View Solution
Knowledge Check
The key feature of Bohr'[s spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton we will extend this to a general rotational motion to find quntized rotantized rotational energy of a diatomic molecule assuming it to be right . The rate to energy applied is Bohr's quantization condition
it is found that the excitation from ground to the first excited state of rotation for the CO molecule is close to 4π×1011Hz then the moment of inertia of CO molecule about its center of mass is close to
(Takeh=2π×10−34Js)A2.76×10−46kgm2B1.87×10−46kgm2C4.67×10−47kgm2D1.17×10−47kgm2
For an HCI molecule find the rotational quantum numbers of two neighbouring levels whose energies differ by 7.86meV. The nuclei of the molecule are separated by distacne of 127.5pm.
View SolutionFor an HF molecule find the number of rotational levels located between the Zeroth and first excited vibrational levels assuming rorational states to be independent of vibrational ones. The natural vibration frequency of this molecule is equal to 7.79.1014rad/s and the distance between the nuclie is 91.7pm.
View SolutionShow that the frequency intervals between the neighbouring spectral lines of a true ratational spectrim of a diatomic molecules are equal. Find the moment of intertial and the distance between the nuclei of a CH molecule if the intervals between the neighbouring lines of the true rotational spectrum of these molecules are equal to Δω=5.47.1012s−1
View SolutionThe key feature of Bohr's spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid.The rule to be applied is Bohr's quantization condition.
it is found that the excitation from ground to the first excited state of rotation for the CO molecule is close to 4π×1011Hz then the moment of inertia of CO molecule about its center of mass is close to
(Takeh=2π×10−34Js)
View SolutionThe natural vibration frequency of a hydrogen molecule is equal to 8.25.1014S−1, the distance between the nuclei is 74pm, Find the ratio of the number of these molecules at the first excited vibrational level (v=1) to the number of molecules at the first excited rotational level (J=1) at a temperature T=875K. It should be remembered that degeneracy of rotational levels is equal to 2J+1.
View SolutionThe distance between the atomic centres in a nitrogen molecule is 1.094×10−10m. Find the moment of inertia of the molecule and the temperature at which molecular collisions cause the state of the rotational motion to change.
View SolutionRotational energy levels of diatomic molecules are well described by the formula EJ=BJ(J+1), where J is the rotational quantum number of the molecule and B its rotational constant. B is related to the reduced
mass μ and the bond length R of the molecule through the equation B=h28π2μR2.
In general, spectroscopic transitions appear at photon energies which are equal to the energy difference between appropriate states of a molecule (hv=ΔE). The observed rotational transitions occur between adjacent rotational levels, hence ΔE=EJ+1−EJ=2B(J+1). Consequently, successive rotational transitions that appear on the spectrum (such as the one shown here) follow the equation h(Δυ)=2B.
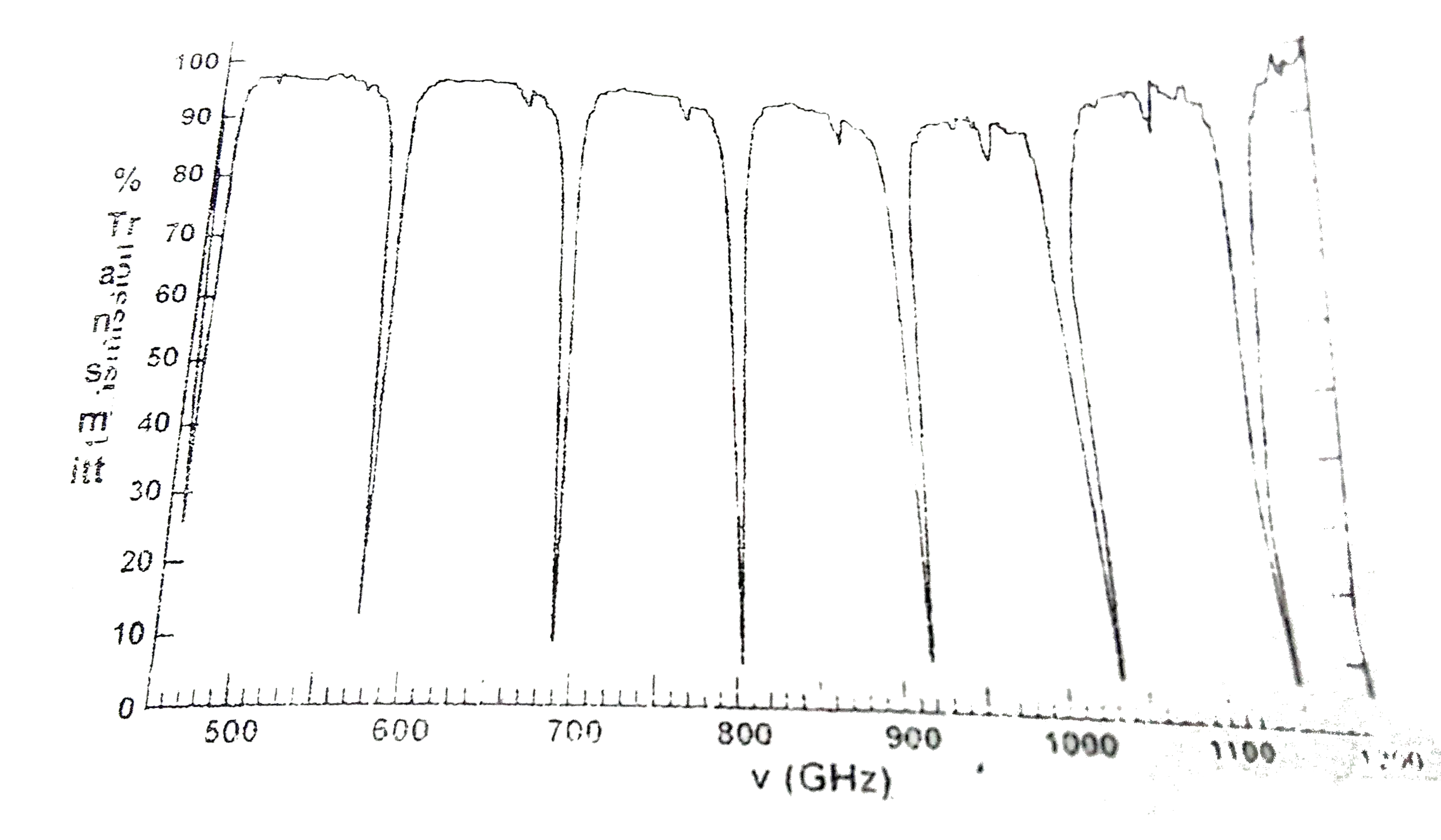
By inspecting the spectrum provided, determine the following quantities for ^(2)C^(p)Cwithap∝riateunits<br>(a)Deltaupsilon(b)B(c)R
View Solution
