Find the period of small vertical oscillations of a body with mass m in the system illustrated in figure. The stiffness values of the springs are x1 and x2, their masses are negligible.
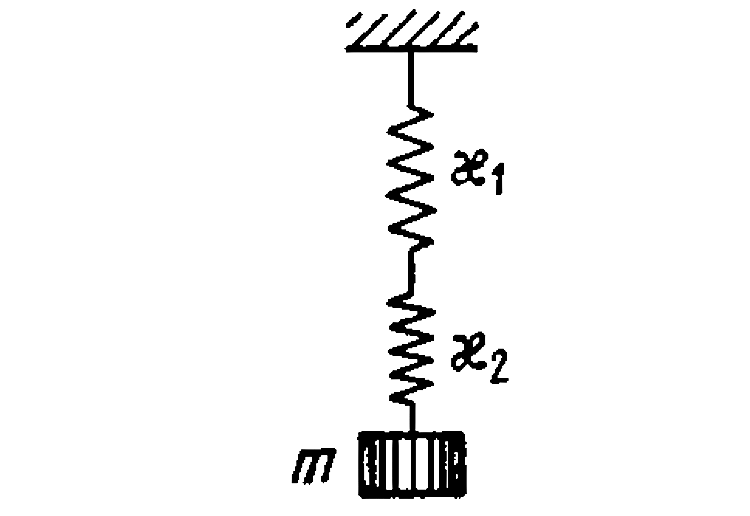
During the vertical oscillation let us locate the bock at a vertical down distance x from its equilibrium position . At his moment if x1 and x2 are the additional or further elongation of the upper & lower springs relative to the equilibrium position, then the net unbalanced force on the block will be k2x2 directed in upward direction. Hence
−k2x2=m..x............(1)
we also have x=x1+x2......(2)
As the springs are massless and initially the net force on the spring is also zero so for the spring
k1x1=k2x2.......(3)
Solving the Eqns (1),(2) and (3) simultaneoulsy, we get
−k1k2k1+k2x=m..x
Thus..x=−(k1k2/k1+k2)mx
Hence the sought time period T=2π√mk1+k2k1k2
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
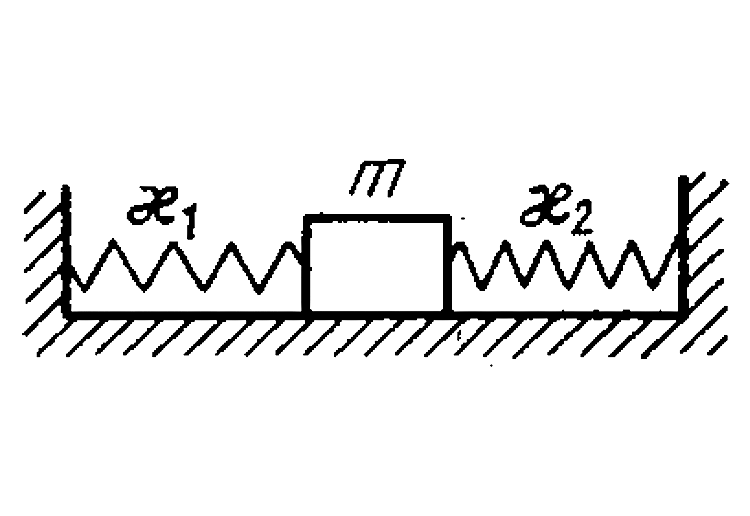
Determine the period of small longitudinal oscillations of a body with mass m in the system shown in figure. The stiffness values of the springs are x1 and x2. The friction and the masses of the springs are negligible.
View SolutionFind the frequency of small oscillatinos of a thin uniform vertical rod of mass m and length l hinged at the point O (figure). The combined stiffness fo the springs is equal to x. The mass of the springs is negligible.
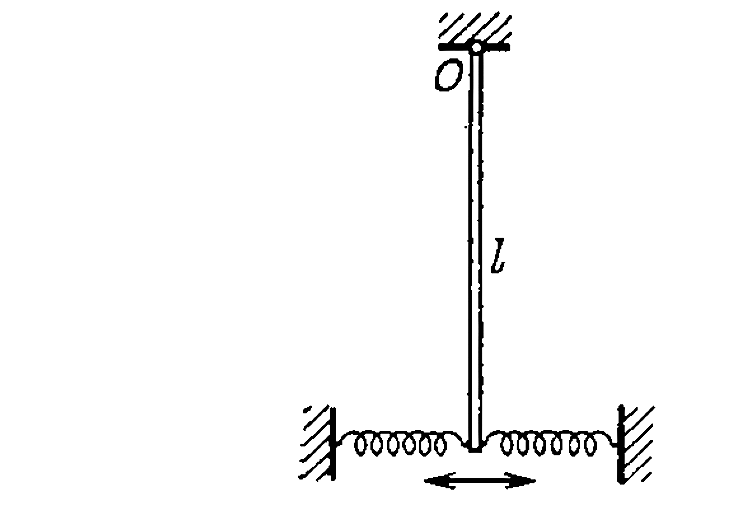
View Solution
Knowledge Check
The time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mKThe frequency of vertical oscillations of the three spring-mass system, shown in figure, is
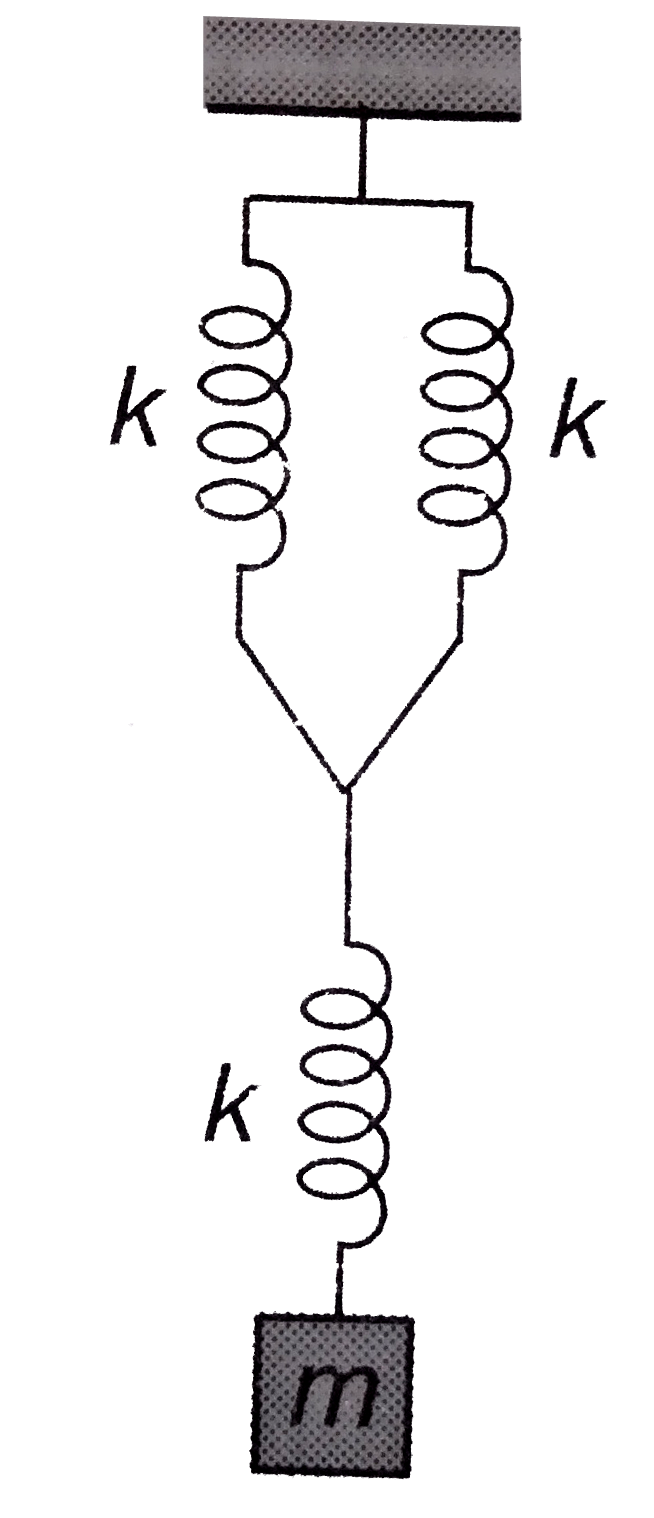 A12π√3k2mB12π√2k3mC12π√2kmD12π√k3m
A12π√3k2mB12π√2k3mC12π√2kmD12π√k3mFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
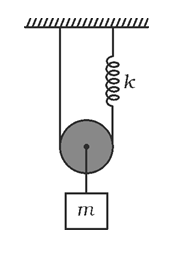 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2k
Find the frequency of small oscillations of the arrangement illustrated in figure. The radius of the pulley is R, its moment of inertia relative to the rotation axis is I, the mass of the body is m, and the spring stiffness is x.The mass of the thread and the spring is negligible , the thread does not slide over the pulley, there is no friction in the axis of the pulley
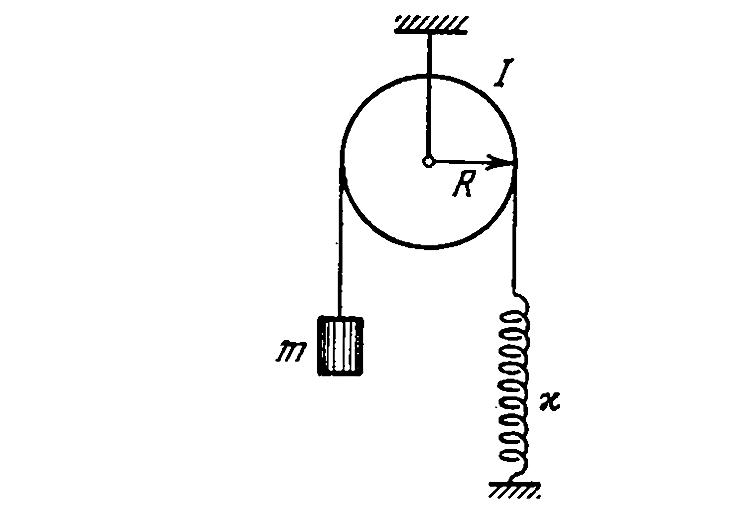
View SolutionFind the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
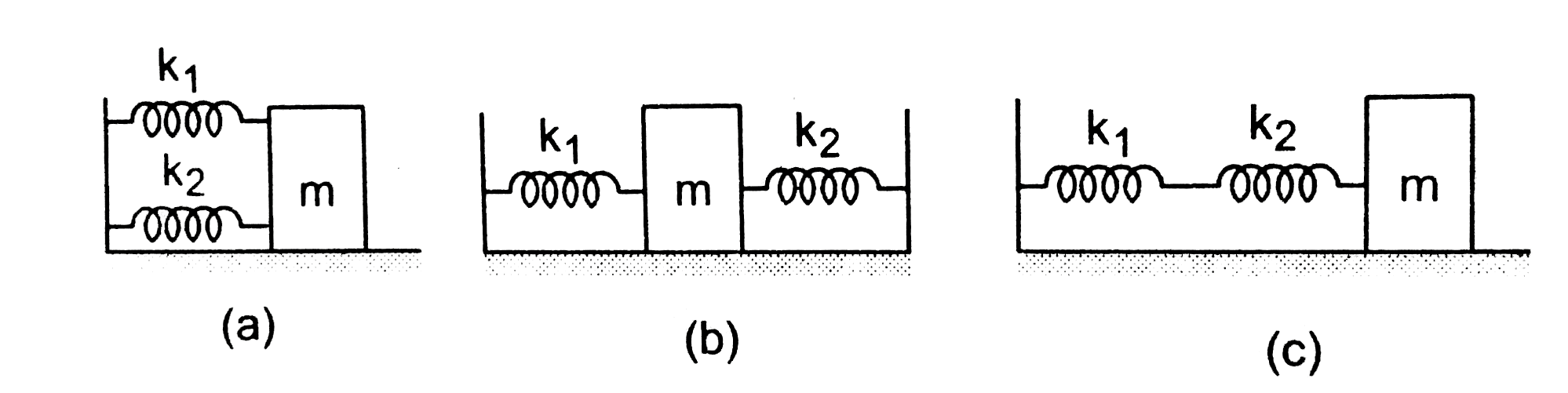
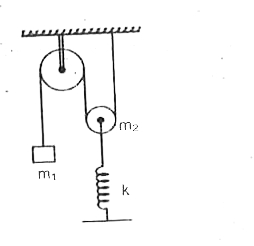
View SolutionThe period of the free oscillations of the system shown here if mass m1 is pulled down a little and force constant of the spring is k and masses of the fixed pulleys are negligible, is
View SolutionA mass suspended on a vertical spring oscillates with a period of 0.5s. When the mass is allowed to hang at rest, the spring is stretched by
View Solution
A thin uniform vertical rod of mass m and length l pivoted at point O is shown is Fig. The combined stiffness of the springs is equal to k. The mass of the spring is negligible. The frequency of small oscillation is .
View Solution
