Find the potential energy of 4-particles, each of mass 1 kg placed at the four vertices of a square of side length 1 m.
+4.0G
7.5G
−5.4G
+6.3G
The correct Answer is:C
To find the potential energy of a system of four particles, each of mass 1 kg placed at the vertices of a square with a side length of 1 m, we can follow these steps:
Step 1: Understand the Configuration
We have four particles, each with a mass of 1 kg, placed at the vertices of a square. The side length of the square is given as 1 m.
Step 2: Identify the Distances
The distances between the particles are crucial for calculating the gravitational potential energy. The distances between adjacent particles (e.g., A and B) is 1 m, while the distances between diagonal particles (e.g., A and C) can be calculated using the Pythagorean theorem.
For a square:
- Distance between adjacent vertices (e.g., A and B): d=1m
- Distance between diagonal vertices (e.g., A and C):
dAC=√(12+12)=√2m
Step 3: Calculate the Number of Unique Pairs
To find the total potential energy, we need to consider all unique pairs of particles. The number of ways to choose 2 particles from 4 is given by the combination formula (nr):
Number of pairs=(42)=4!2!(4−2)!=6
Step 4: Calculate the Gravitational Potential Energy for Each Pair
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
where G is the universal gravitational constant.
For our case:
- For pairs at distance 1 m (4 pairs: AB, BC, CD, DA):
U1=−G⋅1⋅11=−G
Total for these pairs: 4×(−G)=−4G
- For pairs at distance √2 m (2 pairs: AC, BD):
U2=−G⋅1⋅1√2=−G√2
Total for these pairs: 2×(−G√2)=−2G√2=−√2G
Step 5: Combine the Total Potential Energy
Now, we can combine the potential energies from both sets of pairs:
Utotal=−4G−√2G
This can be simplified to:
Utotal=−(4+√2)G
Step 6: Final Result
Thus, the total gravitational potential energy of the system of four particles is:
Utotal=−(4+√2)G
We have four particles, each with a mass of 1 kg, placed at the vertices of a square. The side length of the square is given as 1 m.
The distances between the particles are crucial for calculating the gravitational potential energy. The distances between adjacent particles (e.g., A and B) is 1 m, while the distances between diagonal particles (e.g., A and C) can be calculated using the Pythagorean theorem.
- Distance between adjacent vertices (e.g., A and B): d=1m
- Distance between diagonal vertices (e.g., A and C):
dAC=√(12+12)=√2m
To find the total potential energy, we need to consider all unique pairs of particles. The number of ways to choose 2 particles from 4 is given by the combination formula (nr):
Number of pairs=(42)=4!2!(4−2)!=6
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
where G is the universal gravitational constant.
- For pairs at distance 1 m (4 pairs: AB, BC, CD, DA):
U1=−G⋅1⋅11=−G
Total for these pairs: 4×(−G)=−4G
U2=−G⋅1⋅1√2=−G√2
Total for these pairs: 2×(−G√2)=−2G√2=−√2G
Now, we can combine the potential energies from both sets of pairs:
Utotal=−4G−√2G
This can be simplified to:
Utotal=−(4+√2)G
Thus, the total gravitational potential energy of the system of four particles is:
Utotal=−(4+√2)G
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.5
20 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.6
20 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.3
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
Find the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
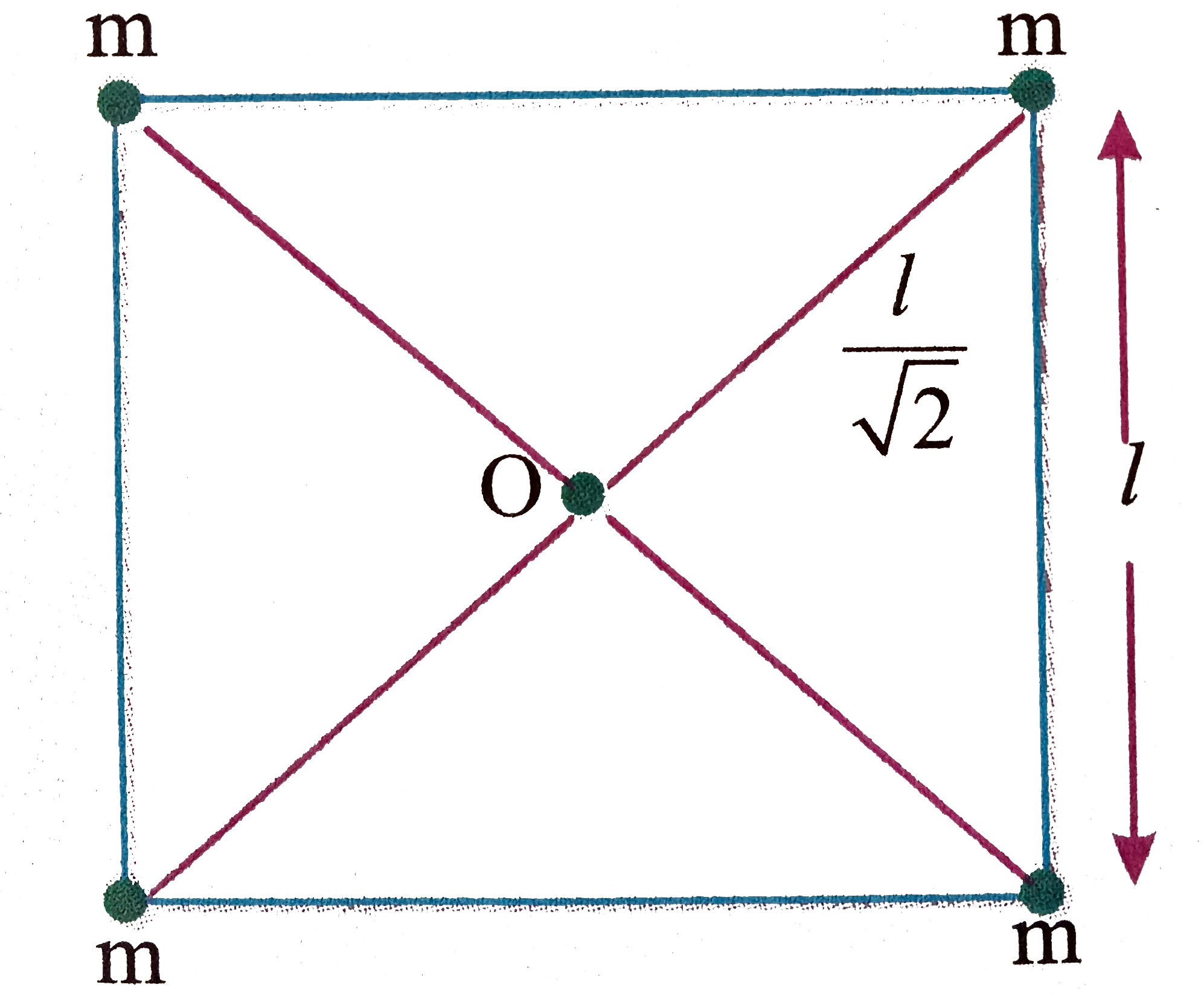
View SolutionFind the potential energy of a system of four particles each of mass 2m kept at the vertices of a square of side x. Also find the potential at the centr of the square.
View Solution
Knowledge Check
Four identical particles each of mass m are arranged at the corners of a square of side length l. If the masses of the particles at the end of a side are doubled, the shift in the centre of mass of the system.
Al6Bl6√2Cl√2Dl5√2Four identical particles each of mass m are arranged at the corners of a square of side length l. If the masses of the particles at the end of a side are doubled, the shift in the centre of mass of the system.
A0.375mB0.25mC0.125mD0.475m
Four identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2 m.If one of the particles is removed,the shift In the centre of mass is
View SolutionFind the potential energy of a system of eight particles placed at the vertices of a cube of side L. neglect the self energy of the particles.
View SolutionFour particles each of mass m are kept at the four vertices of a square of side 'a' . Find gravitational potential energy of this system.
View SolutionFind the work done to bring 4 particle each of mass 100 gram from distances to the vertices of a square of side 20cm.
View SolutionThree identical particles each of mass m are placed at the vertices of an equilateral triangle of side a. Fing the force exerted by this system on a particle P of mass m placed at the

(a) the mid point of a side
(b) centre of the triangle
View SolutionFind the work done to bring 4 particles each of mass 100 gram from large distances to the vertices of square of side 20 cm.
View Solution
