Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
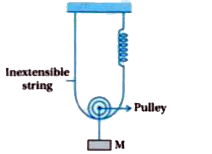 .Solution in Gujrati
.Solution in Gujrati
Here, for calculation of time period we have neglected acceleration of gravity. Because, it is constant at all places and doesn.t affect on resultant restoring force.
Let the equilibrium position, the spring has extended by an amount x0. Let the mass be pulled through a distance x and then released. But, string is inextensible, hence the spring alone will contribute the total extension x+x=2x. So that extension in the spring will be 2x+x0.
When the extension of spring is x0, (M is not suspended) the restoring force in spring.
F=2kx0,.........(1) [∴F=T+T and T=kx0]
When mass is suspended, the net extension in spring 2x+x0 and restoring force in spring,
F.=2k(2x+x0)=4kx+2kx0 ........(2)
Restoring force on system,
f.=−(F.−F)
=F−F.
=2kx0−4kx−2kx0 [From equ. (1) and (2)]
=−4kx
but F=Ma
∴Ma=−4kx
∴a=−4kM⋅k .........(1)
∴a∝−x where, 4kM is constant.
hence, motion of block is SHM
The equation compare to a=−ω2y,
ω2=4kM
∴ω=√4kM
∴2πT=√4kM
∴T=2π2√Mk
∴T=π√Mk or T=2π√M4k.
Topper's Solved these Questions
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-D (NCERT EXEMPLAR SOLUTION LONG ANSWER QUESTIONS)
8 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-E (MCQs ASKED IN GUJARAT BOARD AND COMPETITIVE EXAMS)
66 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-D (NCERT EXEMPLAR SOLUTION VERY SHORT ANSWER QUESTIONS)
10 Videos
- OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE BOOK - KUMAR PRAKASHANCHAPTER - OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE EXERCISE - CHAPTER - 8 (Match Type questions)
5 Videos
- PHYSICAL WORLDBOOK - KUMAR PRAKASHANCHAPTER - PHYSICAL WORLDEXERCISE - SECTION-E (QUESTIONS FROM MODULE)
9 Videos
Similar Questions
A person normally weighing 50kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0s−1 and an amplitude 5.0cm. A weighing machine on the platform gives the persons weight against time.
Will there be any change in weight of the body, during the oscillation?
View SolutionA particle executes SHM along X-axis. The force acting on it is given by……….
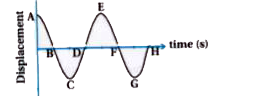
View SolutionDisplacement versus time curve for a particle executing SHM is shown in figure. Idendify the points marked at which (i) velocity of the oscillator is zero, (ii) speed of the oscillator is maximum.
View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere
View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
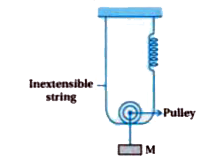
View SolutionFind the time period of mass M when displaced from its equilibrium position and then reelased for the system shown in figure.
View SolutionIn the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is

View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is

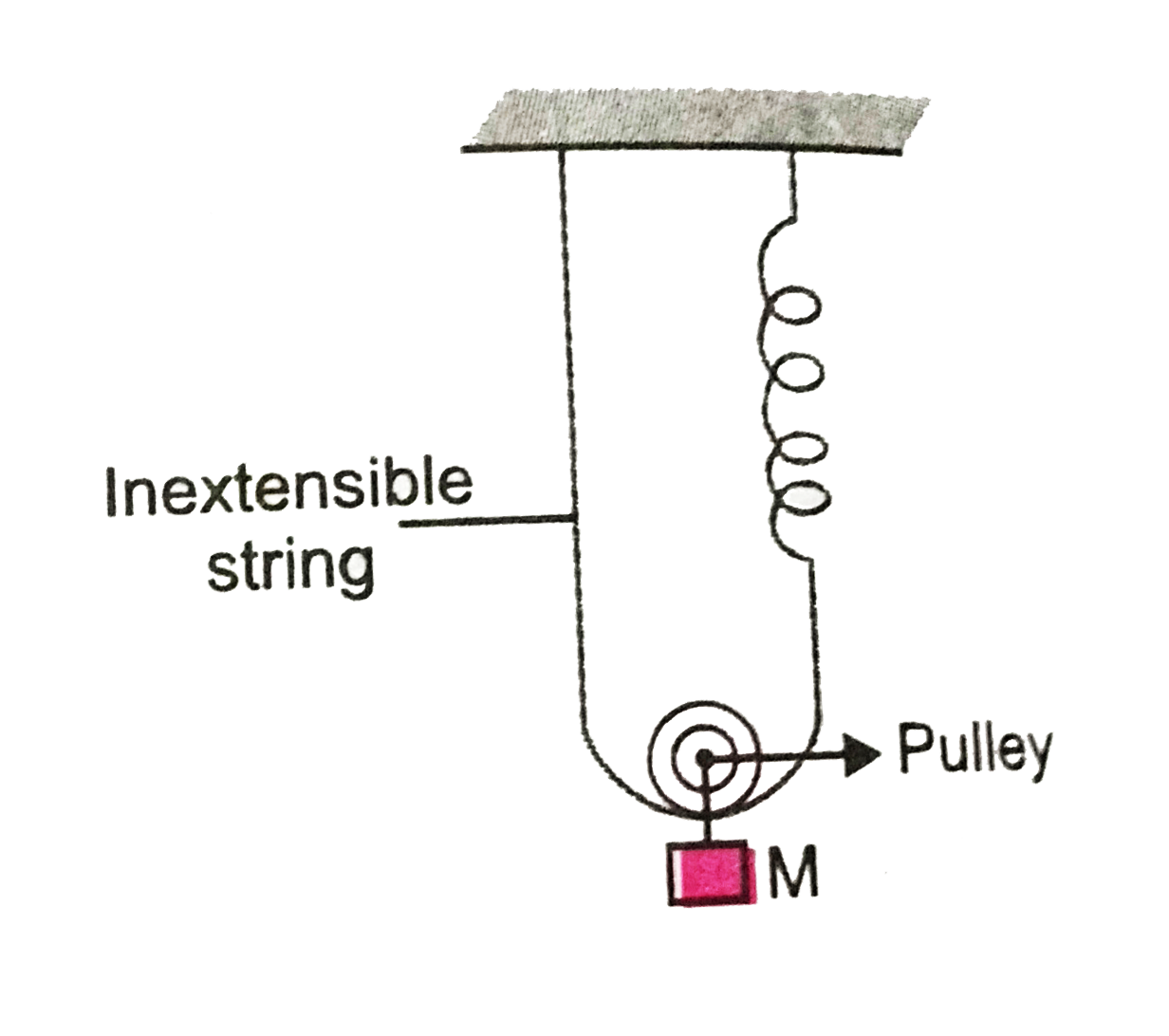
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionConsider the system shown below. If the charge is slightly displaced perpendicular to the wire from its equilibrium position then find out the time period of SHM.
View SolutionTwo springs of spring constant k_(1)and k_(2) are connected by a mass m as shown in the figure. Under negligible friction, if the mass is displaced by small amount x from its equilibrium position and released, the period of oscillation is
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
