Question

Two springs of spring constant $k_1\text{and}{k}_2$ are connected by a mass m as shown in the figure.
Under negligible friction, if the mass is displaced by small amount x from its equilibrium position and released, the period of oscillation is

Options

A. `2pisqrt((m(k_(1)+k_(2)))/(k_(1)k_(2)))`
B. `2pisqrt((m)/(k_(1)+ k_(2)))`
C. `2pisqrt((mk_(1)k_(2))/((k_(1)+k_(2))))`
D. `2pisqrt((m(k_(1)-k_(2)))/(k_(1)k_(2)))`

Answer

B

Explanation

According to question

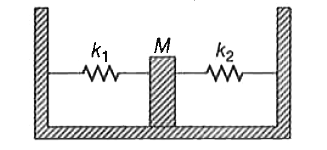
where, `k_(1)` = spring constant for first spring and `k_(2)` = spring constant for second spring.
As, both the spring are in parallel connection, so spring constant equivalent `k_(p)` is
`k_(p) = k_(1) + k_(2)` ...
The time period of oscillation for string mass system is given by
`T = 2pi sqrt((m)/(k_(p)))` ...
From Eqs. (i) and (ii), we get `T = 2pi sqrt((m)/(k_(1)+ k_(2)))`