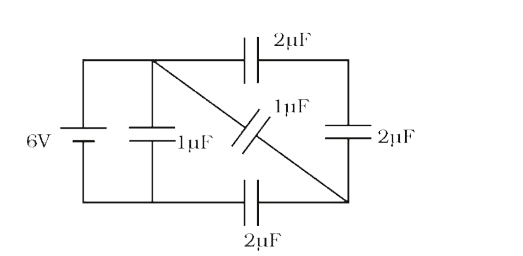
Find the total charge stored in the network of capacitors connected between A and B as shown in figure.
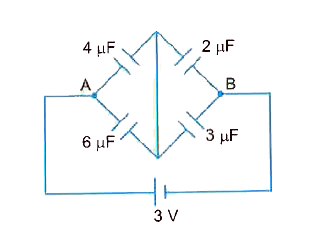
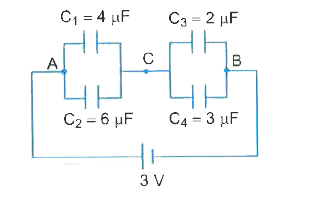
The given network can be redrawn as shown here . The equivalent capacitance of the network is given as :
1C=1(C1+C2)+1(C3+C4)
=1(4+6)μF+1(2+3)μF=(110+15)=310μF
⇒C=103μF
∴ Total charge on the network Q=CV=(103μF)×3V=10μC
Topper's Solved these Questions
- CBSE EXAMINATION PAPER 2020 (SOLVED) BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED) EXERCISE - SECTION - C
7 Videos
- CBSE EXAMINATION PAPER 2020 (SOLVED) BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED) EXERCISE - SECTION - D
6 Videos
- CBSE EXAMINATION PAPER 2020 (SOLVED) BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED) EXERCISE - SECTION - A (Answer the following)
6 Videos
- CBSE EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
11 Videos
- CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
Knowledge Check
Find the total energy stored in capacitors in the network shown in Fig.
 A3.6 × 10 − 5 JB0.6 × 10 − 5 JC5.6 × 10 − 5 JDnone of these
A3.6 × 10 − 5 JB0.6 × 10 − 5 JC5.6 × 10 − 5 JDnone of these
Find the total energy stored in the capacitors in the given network of Fig.
View SolutionFind the charge on the three capacitors shown in figure.
(a)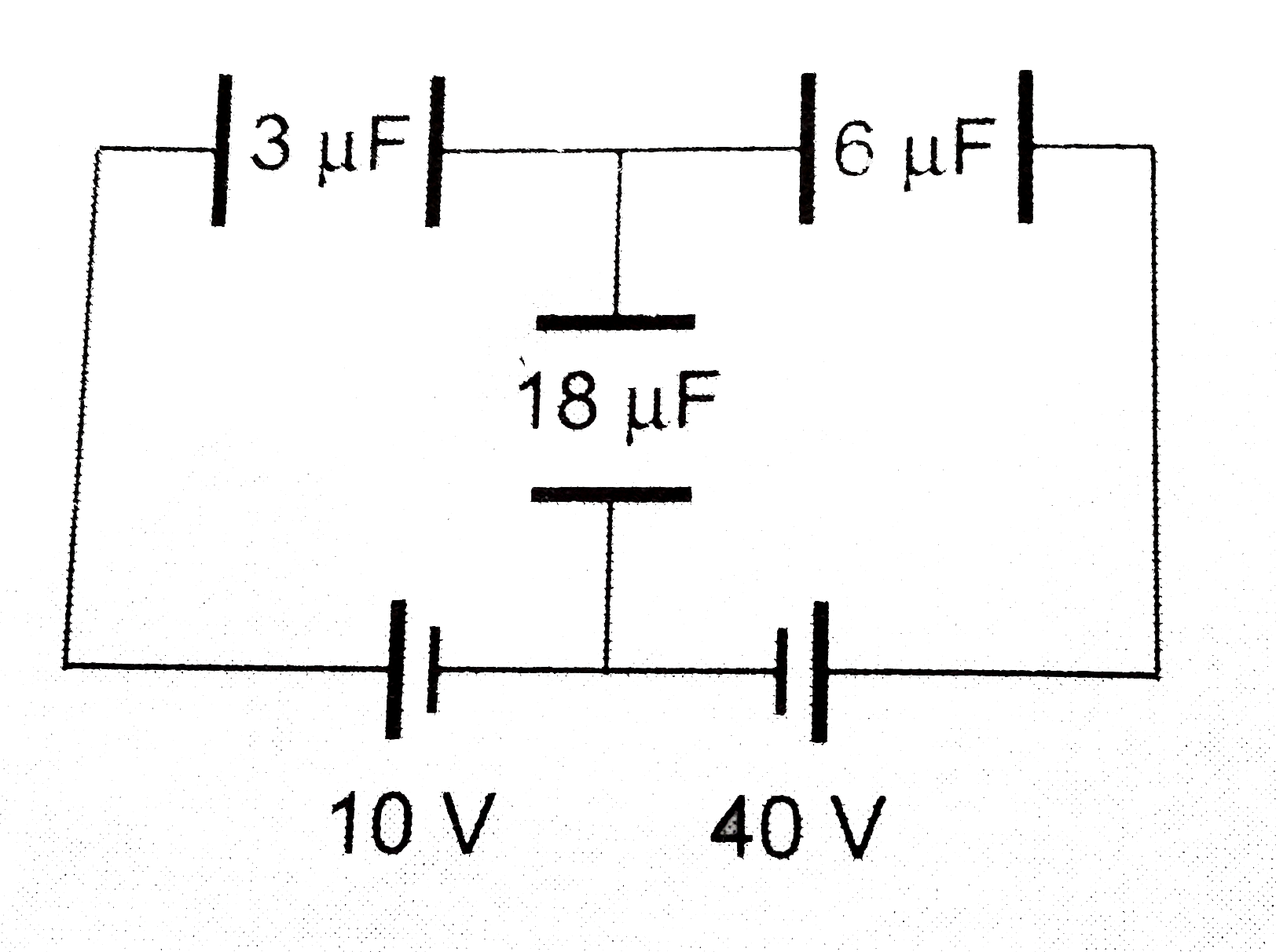
(b)
View SolutionShown in the figure is network of capacitors & resistors. The potentials of some of the nodes are given. Find the
(a) potential of
(b) energy stored in the capacitor connected between R&S
(c) energy stored in the capacitor connected between P&Q

View SolutionShown in the figure is network of capacitors & resistors. The potentials of some of the nodes are given. Find the
(a) potential of
(b) energy stored in the capacitor connected between R&S
(c) energy stored in the capacitor connected between P&Q

View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View Solution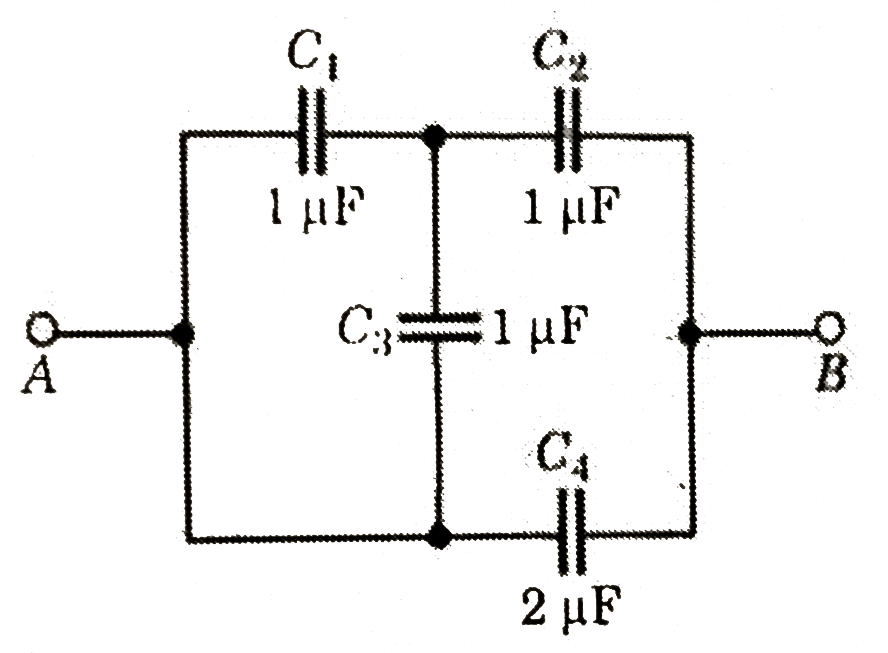
Find the equivalent capacitance between points A and B for the network shown in figure.
View Solution