An infinitely thin straight wire has uniform linear charge density $λ$ . Obtain the expression. For the electric field (E) at a point lying at a distance x from the wire, using Gauss' law.
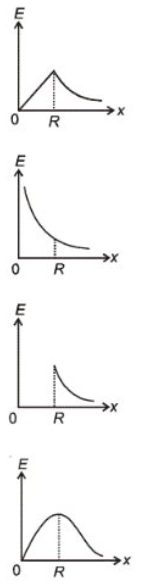
(b) Show graphically the variation of this electric field E as a function of distance x from the wire .

Text Solution

Verified by Experts

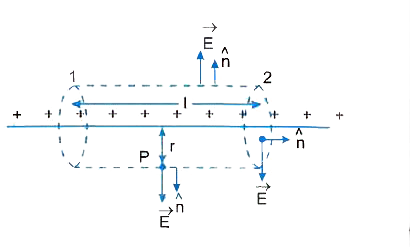
Consider an infinitely long straight charged wire of linear charge density $λ$ . To find electric field at a point P situated at a distance r from the wire by using Gauss. law consider a cylinder of length l and radius r as the Gaussian surface.
From symmetry consideration electric field at eac point of its curved surface is $\to E$ and is pointed outwards normally. Therefore , electric flux over the curved surface.
$= \int \to E . ˆ n d s = E 2 π r l$
On the side faces 1 and 2 of the cylinder normal drawn on the surface is perpendicular to electric field E and hence these surface do not contribute towards the total electric flux.
$∴$ Net electric flux over the entire Gaussian surface $ϕ_{E} = E .2 π r l ... . (i)$
By Gauss law electric flux $ϕ_{E} = \frac{1}{\in_{0}}$ (charge enclosed ) $\frac{λ l}{\in_{0}} ... (i i)$
Comparing (i) and (ii) , we have
$E .2 π r l = \frac{λ l}{\in_{0}}$
$\Rightarrow E = \frac{λ}{2 π \in_{0} r} and \to E = \frac{λ}{2 π \in_{0} r} . ˆ r$
(b) The E - r graph is as shown here.

Updated on:21/07/2023

For a long wire of charge density $γ,$ , field at a distance r from the wire is
A $\frac{γ}{2 π ε_{0} r} n$
B $\frac{γ}{4 π ε_{0} r} n$
C0
D $\frac{k q}{ε^{e}}$
Two infinitely long thin styraight wires having uniform linear charge densities $λ$ and $2 λ$ are arranged parallel to each other at a distance $r$ apart.The intensity of the electric field at a point midway between them is
A $\frac{2 λ}{π ε_{0}}$
B $\frac{λ}{π ε_{0} r}$
C $\frac{λ}{2 π ε_{0} r}$
D $\frac{3 λ}{2 π ε_{0} r}$