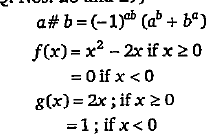Find the value of g'=g(1−2291)1/2
To find the value of g′ given by the formula:
g′=g(1−2291)12
we can follow these steps:
Step 1: Simplify the expression inside the parentheses
We start with the expression:
1−2291
Calculating this gives:
1−2291=291−2291=289291
Step 2: Substitute back into the equation
Now we substitute this back into the equation for g′:
g′=g(289291)12
Step 3: Calculate the square root
Next, we calculate the square root of the fraction:
(289291)12=√289√291=17√291
Step 4: Substitute the square root back into the equation
Now we substitute this back into our equation for g′:
g′=g⋅17√291
Step 5: Final expression
Thus, the final expression for g′ is:
g′=17g√291
This gives us the value of g′ in terms of g.
We start with the expression:
Now we substitute this back into the equation for g′:
Next, we calculate the square root of the fraction:
Now we substitute this back into our equation for g′:
Thus, the final expression for g′ is:
Topper's Solved these Questions
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (2)
7 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (3)
6 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Chapter Practice Test
15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
Similar Questions
Knowledge Check
a#b=(−1)ab(ab+ba)
f(x)=x2−2xifx≥0
=0ifx<0
g(x)=2x,ifx≥0
=1,ifx<0
Find the value of f(g(2#3))+g(f(1#2)):A9401B1049C1094Dnone of these
If G1 and G2 are two geometric means and A is the arithmetic mean inserted two numbers, then the value of G21G2+G22G1 is:
View SolutionIf G be the GM between x and y, then the value of 1G2−x2+1G2−y2 is equal to
View SolutionIf f(a,b)=a+b2
g(a,b)=a2+b2
h(a,b)=max (a,b)
Find the value of f(g(3,9)),h(−1,1)
View SolutionIf a is A.M. of b and c and c,G1,G2,b are in G.P., then find the value of G31+G32−2abc
View SolutionIf A1 and A2 are two A.M.s between a and b and G1 and G2 are two G.M.s between the same numbers then what is the value of A1+A2G1G2
View SolutionIf A1,A2,G1,G2 and H1,H2 be two AMs,GMs and HMs between two quantities then the value of G1G2H1H2 is
View SolutionSuppose f and g are two functions such that f,g: R →R f(x)=ln(1+√1+x2) and g(x)=ln(x+√1+x2) then find the value of xeg(x)f(1x)+g'(x) at x=1
View Solution